SOLO分類理論在高中數學作業批改中的應用*

劉綠芹

近年來，隨著高考競爭壓力的增大，很多學校都非常重視數學訓練，通過大量的作業練習來訓練學生，但教師對學生作業的批改卻成為被忽略的環節。當前作業批改的主要方式是給學生打分數，對學生解答過程的深層次分析和研究很少。因此，我們需要在作業批改中引入一種新方法，不僅要對學生作業進行量化評價，更重要的是進行質性評價，并對學生的思維層次進行劃分，同時展開相應的分析和研究，為學生訂正作業、教師針對性地評講作業打下基礎。

一、什么是SOLO分類理論

SOLO分類理論是一種學生學業評價方法。“SOLO”是英文“Structure of the Observed Learning Outcome”的縮寫，其意為可觀察的學習結果的結構[1]，該理論是一種以等級描述為特征的質性評價方法。香港大學教育心理學教授Biggs，J.B在1982年與Collis，K.F合作出版的《Evaluating the Quality of learning——the SOLO taxonomy》一書中及他在1986年的《The SOLO taxonomy》一文對該理論做了詳細的應用介紹[1]。從國內外的研究發現，SOLO分類理論可以應用到多種學科領域中，包括數學、語文、英語、歷史、生物、化學、地理等，這是SOLO分類理論的優勢所在。

二、SOLO分類理論在高中數學作業批改中的應用舉例

根據SOLO分類理論，我們將學生作業劃分為五個認知水平：前結構水平（P）、單一結構水平（U）、多元結構水平（M）、關聯水平（R）、擴展抽象水平（E）。因此，在作業批改時，我們可以在學生作業的每一道試題上，打上“P、U、M、R、E”這樣的字母符號，對學生的每一道作業做出思維層次水平評價。

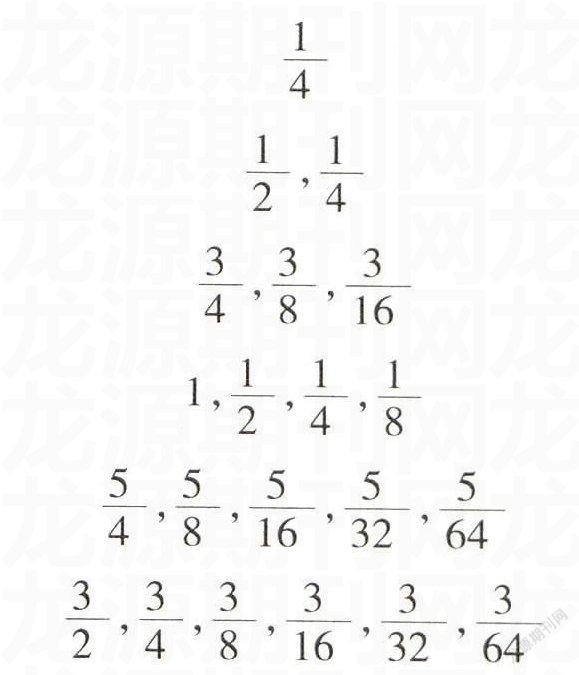
【例】已知一個“三角形數陣”，記第i行第j列的數為aij（i≥j；i，j∈N*）

（1）求a86；

（2）寫出aij關于i，j的表達式；

（3）記第n行……