Zenith Total Delay－Precipitation Water Vapor(ZTD－PWV)全球統計線性關系研究

曾傳俊，劉勁宏

(1.重慶市勘測院，重慶 400020;2.成都市勘察測繪研究院，四川 成都 610000)

1 引 言

水汽在全球的水循環和氣候變化中扮演著關鍵角色?？山邓鸓WV 包含著水汽的時空變化［1］。Askne和Nordius［2］最先推導出大氣濕延遲和可降水汽之間的關系。Bevis 等［3］詳細地推導出了可降水量(PWV)與天頂濕延遲(ZWD)之間的關系，使GPS 技術正式成為水汽探測的一種重要手段。根據文獻［1］和［2］，ZWD 與ZTD、PWV 有如下關系:

式中:∏為轉換系數，ZHD 為天頂靜力學延遲。根據文獻［1］定義，轉換系數∏可表示為:

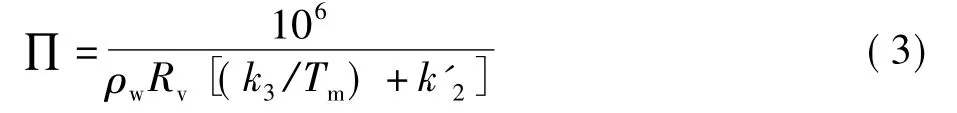
式中ρw為液態水的密度，Rv為水汽氣體常數，k'2、k3為大氣折射常數［4］。

顯然，ZWD 是天頂總延遲(ZTD)減去天頂靜力學延遲(ZHD)得到的。該模型實際上將水汽對ZHD 的影響忽略。其實水汽的分壓對折射率的影響是包含在靜力延遲(ZHD)中的［5］。ZTD 包含著周期變化，與緯度有著強烈的相關性［6］，其變化也能較好反映可降水量變化［7］。因此建立ZTD 與PWV 的直接聯系值得探索，尤其是對于沒有氣象資料的地區，是不能根據ZWD 得到PWV，能夠建立ZTD 與PWV 的關系而不需要額外參數將非常方便且實用。

式中:a，b 為待擬合參數。

本文先利用2005年的ZTD 和PWV 數據探討其線性統計性，然后根據2°×2.5°格網數據進行線性擬合，再與GGOS 和ECMWF 提供的ZWD 和Tm 轉換而來的PWV 進行比較分析。利用2005年的擬合公式，外推2006年，并與2006年的PWV 數據進行統計分析。

2 ZTD 與PWV 的統計線性關系

由于GGOS 和ECMWF 提供的是2°×2.5°格網數據，不能逐個表示出來，因此，本文選2005年的ZTD 和PWV數據，取不同經度下高中低緯度的格網值作為代表進行統計分析。選取格網數據及對應統計圖如表1 所示。

格網數據選取及對應圖示編號 表1

2.1 ZTD 與PWV 的線性統計性

本文采用MATLAB 軟件利用polyfit 函數對PWV進行關于ZTD 的線性擬合，如圖1 所示，紅色為擬合結果。從圖1 上看，(a)、(b)圖偏離較大，PWV 與擬合結果之差的標準差 rms 分別為 3.26 mm 和3.72 mm，(d)、(f)圖擬合效果較好標準差分別為2.51 mm、0.26 mm。圖(c)擬合結果反映了ZTD 的變化趨勢，但標準差rms 較大，3.58 mm，圖e 擬合結果與原始數據并不十分吻合，但標準差較小，2.55 mm。從表1 線性擬合殘差標準差可見ZTD 與PWV 的線性統計性南半球要好于北半球，高緯度地區線性統計性好于低緯度。

圖1 2005年GGOS 和ECMWF 提供的是2°×2.5°格網數據ZTD－PWV 分布圖

2.2 根據ZWD 和Tm 求得PWV 與ECMWF 提供的PWV 的統計性

由ECMWF 提供的ZWD 和Tm 利用式(2)、式(3)求得PWV 與ECMWF 提供的PWV 相比較，如圖2 所示。

圖2 由GGOS 提供的ZWD 和ECMWF 提供的Tm 計算的PWV(紅色)與ECMWF 提供的PWV(藍色)比較

顯然根據ZWD 計算的PWV 具有很好的精度。根據表1，可以發現，高緯度標準差較小，中低緯度標準差較大，南半球標準差較小，而北半球標準差較大。

2.3 PWV 與ZTD 線性相關性分析

PWV 與ZTD 線性相關系數如表2 所示，從表中得知，PWV－ZTD 在緯度60°～－30°范圍內具有很好的相關性。在緯度－60°相關性最低。而在兩極，相關性較差。這與圖1 所示的擬合結果吻合。

格網點相關系數表 表2

本文利用線性擬合值PWV 與ZWD 轉化的PWV之差求得標準差分別a，3.028 7 mm，b，3.389 9 mm，c，2.674 6 mm，d，1.996 0 mm，e，0.586 4 mm，f，0.102 4 mm。與表1 結果對比，發現ZTD－PWV 線性擬合標準差與ZWD－PWV 標準差較小。這說明根據數值預報提供的ZWD 和Tm 計算的PWV 存在模型誤差。ZTD－PWV 線性擬合最大殘差標準差為3.7 mm，精度雖然比ZWD－PWV 較差，但基本能應用于PWV計算，尤其對于沒有氣象數據的地區。

2.4 利用2005年GGOS 與ECMWF 分別提供的2°×2.5°ZTD 和PWV 進行全球擬合

根據前面做的分析，本文繼續對ZTD－PWV 的全球線性相關性進行分析。圖3 為全球ZTD－PWV 的相關性分布圖。

圖3 ZTD－PWV 全球相關性分布圖

從圖3 上可以很清晰地發現，除了圖中赤道周圍三處黃色區域相關性小于0.7 外，在北緯70°到南緯50°范圍內ZTD－PWV 具有很好的相關性，基本在0.8以上。尤其在中國東部，印度和加勒比海，其相關性在0.9 以上，這對于建立區域ZTD－PWV 具有很好的參考價值。

本文根據式(4)分別按格網數據擬合系數a，b。a與b 的全球分布值如圖4 和圖5 所示。

從圖4 和圖5 上看系數a，b 分布具有區域特征，不能建立統一的線性公式。從圖上分布可以發現，在局部地區諸如南極、格陵蘭島、加勒比海、中亞、印度、青藏高原和中國東南部地區系數a，b 變化緩慢，適宜建立區域統一的線性擬合公式。

圖4 系數a 的全球分布圖

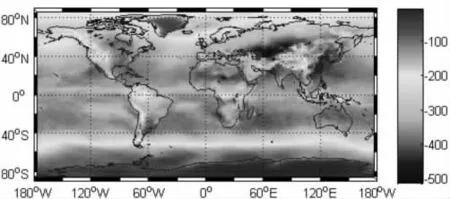
圖5 系數b 的全球分布

圖6 線性擬合標準差(單位:mm)

通過圖6 發現，上述區域標準差小于2.5 mm，特別是青藏高原、格陵蘭島的標準差小于1 mm，而標準差最大不超過6 mm。對于其他相關性很強的區域，應該建立局部線性轉化關系。

2.5 根據2005年數據外推2006年PWV

利用式(4)建立的格網線性公式，根據2006年GGOS提供的ZTD 計算PWV，并與ECMWF 提供的PWV 進行比較。其標準差和相關性如圖7 和圖8 所示。

圖7 2006年數據的標準差

圖8 兩者PWV 之間相關性分布圖

顯然在中低緯度區域，除了赤道，兩者的PWV 相關性超過0.8，標準差小于3 mm，尤其是在中國東南，青藏高原、印度、加勒比海地區相關性超過0.9，標準差小于2 mm。由此可見在某些局部區域可以建立線性公式，進行長期使用。

3 討論與結論

本文利用2005年～2006年GGOS 提供的ZWD 和ZTD 與ECMWF 提供的Tm 和PWV 格網值，對ZTD－PWV 的線性統計性進行了分析，發現在中低緯度區域ZTD－PWV 的線性相關總體在0.8 以上，并且南半球的線性統計性好于北半球的線性統計，在局部地區諸如格陵蘭島、加勒比海、美國東海岸區域、非洲南部、印度、青藏高原和中國東南部線性系數變化緩慢，其相關性大于0.9，適宜建立局部統一線性公式。根據公式外推至2006年，我們發現在上述區域的標準差小于3 mm，區域相關大于0.9。根據ZTD 直接計算PWV的精度比ZWD 轉化PWV 的精度較差，但在無氣象數據區域，根據ZTD 直接計算的PWV 對于氣象學預報也可以提供參考。

［1］Jin，S．G．，and O．F．Luo．Variability and climatology of PWV from global 13－year GPS observations［J］．IEEE Trans．Geosci．Remote Sens，2009，47(7):1918～1924．

［2］Askne J，Nordius H．Estimation oftropospheric delay for microwaves from surface weather data［J］．Radio Sci，1987，22:379～386．

［3］Bevis，M．，Businger，S．，Herring，T．A．，et al．GPS meteorology:remote sensing of atmospheric water vapor using the global positioning system［J］．J．Geophys．Res，1992．(97):15787～15807．

［4］盛裴軒，毛節泰，李建國等．大氣物理學［M］．北京:北京大學出版社，2011．

［5］李成才，毛節泰．地基GPS 遙感大氣水汽總量中的“靜力延遲”和“濕延遲”［J］．大氣科學，2004，28(5)．

［6］Shuanggen Jin ·O．F．Luo·S．Gleason．Characterization of diurnal cycles in ZTD from a decade of global GPS observations［J］．J Geod，2009，83:537 -545．

［7］王勇，劉嚴萍．地基GPS 氣象學原理與應用研究［M］．北京:測繪出版社，2012，44～45．