基于粒子群優化算法的地鐵列車節能運行研究

孫其升 胡文斌 陳 磊 呂建國

(南京理工大學自動化學院，210094，南京//第一作者，碩士研究生)

城市軌道交通的節能研究主要體現在再生制動能量的利用率上［1］。文獻［2-3］在研究動態規劃算法、梯度算法及序列二次規劃算法的基礎上，通過上述算法優化列車的運行速度曲線及儲能設備的充電狀態，仿真結果顯示算法的可行性與有效性;文獻［4-6］主要研究了城市軌道交通列車牽引過程中的惰行控制策略，在單列車牽引仿真的基礎上，采用各種搜索算法，如經典的黃金分割搜索、梯度搜索以及遺傳算法等，尋找惰行位置點，優化列車節能和準時的目標函數;文獻［7-8］在研究地鐵列車單質點模型的基礎上提出多質點模型，使列車運行模型更加符合地鐵列車的實際運行情況;文獻［9］提出了定時約束條件下的列車節能優化操縱模型及算法;文獻［10］在分析列車運行的基礎上致力于列車模擬軟件的研究。

本文在建立地鐵列車運行物理模型的基礎上，采用粒子群優化算法搜尋列車區間運行的惰行點位置，優化列車區間運行時間及區間運行能耗，并利用南京地鐵2號線提供的線路實際參數，對列車區間運行作定時節能策略研究。優化結果顯示，區間運行時間滿足要求的前提下，區間運行能耗大幅下降。

1 列車區間運行狀態力學分析

地鐵列車運行時，運行時分和能耗取決于牽引、制動、勻速和惰行4 種工況的有效分配，對應即形成運行時間最小的節時運行控制策略、運行能耗最小的節能運行控制策略及運行時間與運行能耗綜合最優的定時節能運行控制策略。列車運行狀態示意圖如圖1所示。

列車在區間的運行可以描述為:列車以初速度v0=0 從始發站開始運行，要求在給定時間t 內到達終點站，運行距離為S，運行末速度為vn=0。設列車運行過程中受到的牽引力為Fq，運行阻力為Ff，制動力為Bz，則列車受到的合力為C。其中:列車在起動加速過程中受到的合力為C加=Fq-Ff;制動減速過程中受到的合力為C減=-Bz-Ff;惰行過程中受到的合力為C惰=-Ff。若列車在所受合力作用下的加速度為a，列車運行計算遞推過程如下:

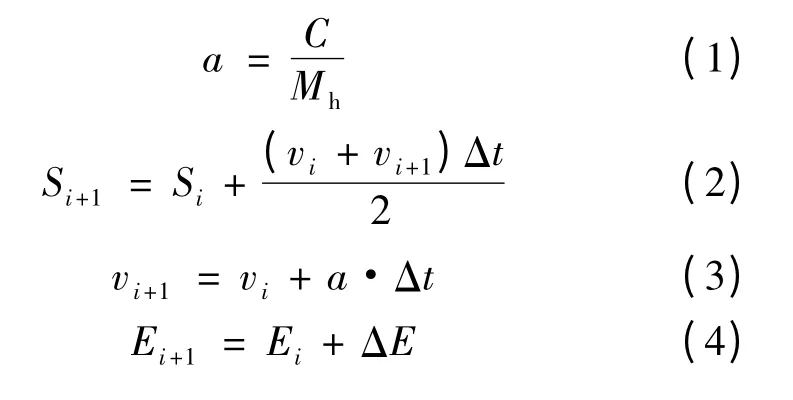
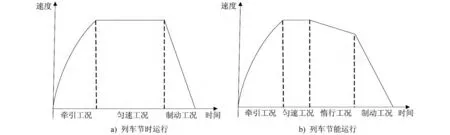
圖1 列車運行狀態示意圖

式中:

Mh——載客列車換算質量，kg;

Si——第i 次計算時列車的運行距離，m;

Si+1——第i + 1 次計算時列車的運行距離，m;

vi——第i 次計算時列車的運行速度，m/s;

vi+1——第i + 1 次計算時列車的運行速度，m/s;

Ei——第i 次計算時列車的運行能耗，kW·h;

Ei+1——第i+1 次計算時列車的運行能耗，kW·h。

2 優化模型

關于列車的定時節能優化，主要方法為:列車在運行過程中采用惰行方式，以節能為優化目標，定時為約束條件，尋找最優的惰行點開始位置和結束位置，保證列車在區間定時、節能運行。

2.1 地鐵列車運行優化模型目標函數

列車在某一運行區間的速度曲線如圖2所示。列車在該區間的運行采用惰行方式控制，有牽引、勻速、惰行、制動4 種工況。既有研究表明:區間運行時間一定時，列車以勻速牽引運行克服的基本阻力功最小;列車以最大加速度加速可減小加速過程中的基本阻力功;列車以最大制動力制動有利于節能;列車制動前惰行以降低制動前運行速度有利于減少列車動能損失［11］。因此，列車從A 站出發后，首先牽引運行至最大速度，然后勻速運行至D1開始惰行，運行至D2停止惰行開始制動，到B 站停車。圖中列車只有1 次惰行，實際運行列車可采用多次惰行過程。列車定時節能優化的問題即轉化為:列車運行時間變化滿足要求的條件下，尋找惰行點的開始位置Di和結束位置Di+1，實現運行能耗最小。列車實際運行時間與列車最小運行時間之差不超過最小運行時間的8%［9］。

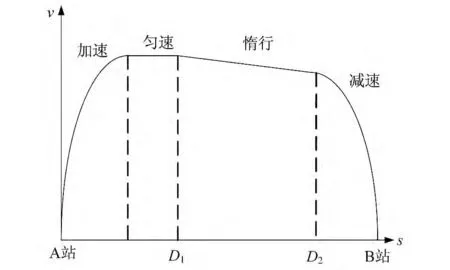
圖2 基于惰行的列車運行速度曲線

保證列車區間運行時間滿足要求的前提下，優化列車運行能耗模型的目標函數為:

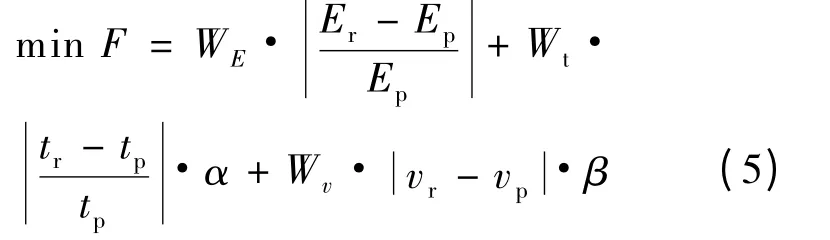
式中:

WE，Wt，Wv——分別為能耗權重系數、時間權重系數和速度權重系數，WE+Wt+Wv=1;

α，β——分別為超時懲罰因子和超速懲罰因子;

tr，tp——分別為實際運行時間和最小運行時間，s;

Er，Ep——分別為實際運行能耗和最小運行能耗，J;

vr，vp——分別為列車實際運行速度和最高運行速度，m/s。

2.2 地鐵列車運行優化模型目標約束

列車從A 站出發在規定的時間內運行至B 站，滿足如下約束條件。

距離約束:

式中:

t——規定的列車運行時間，s;

S——A 站至 B 站的距離，m。

時間約束:

限速約束:

式中:

vi——第i 次計算時列車的運行速度，m/s;

vmax——列車運行限速，m/s。

邊界條件:

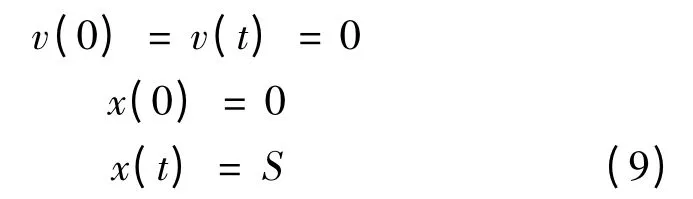
式中:

v(0)，x(0)——分別為列車運行起點速度和位置;

v(t)，x(t)——分別為列車運行終點速度和位置。

惰行點約束:

式中:

Di——第 i 個惰行點位置;

Di+1——第i+1個惰行點位置。

3 模型求解

粒子群算法是研究鳥類個體與群體協作、競爭行為發展起來的具有高度并行、隨機、自適應的搜索算法，特別適用于傳統搜索算法難以求解的非線性約束問題。

應用粒子群算法求解列車運行惰行控制優化模型時，求解之前先要確定適應度函數表達式、尋優代數、群體大小及搜索空間維度等參數。

惰行優化問題就是尋找惰行點位置的問題。惰行開始與結束的位置作為粒子群算法的n 維搜索空間的變量(n 一般小于4)，設定群體規模，隨機生成初始化種群，種群中個體參數要滿足約束條件Di≤Di+1;適應度函數如式(5)所示，尋找最小適應度值;確定個體最好位置及全局最好位置。

算法的基本流程如圖3所示。

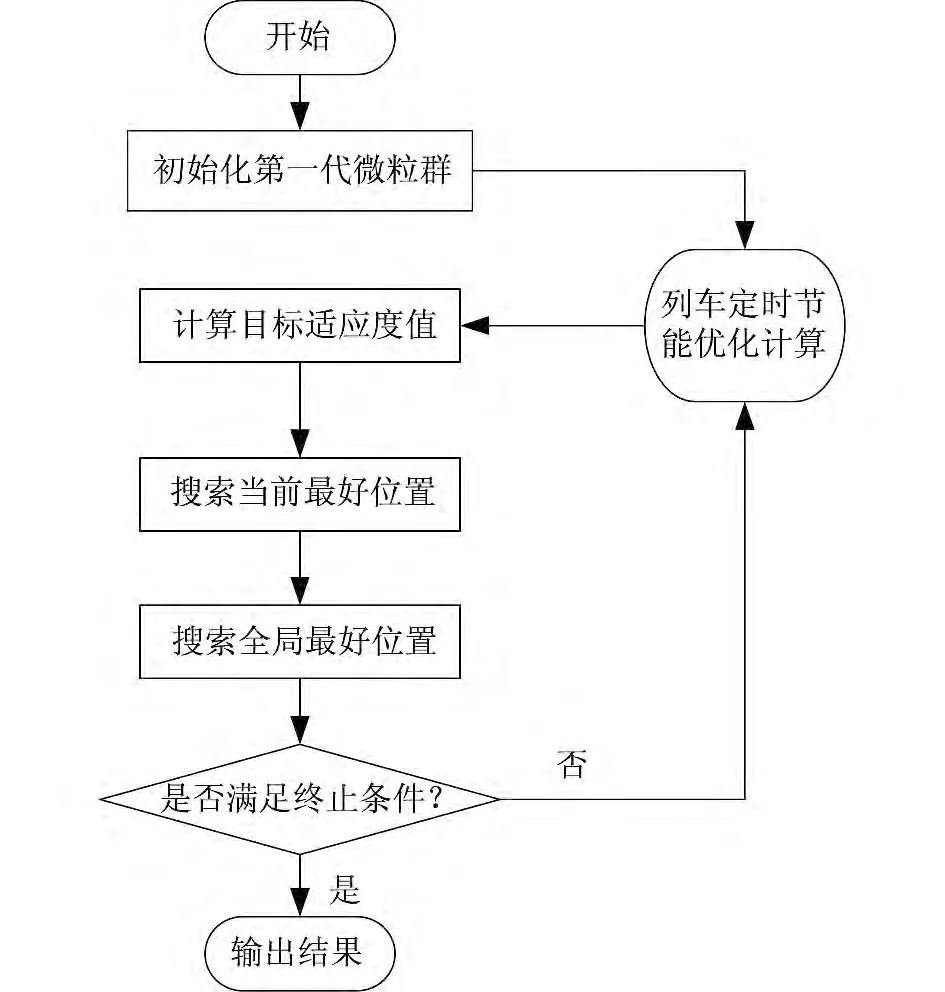
圖3 粒子群算法計算流程

(1)初始化種群，對微粒群中的n 維搜索空間變量{D1，D2，…，Dn}的隨機位置和速度進行初始設定;

(2)依據式(5)定義的適應度函數，計算相應的適應度值;

(3)對于每個n 維搜索空間微粒，將其適應度值與所經歷過的最好位置{Db1，Db2，…，Dbn}的適應度值進行比較，若較好，則將其作為當前的最好位置;

(4)對每個n 維搜索空間微粒，將其適應度值與全局最好位置{Dgb1，Dgb2，…，Dgbn}的適應度值進行比較，若較好，則將其作為當前全局最好位置;

(5)對n 維搜索空間微粒的速度和位置進行進化;

(6)判斷是否滿足程序終止條件，如果滿足則進行步驟(7)，不滿足則返回步驟(2);

(7)輸出結果，輸出每個運行區間的列車能耗和運行時間。

其中，各惰行點數列對應的能耗和運行時間的計算步驟如圖4所示。

(1)設置列車起始點s0和終止點s1，初始化列車惰行點位置值pos［n］;

(2)計算列車的總質量，包括拖車質量、拖車數、動車質量、動車數以及滿載率等;

(3)初始化列車運行的初始狀態，包括列車初速度 v0=0，加速度 a0=0.8 m/s2，初始位置 s0=0，運行時間t0=0，位置標志(ID)為0，列車受電弓電流Inet=0，消耗能量E=0;

(4)進入迭代，不滿足結束條件則進行步驟(5)，滿足條件則結束輸出結果，生成報表，作出列車運行圖;

(5)計算列車運行速度、運行距離;

(6)計算列車運行加速度，加速度的計算需要預先計算列車的牽引力、阻力以及判斷列車運行工況;

(7)計算列車的電壓、電流、功率;

(8)計算列車的消耗能量和回饋能量。

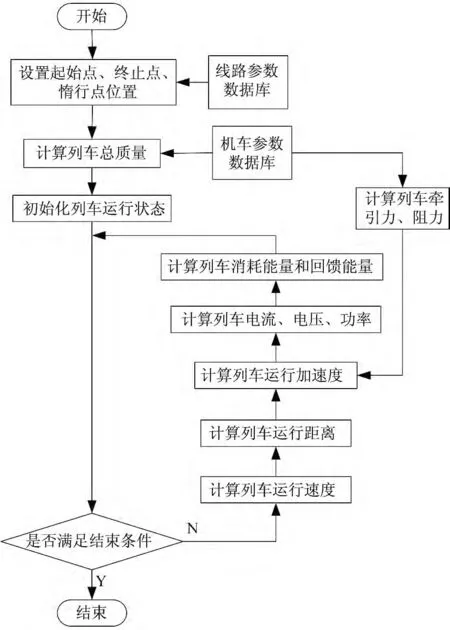
圖4 列車運行狀態計算

4 算例分析

選取南京地鐵2號線莫愁湖—漢中門區段分析列車定時節能優化。待優化區段長995 m。考慮實際線路坡道和彎道，列車限速為70 km/h。列車相關參數見表1。粒子群算法中需要的相關參數見表2。

表3 為南京地鐵2號線莫愁湖—漢中門區段運行仿真及優化結果，其中定時節能模式和定時節能2 模式為采用粒子群算法計算時分別加入了1 次惰行和2 次惰行。三種模式對應的列車運行速度v、距離S、列車受電弓電流I 對于列車區間運行時間t 的波形如圖5所示。由表3 可以看出:①列車采用定時節能模式后，列車的運行時間較節時運行模式增加了3.98 s，能耗減少了6.04 kW·h，饋能減少3.71 kW·h，列車運行時間增加5.5%，列車運行能耗卻降低了18.73%;②莫愁湖—漢中門區段惰行轉換1 次和2 次對于優化結果無影響。

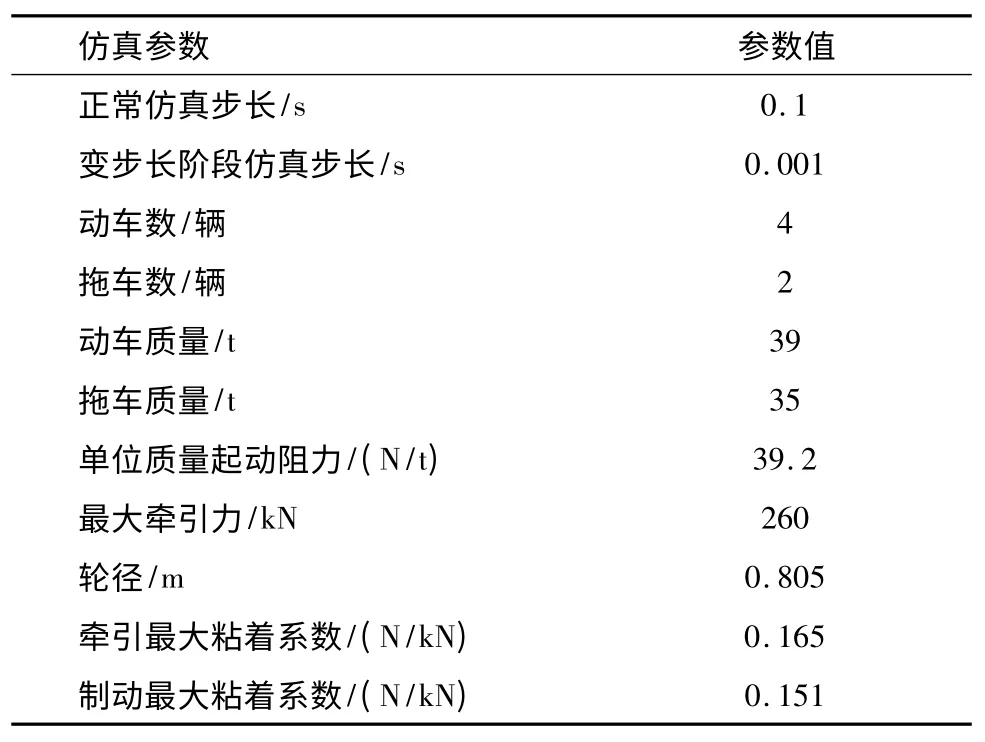
表1 列車相關參數

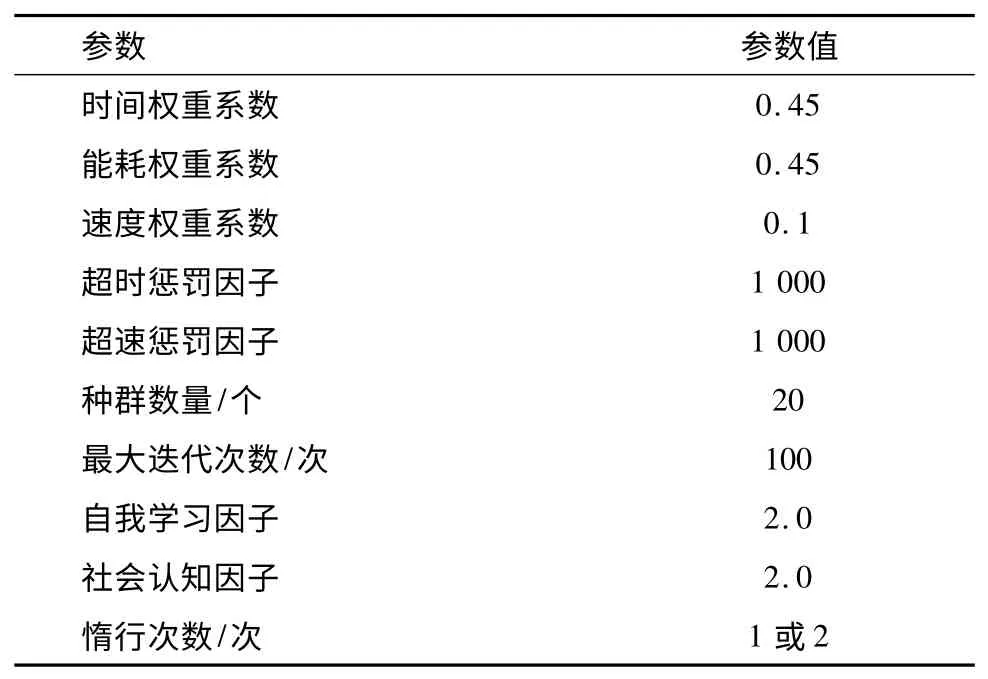
表2 粒子群算法相關參數

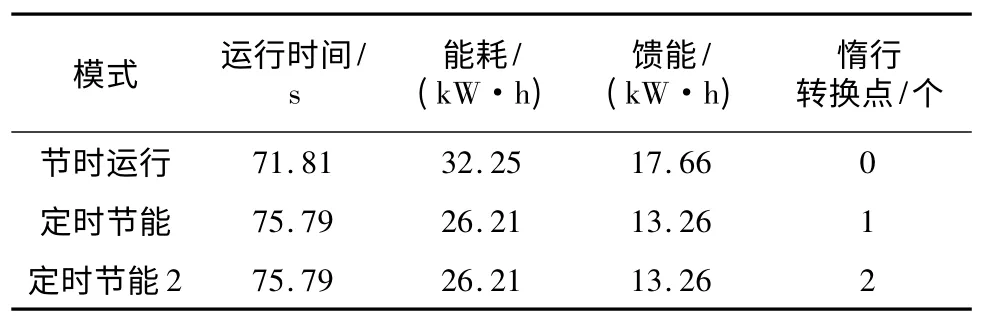
表3 列車在莫愁湖—漢中門區段運行的仿真及優化結果

表4 列出地鐵列車采用粒子群算法優化2 個不同區間惰行點的開始與結束位置的結果。其中莫愁湖—漢中門區間長995 m，馬群—金馬路區間長3 021 m。從表中可見:莫愁湖—漢中門區間采用2次惰行時，2 次惰行節點位置相近，近似于1 次惰行;而馬群—金馬路區間2 次惰行節點區別明顯，且2 次惰行和1 次惰行相比運行時間增加了0.42 s，能耗減少了0.6 kW·h。因此，列車運行模式選擇應根據運行區間長度及運行線路坡道和彎道情況加以確定。

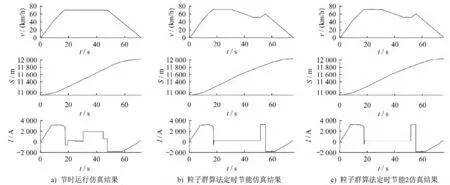
圖5 莫愁湖—漢中門區段運行的仿真及優化結果

南京地鐵2號線全區間優化前和優化后的列車運行速度曲線如圖6所示。由圖可見:區間長度小于1 km 時，采用1 次惰行;區間長度大于2.5 km時，采用2 次惰行;區間長度在兩者之間時，根據實際線路情況決定。

表4 不同區段運行優化后惰行點位置

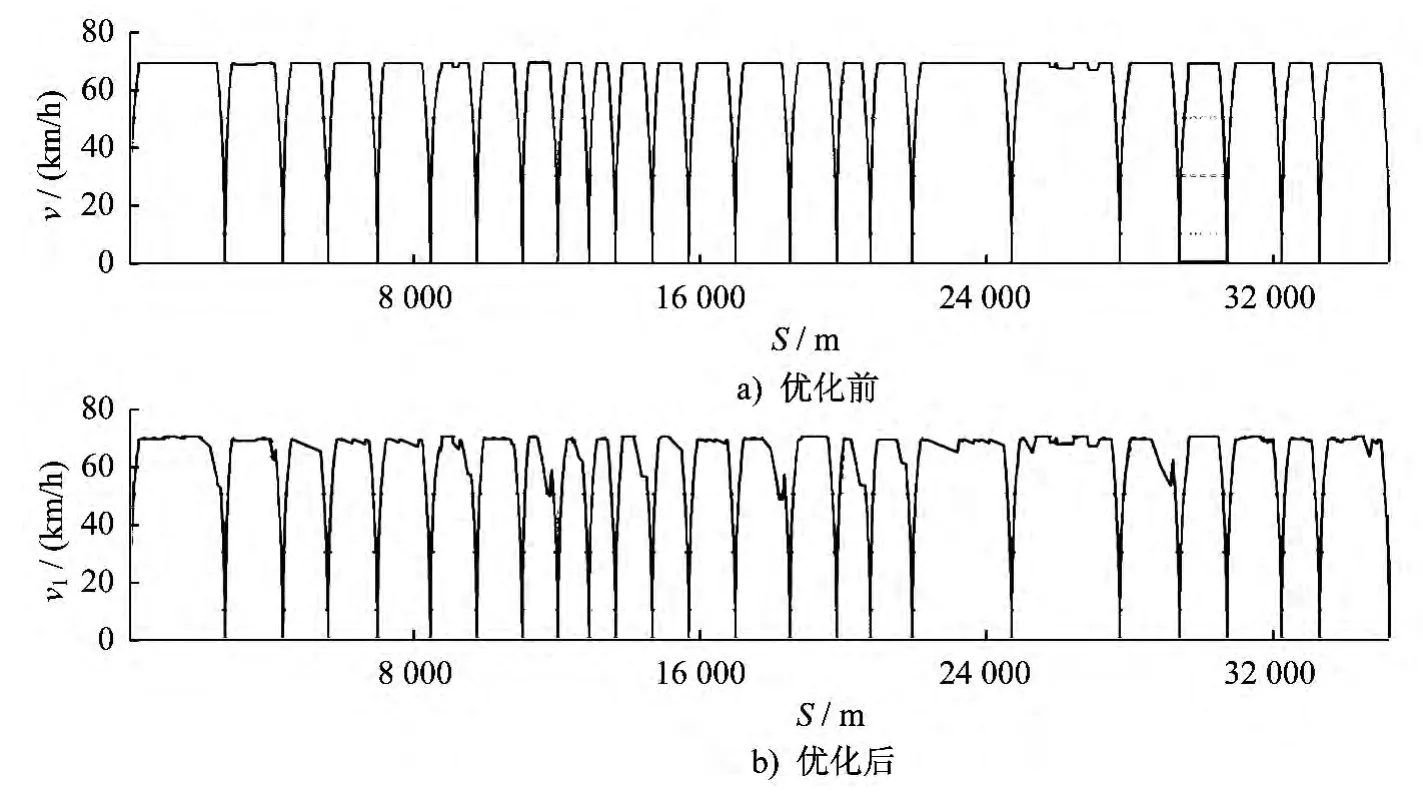
圖6 列車運行全區間速度-距離曲線

5 結 語

本文在國內外研究成果的基礎上，結合南京地鐵2號線列車運行的基本參數，利用粒子群算法搜尋列車區間運行的惰行點位置，仿真分析南京地鐵2號線實際線路區段優化前和優化后列車運行v-t、S-t、I-t 曲線，比較各區段列車運行時間及運行能耗，得出結論:粒子群算法可滿足定時節能的優化要求，且區間運行時間增加5.5%，列車運行能耗相應降低18.73%。本文優化前后列車最大運行速度不變，如果實際列車運行限速提升10%，節能空間將進一步提升。

［1］Gunselmann W.Technologies for increased energy efficiency in railway systems［C］//Power Electronics and Applications，2005 European Conference on IEEE，2005(10):10.

［2］Miyatake M，Ko H.Optimization of train speed profile for minimimum energy consumption ［J］.IEEJ Transactions on Electric Engineering，2010，5(3):1.

［3］Miyatake M，Matsuda K.Energy saving speed and charge/discharge control of a railway vehicle with on ‐ board energy storage by means of an optimization model［J］.IEEJ Transactions on Electrical and Electronic Engineering，2009，4(6):771.

［4］Wong K K，Ho T K.Dynamic coast control of train movement with genetic algorithm［J］.International Journey of Systems Science，2004，35(13-14):835.

［5］Wong K K，Ho T K.Coast control for mass rapid transit railway with searching methods［J］.IET Electric Power Applications，2004(3):365.

［6］Wong K K，Ho T K.Dwell-time and run-time control for DC mass rapid transit railway ［J］.IET Electric Power Applications，2007(6):956.

［7］石紅國.城市軌道交通牽引計算算法［J］.交通運輸工程學報，2004，4(3)，30.

［8］石紅國.城市軌道交通牽引計算模型［J］.交通運輸工程學報，2005，5(4)，20.

［9］丁勇，劉海東，栢赟，等.地鐵列車節能運行的兩階段優化模型算法研究［J］.交通運輸系統工程與信息，2011，11(1)，96.

［10］毛保華.列車運行計算與設計［M］.北京:人民交通出版社，2010.

［11］錢立新.世界高速鐵路技術［M］.北京:中國鐵道出版社，2003.