解多項式雙層規劃最優解的參數化方法
徐俊彥,苗 壯,劉慶懷
(長春工業大學基礎科學學院,吉林長春130012)
解多項式雙層規劃最優解的參數化方法
徐俊彥,苗 壯,劉慶懷
(長春工業大學基礎科學學院,吉林長春130012)
給出解多項式雙層規劃最優解的參數化算法.以上層變量為參數,對雙層規劃下層利用參數化方法求解;得到合理反應集代入上層,使雙層問題轉化為多項式規劃求解.證明了算法的收斂性,數值例子表明算法是可行的.
全局優化;多項式雙層規劃;非孤立最優解
1 預備知識
最早雙層規劃是H.V.Stackelberg在研究經濟問題時提出的,20世紀70年代作為優化問題進行研究.如文獻[1-4]給出了求最優解的一些結論.文獻[5-8]提出了基于參數規劃理論和轉化技術的算法.本文給出上層目標及約束函數都是非凸多項式的雙層規劃算法,該算法融入了非孤立最優解的思想,克服了現有一些算法有時得到的解為不可行解,甚至遠離全局最優解的問題.
本文考慮如下多項式雙層規劃問題(Polynomial Bileverl Programming Problems):
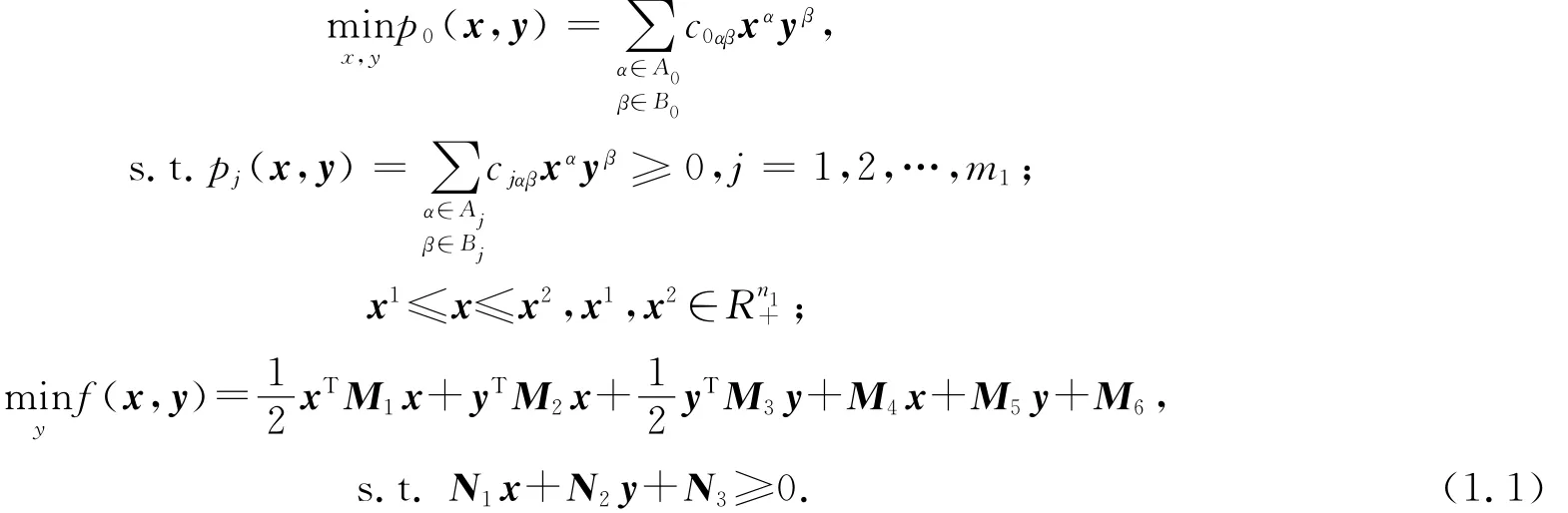
其中:α=(α1,…,αn1),β=(β1,…,βn2)為非負整數向量j=1,…,m1,M6∈R;[M1]n1×n1,[M2]n2×n1,[M3]n2×n2,[M4]1×n1,[M5]1×n2,[N1]m2×n1,[N2]m2×n2,[N3]m2×1為實矩陣,且[M3]n2×n2是對稱正定陣.
2 等價問題
考慮下層問題,x為參數作變換
下層問題轉化為參數二次規劃問題:

其中:
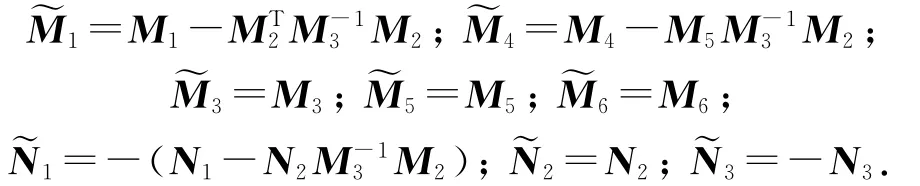
由文獻[9]的結論,下層問題為可解的.對問題(2.2)采用參數規劃算法求解[10],得到合理反應集
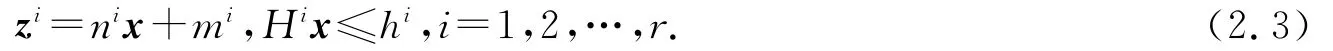
將(2.3)式與(2.1)式代入(1.1)式的上層得:
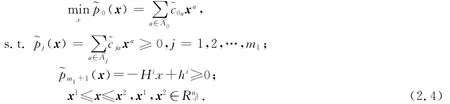
其中α=(α1,…,αn1)為非負整數向量,~c0α,~cjα∈R,j=1,…,m1.
多項式雙層規劃問題(1.1)被轉化為r個多項式規劃問題(2.4).根據文獻[9]的結論,問題(1.1)有全局最優解.問題(2.4)最優解中最小的為(1.1)的全局最優解.多項式可分解為兩個正系數多項式之差,即
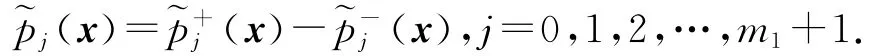
由x1≤x≤x2,x1,x2∈,有
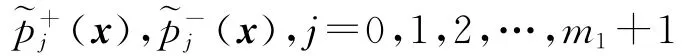
都是增函數.問題(2.4)與問題(2.5)等價.
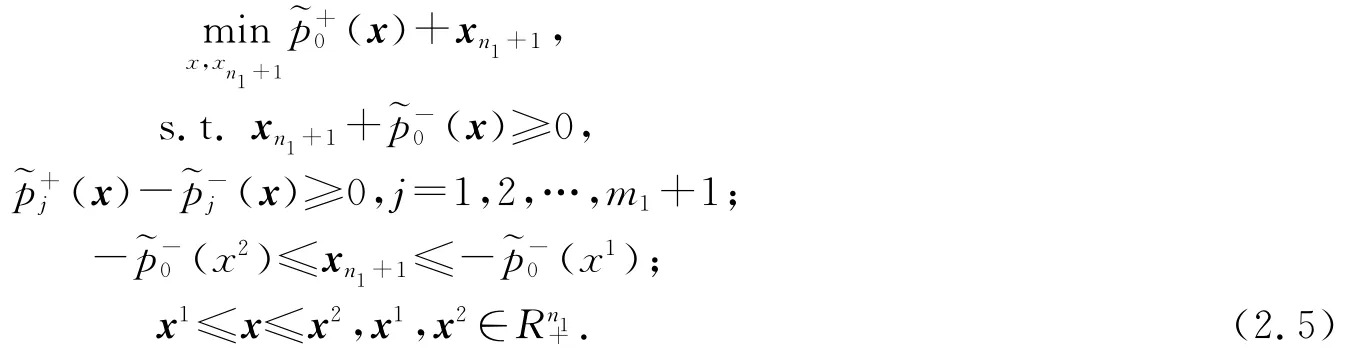
記
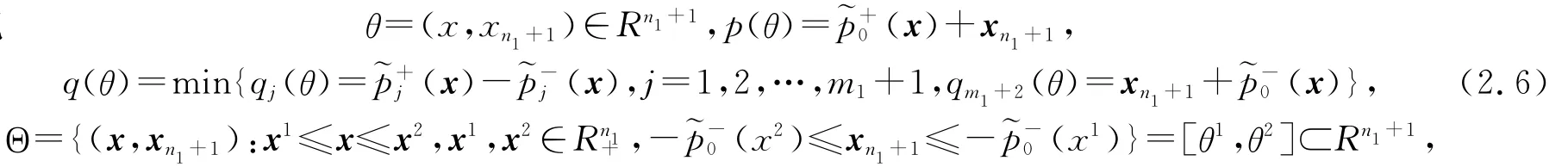
則問題(2.5)表示為問題(FP)

顯然,p(θ)為多項式增函數,且所有系數都是正數;而qj(θ)可分解為兩個多項式增函數uj(θ)與vj(θ)的差,即
3 算法及其收斂性
設θ*是問題(FP)的非孤立可行解,對問題(FP)的任意非孤立可行解θ,如果p(θ*)=min{p(θ):θ∈S*},則稱θ*是問題(FP)的非孤立最優解(其中S*為問題(FP)的所有非孤立可行解集).為求解問題,文中作如下假設:
(H1)D={(x,y)∈Rn1+×Rn2,x1,x2∈Rn1+:pj(x,y)≥0,j=1,2,…,m1,x1≤x≤x2,N1x+N2y+N3≥0}是非空閉集.
(H2)集合{θ∈[θ1,θ2]:q(θ)>0}≠?.
(H3)p(θ1)<ρ-ε,q(θ1)≤0.
對ε≥0,若θ∈[θ1,θ2]滿足q(θ)≥ε,則稱θ為(FP)的ε-非孤立可行解.若ˉθ是(FP)的ε-非孤立可行解,且滿足p(ˉθ)-ε≤inf{p(θ):q(θ)≥ε,θ∈[θ1,θ2]},則稱ˉθ為(FP)的ε-非孤立最優解.
為解問題(FP),考慮輔助問題(EP)
max{q(θ):p(θ)≤ρ-ε,θ∈[θ1,θ2]}.
min(FP)和max(EP)分別表示(FP)和(EP)的最優值.下列定理給出(FP)和(EP)的關系.
定理1 假設(H1),(H2),(H3)成立,那么有下列結論:
(1)若θ0為(EP)任一可行解,且q(θ0)>0,則θ0滿足p(θ0)≤ρ-ε,且θ0是(FP)的非孤立可行解.特別的,若max(EP)>0,則(EP)的最優點θ′滿足p(θ′)≤ρ-ε,且θ′是(FP)的非孤立可行解.
(2)設^θ為(FP)的非孤立可行解,若max(EP)<ε,p(^θ)=ρ,則^θ是(FP)的ε-非孤立最優解;若max(EP)<ε,ρ=p(θ2)+ε,則(FP)不存在非孤立可行解.
證明 (1)根據q(θ1)≤0<q(θ0),有θ0≠θ1,并且任一θ=(1-μ)θ1-μθ0(0≤μ≤1),滿足θ1≤θ≤θ0.當μ→1-,知θ→θ0,有q(θ)>0,所以θ為(FP)的可行解.由于θ0是(EP)的任一可行解,有p(θ0)≤ρ-ε.所以θ0滿足p(θ0)≤ρ-ε,同時θ0是(FP)的非孤立可行解.
(2)如果max(EP)<ε,那么sup{q(θ):p(θ)≤ρ-ε,θ∈[θ1,θ2]}<ε,故任一θ∈[θ1,θ2],且q(θ)≥ε,有p(θ)>ρ-ε=p(^θ)-ε,這表明^θ為(FP)的ε-非孤立最優解.若ρ=p(θ2)+ε,那么{θ∈[θ1,θ2]:q(θ)≥ε}=?,則(FP)非孤立可行解不存在.
3.1 基本操作
(1)將可行集進行矩形拆分,采用最長邊二分法.
(2)不失當前可行解情況下,對拆分集有效縮減.令Θ=[θ1,θ2]為感興趣拆分集.求θ∈[θ1,θ2],滿足p(θ)≤ρ-ε的(FP)非孤立可行解.在集合Dρ∩[θ1,θ2]中求Dρ={θ:p(θ)≤ρ-ε,q(θ)≥0}.用較小矩形[θ′1,θ′2]?[θ1,θ2]代替[θ1,θ2],且Dρ∩[θ′1,θ′2]=Dρ∩[θ1,θ2],滿足該條件的矩形[θ′1,θ′2]記為red[θ1,θ2].利用文獻[4]中的引理可以實現上述目的.
3.2 算法描述
步0 給定收斂精度ε>0.若可行解未知,則令ρ=p(θ2)+ε;否則,令ρ=p(ˉθ),ˉθ是當前最好的非孤立可行解.令Q1={Θ1},Θ1=[θ1,θ2],T1=?,k=1.
步1 對Θ∈Qk,計算redΘ.若redΘ=?,則刪除Θ;若redΘ≠?,則用redΘ代Θ.若redΘ=[θ′1,θ′2],則計算上界V[EP(Θ)],且使V[EP(Θ)]若V[EP(Θ)]<0,則刪除Θ.
步2 令Q′k為步1從Qk計算得到結果的集合;令T′k=Tk∪Q′k.
步3 若Q′k=?,則迭代終止:若ρ=p(ˉθ),則ˉθ為問題(FP)的ε-最優解;若ρ=p(θ2)+ε,則問題(FP)是不可行的.
步4 若Q′k≠?,令[θ1k,θ2k]:=Θk∈argmax{V[EP(Θ)]:Θ?Q′k},V(EP)k=V[EP(Θk)].
步5 若V(EP)k<ε,則迭代終止:若ρ=p(ˉθ),則ˉθ為問題(FP)的ε-非孤立最優解;若ρ=p(θ2)+ε,則問題(FP)是不可行的.
步6 若V(EP)k≥ε,計算τk=max{λ:H(θ1k+λ(θ2k-θ1k))≤ρ-ε},令θk=θ1k+τk(θ2k-θ1k).
(1)若q(θk)>0,則θk為問題(FP)的滿足p(θk)≤ρ-ε的一個新非孤立可行解:若q(θ1k)<0,計算θ1k和θk連線與q(w)=0的交點ˉθk,重賦值ˉθ←ˉθk;否則,重賦值ˉθ←θ1k,轉步7.
(2)若q(θk)≤0,ˉθ不變,轉步7.
步7 將Θk分為兩個矩形.令Qk+1為Θk的矩形集合,Tk+1=T′k\{Θk},賦值k:=k+1,回步1.
3.3 算法收斂性
定理2 上述算法在有限步迭代后終止,或得到問題(FP)的ε-非孤立最優解,或證明問題(FP)是不可行的.
證明 若步3出現,即由Q′k=?知,不存在可行解θ使得p(θ)≤ρ-ε=p(ˉθ)-ε成立,故結論正確.若步5出現,即V(EP)k<ε,則max(EP)<ε,由定理1知結論成立.在步6中,由p(θ1k)≤ρ-ε,存在點θk滿足p(θk)≤ρ-ε;若q(θk)>0,則由定理1,θk是滿足p(θk)≤p(ˉθ)-ε的一個非孤立可行解,證明步(1)結論成立.故下列情形之一出現,結論成立:Q′k=φ,V(EP)k<ε,q(θk)>0.其余步驟顯示,對充分大的k,或步3或步5的情形發生,假設算法迭代是無限的.由于步6(1)每出現一次,當前最好的目標函數值至少下降ε(ε>0),而p(θ)有下界,步6(1)不能無限發生.對充分大k,ˉθ不變,且V(EP)k≥ε時,v
數值例子
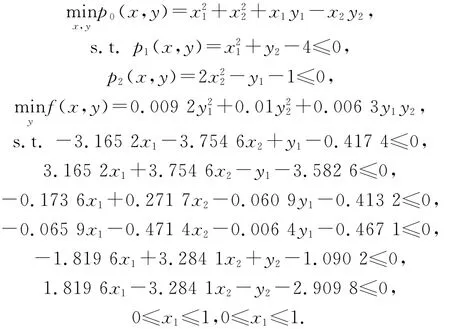
全局最小值點x1=0,x2=0.332,y1=0,y2=-0.000 1.全局最小值為p0=0.220 5,f=0.
[1] CHINCHULUUN A,PARDALOS P M,HUANG H X.Multilevel(hierarchical)optimization:complexity issues,optimality conditions,algorithms.in:advances in applied mathematics and global optimization in honor of gilbert strang[J].Advances in Mechanics and Mathematics Series,2009,17:197-222.
[2] CAO D,CHEN M.Capacitated plant selection in a decentralized manufacturing environment:a bilevel optimization approach[J].Eur J Oper Res,2006,169(1):97-110.
[3] TUY H,MIGDALAS A,HOAI-PHUONG N T.A novel appraoach to Bilevel nonlinear programming[J].J Glob Optim,2007,38(4):527-554.
[4] TUY H,HOAI-PHUONG N T.A robust algorithm for quadratic optimization under quadratic constraints[J].J Glob Optim,2007,37(4):557-569.
[5] NUNO P F,KONSTANTINOS I K,EFSTRATIOS N P.A multi-parametric programming approach for constrained dynamic programming problems[J].Optimization Letters,2008,2(2):267-280.
[6] NUNO P F,PEDRO M S,EFSTRATIOS N P.A multi-parametric programming approach for multilevel hierarchical and decentralised optimisation problems[J].CMS,2009,6(4):377-397.
[7] K?PPE M,QUEYRANNE M,RYANPARAMETRIC C T.Integer programming algorithm for bilevel mixed integer programs[J].J Optim Theory Appl,2010,146(1):137-150.
[8] DEMPE S,MORDUKHOVICH B S,ZEMKOHO A B.Necessary optimality conditions in pessimistic bilevel programming[J].Optimization,2014,63(4):505-533.
[9] VICENTE L.Bilevel programming[D].Coimbra:Department of Mathematics,University of Coimbra,1992.
[10] DUA V,BOZINIS A,PISTIKOPOULOS E N.A multiparametric programming approach for mixed-integer quadratic engineering problems[J].Comput Chem Eng,2002,26:715-733.
Parametric global optimization for polynomial bilevel programming
XU Jun-yan,MIAO Zhuang,LIU Qing-huai
(School of Basic Science,Changchun University of Technology,Changchun 130012,China)
A parametric global optimization algorithm is proposed for solving polynomial bilevel programming problem in this paper.We first describe how we can recast and solve the follower's problem of the bileve fomulation as a multi-parametric programming problem,with parameters being the variables of the leader's problem.By inserting the obtained reasonable response sets in the leader' problem the overall problem is transformed into a set of independent polynomial programming problem.Convergence of the algorithm is established and numerical results are given to show the feasibility.
global optimization;polynomial bilevel programming;nonisolated optimal solution
O 224 [學科代碼] 110·7480
A
(責任編輯:陶 理)
1000-1832(2015)03-0005-04
10.16163/j.cnki.22-1123/n.2015.03.002
2013-12-29
國家自然科學基金資助項目(10771020);吉林省自然科學基金資助項目(20101597).
徐俊彥(1964—),女,碩士,副教授,主要從事最優化理論與算法研究;通訊作者:劉慶懷(1961—),男,博士,教授,主要從事最優化理論與算法研究.

