一類代換系統及其超空間系統
汪 威,李 健,朱曉剛,廖夢蘭,陳冰冰
(1.吉林農業大學信息技術學院,吉林長春130118;2.長春工程技術學院機械系,吉林長春130117;3.吉林大學數學研究所,吉林長春130012)
一類代換系統及其超空間系統
汪 威1,李 健1,朱曉剛2,廖夢蘭3,陳冰冰1
(1.吉林農業大學信息技術學院,吉林長春130118;2.長春工程技術學院機械系,吉林長春130117;3.吉林大學數學研究所,吉林長春130012)
考察了非本原代換及其誘導的集值映射的動力學性質.給出了該類代換誘導的超空間系統是Li-Yorke混沌的一個充分條件.證明了這類代換的拓撲熵為0,并且給出了這類代換誘導的集值映射具有零拓撲熵的一個充分條件.
代換;超空間系統;拓撲熵;Li-Yorke混沌
0 引言
混沌理論的研究涉及很多領域[1].在農業科技研究中,很多實際問題都可以歸結為對混沌現象的分析,如玉米病蟲害的預測預報、農業灌溉用水量的預報、糧食產量的預測等等.本文所涉及的Li-Yorke混沌[2]的定義如下:
設(X,f)為緊致系統,d是X的一個拓撲度量,如果Y?X中任何不同兩點x,y都滿足:
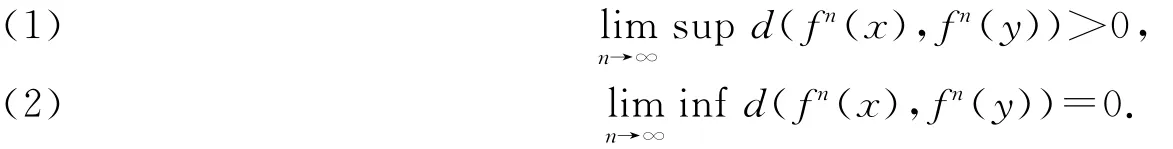
則稱Y為f的Li-York混沌集.如果f有一個不可數的Li-Yorke混沌集,則稱它是Li-Yorke混沌的.
文獻[3]證明了有限個符號的本原等長代換誘導的子移位可能存在Li-Yorke混沌集,但一定不是Li-Yorke混沌的.文獻[4]探討了兩個符號的等長本原代換存在Li-Yorke混沌的等價刻畫.文獻[5]給出了雙符號的非本原等長代換誘導的子移位是Li-Yorke混沌的等價條件.
本文所涉及的有關超空間系統的定義及記號,詳見文獻[6].
設(X,J)是一個拓撲空間,P(x)表示X的所有非空子集構成的集合,G1,G2,…,Gn是X的n個非空開集,令則所有形如B(G1, G2,…,Gn)的集合構成了空間P(x)的某個拓撲的基,這個拓撲稱作Vietoris拓撲.這個拓撲空間記作(P(X),Jv),也稱為(X,J)的超空間.
本文主要考察空間(X,J)的閉集類,即K(X)={K∈P(X);K是X的非空緊子集}.
對任意A,B∈K(X),

其中

而K(X)上與Vietoris拓撲相容的Hausdorff度量定義為
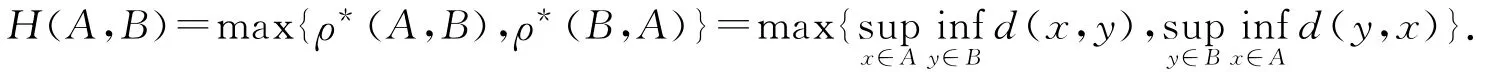
設f:X→X連續.令fˉ:K(X)→K(X)定義為fˉ(A)={f(a):a∈A?X},我們稱fˉ是f到K(X)上的擴張,即fˉ是K(X)上的集值映射.
由文獻[6]可知,空間(K(X),H,fˉ)構成一個緊致系統,稱其為由底空間緊致系統(X,d,f)誘導的超空間緊致系統,簡稱超空間系統,簡記為(K(X),fˉ).底空間緊致系統(X,d,f)簡記為(X,f),稱為底系統.?
1 符號空間和等長代換

則ρ是Σ2上的度量.稱度量空間(Σ2,ρ)為(具有兩個符號的)單邊符號空間,或者稱做符號空間.
定義1.1 設η為符號空間Σ2上的等長代換,定義為
并且滿足條件a0=0,及存在i>0,使得ai=1.則η在Σ2中有一個以0開頭的不動點,記作u.
設Xη為u在移位映射σ作用下軌道的閉包,即
令f=σ|X,則f:Xη→Xη為σ的子移位,稱其為由η誘導的子移位.
定義1.2 如果0?η(1),即η(1)包含0,則稱η是本原的;否則,稱η是非本原的.
下面,我們假設f是由等長代換η誘導的代換子移位,并且給出如下條件:
(C)存在不同的s1,s2,t∈{0,1,…,n-1},使得as1≠bs1,as2≠bs2,并且at=bt.
引理1.1[5]設η是非本原代換,則下述條件等價:
(1)若η滿足條件(C);
(2)f是Li-Yorke的;
(3)f有Li-Yorke對.
以下我們總假設η是非本原的等長代換.(Xη,f)是由η誘導的代換系統子移位,(K(Xη),fˉ)是其誘導的超空間系統.
2 等長代換與Li-Yorke混沌
定理2.1 若η滿足條件(C),則(K(Xη),f )是Li-Yorke混沌的.
證明 由于η滿足條件(C),則由引理1.1可知η是Li-Yorke混沌的,即存在不可數的Li-Yorke混沌集Y?Xη.
任取{x,y}?Y,如果{x,y}是(Xη,f)中的Li-Yorke對,則滿足條件
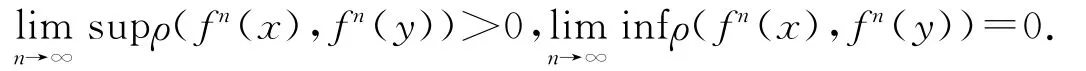
而{{x},{y}}是(K(Xη),fˉ)中的點對,其對應的Hausdorff度量為

于是,對上述{}x,{}y,有
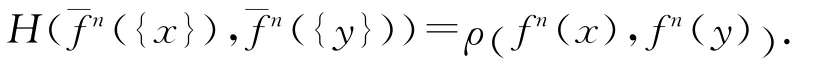
由此可得出如下結論:

即{x}與{y}是(K(Xη),f)中的Li-Yorke點對.
令K(Y)={{x};x∈Y},則K(Y)?K(Xη).根據上述證明可知,K(Y)是(K(Xη),f)的不可數的Li-Yorke混沌集,因此(K(Xη),f)是Li-Yorke混沌的.
3 等長代換與拓撲熵
定理3.1 η誘導的代換子移位的拓撲熵為0,即h(f)=0.
證明 設A為出現在u中的長度為n的符號段,r(A)為A中所含0的個數,則由文獻[5]中斷言3.1及斷言3.2可知
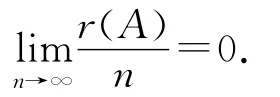
記
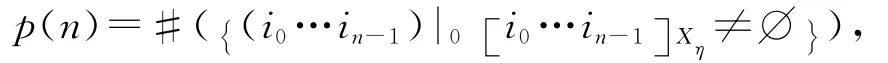
則
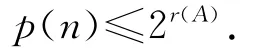
由文獻[7]可知,子系統(xη,f)的拓撲熵
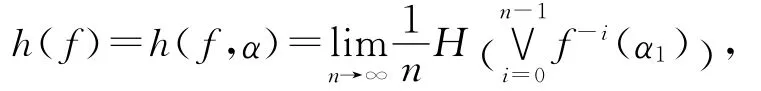
即
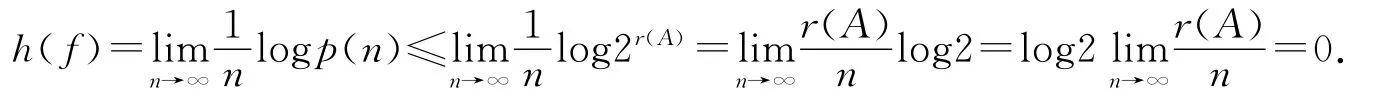
定理3.2 若η不滿足條件(C),則h(fˉ)=0.
證明 由文獻[5]知,若η不滿足條件(C),則Xη中只有兩個點,即v=111…和u=011…,它們都是不動點.因此,K(Xη)={{u},{v},{u,v}}是一個三點構成的離散拓撲空間.進而,fˉ的(n,ε)-張成集和(n,ε)-分離集都是有限集.那么,
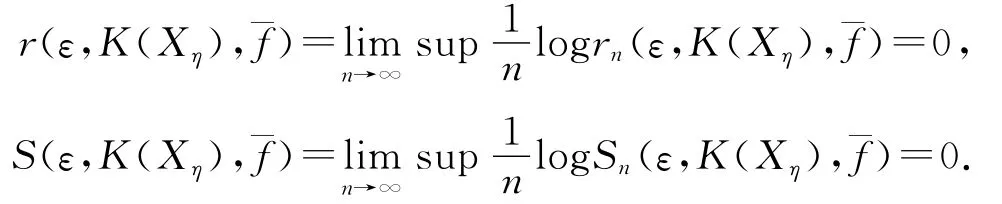
由此可知
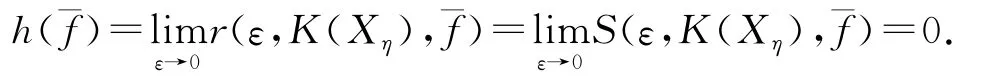
[1] 尹社會,張勇,張付臣,等.基于Lorenz系統的強迫Lorenz混沌系統的動力學研究[J].東北師大學報:自然科學版,2014,46(1):42-47.
[2] LI TIANYAN,YORKE J A.Period three implies chaos[J].The Amer Math Monthly,1975,82:985-992.
[3] BLANCHARD F,DURAND F,MAASS A.Constant-length substitutions and countable scrambled sets[J].Nonlinearity,2004,17:817-833.
[4] 廖公夫,范欽杰,王立冬.一類本原代換與混沌集[J].中國科學:A,2008,38:469-476.
[5] LIAO GONGFU,WANG WEI,FAN QINJIE.A class of non-primitive substitutions and chaos[J].Chinese J Contemp Math,2009,30(2):133-138.
[6] 廖公夫,王立冬,范欽杰.映射迭代與混沌動力系統[M].北京:科學出版社,2013:179-180.
[7] 周作領.符號動力系統[M].上海:上海科技教育出版社,1997:25-27.
A class of substitution systems and the hyperspace systems
WANG Wei1,LI Jian1,ZHU Xiao-gang2,LIAO Meng-lan3,CHEN Bing-bing1
(1.Information Technology College,Jilin Agricultural University,Changchun 130118,China;2.Department of Mechanical Engineering,The Institute of Changchun Engineering Technology,Changchun 130117,China;3.Institute of Mathematics,Jilin University,Changchun 130012,China)
As an important component of nonlinear science,the research on dynamical system has penetrated into many problems of agricultural production,such as prediction of corn yield and research on ecological difference equation.In this paper,we investigated dynamical properties for non-primitive substitution and the set-valued maps induced by the substitution.We gave a sufficient condition for the set-valued maps to be Li-Yorke chaotic,proved that the topological entropy of the substitution is zero,and gave a sufficient condition for the set-valued maps to have 0topological entropy.
substitution;hyperspace system;topological entropy;Li-Yorke chaos
O 189 [學科代碼] 110·31
A
(責任編輯:陶 理)
1000-1832(2015)03-0009-03
10.16163/j.cnki.22-1123/n.2015.03.003
2014-07-07
吉林省科技發展計劃項目(20140204045NY;20130522110JH);吉林省教育廳“十二五”科學技術研究項目(2014第468號);吉林農業大學科研啟動基金資助項目(201310).
汪威(1981—),女,博士,講師,主要從事拓撲動力系統研究.

