帶有非局部時滯的競爭擴散系統的穩定性分析
孫亞男,孟 琳,王 靜
(東北師范大學數學與統計學院,吉林長春130024)
帶有非局部時滯的競爭擴散系統的穩定性分析
孫亞男,孟 琳,王 靜
(東北師范大學數學與統計學院,吉林長春130024)
在齊次Neumann邊界條件下研究了一類具有非局部時滯的競爭擴散系統.利用線性化方法和上下解方法,研究了該系統的局部穩定性和全局穩定性.
競爭系統;反應擴散;平衡點;非局部時滯
1 背景及主要結論
競爭系統是當今生態學研究的熱點問題,由于國內外學者對其研究的深入,極大地推動了該理論的發展.近年來,許多學者對具有擴散項[1-7]或時滯項系統的動力學行為進行了討論,尤其對非局部時滯的研究,獲得了許多成果.對于每一個σ∈[0,∞),核函數Ki(x,y,σ),i=1,2,關于(x,y)∈ˉΩ×ˉΩ都是非負連續的.對于每一個(x,y)∈ˉΩ×ˉΩ,核函數Ki(x,y,σ),i=1,2,關于σ∈[0,∞)都是可測的.由于這個核與時間變量和空間變量均有關,系統(1.1)中的時滯被稱為時空時滯或非局部時滯.文獻[1]研究了具分布時滯的二維Lotka-Volterra競爭擴散系統
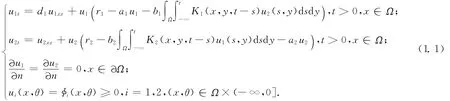
其中:u1(x,t)和u2(x,t)分別表示在位置x和時間t處的種群密度;r1,r2分別表示種群的內稟增長率;a1,a2分別表示種群的內部競爭率;b1,b2表示兩個種群間的競爭率;齊次Neumann邊界條件表示沒有物種跨越邊界Ω;r1,r2,a1,a2,b1,b2是正常數;當(x,θ)∈Ω×(-∞,0]時,初始函數i(x,θ)是非負連續函數.
文獻[2]考慮了一維區域[0,π],在這個區域內時滯項與種群密度u(x,t)有關,并且考慮了時滯項
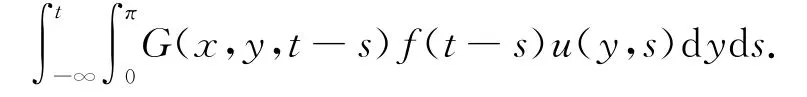
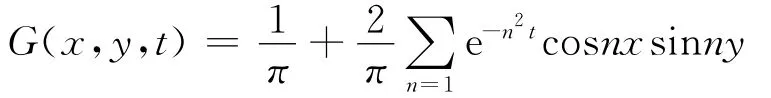
是方程
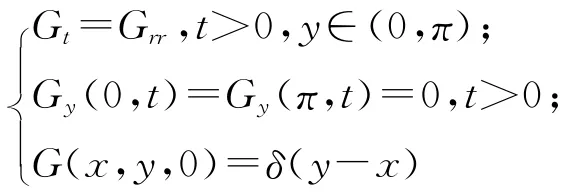
的解.
文獻[3]研究了非局部時滯的具有年齡結構的反應擴散方程
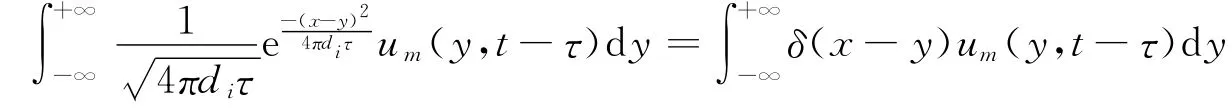
的單調行波解.
文獻[4]研究了
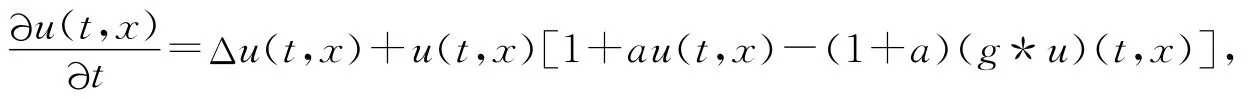
其中
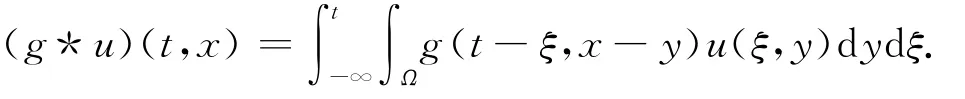
通過建立常微分方程的上下解,并利用單調迭代方法或不動點方法建立了行波解的存在性.文獻[5]研究了具有
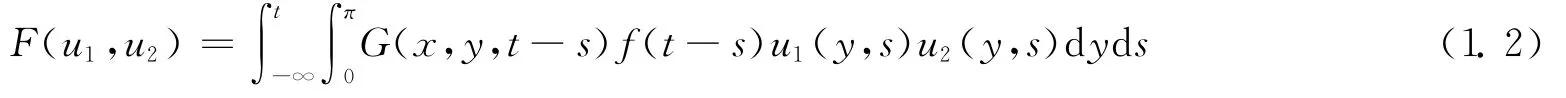
的捕食者-食餌系統的穩定性.這個時滯既與捕食者有關,也與食餌有關.
本文在文獻[5]的基礎上考慮競爭系統
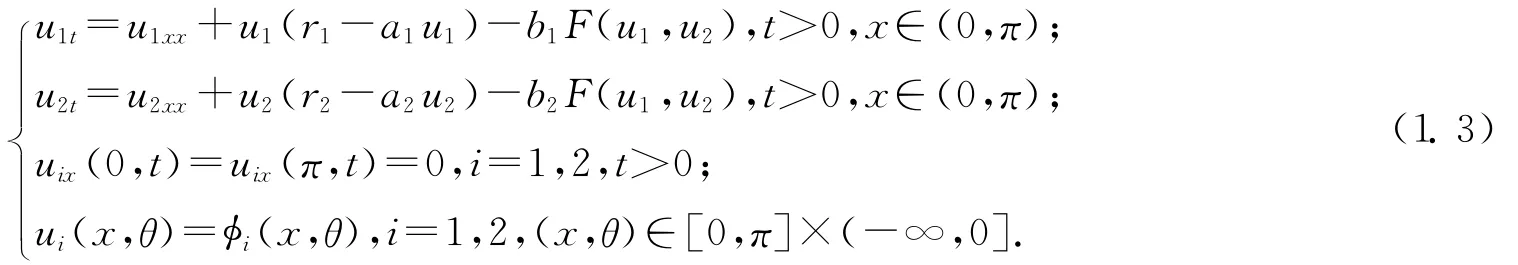
其中
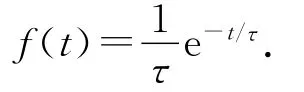
為了下面研究方便,令
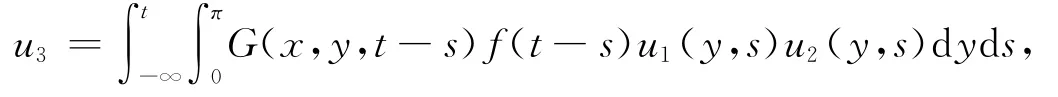
則(1.2),(1.3)式等價于如下問題:
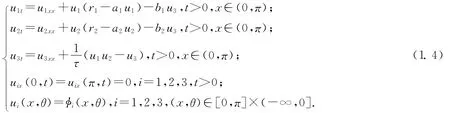
其中1(x,θ),2(x,θ)由(1)式定義,且
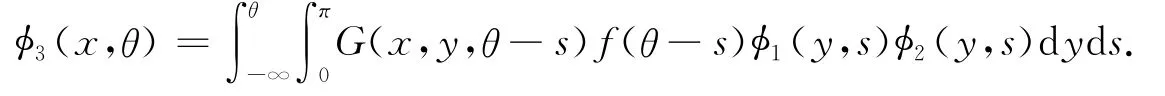
2 常值解的存在性及局部穩定性
通過計算可得系統(1.4)有平凡的常值解E0=(0,0,0)和半平凡常值解為了得到系統(1.4)的正常值解,我們需要給出如下的假設:
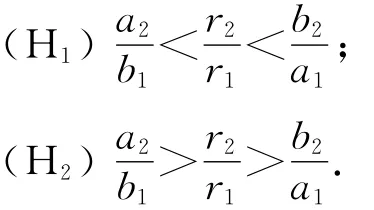
在假設(H1)或(H2)下,顯然系統(1.4)有唯一的正常值解E*=(u*1,u*2,u*3),其中
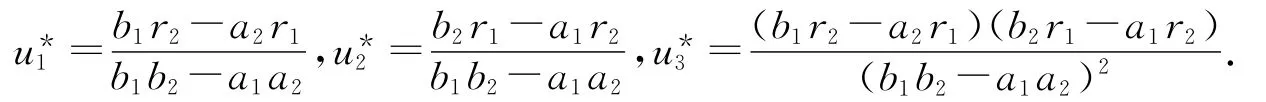
為了證明平衡點穩定性我們引進一些符號.設0=μ1<μ2<…<μn<…是帶有齊次Neumann邊界條件的-Δ算子在(0,π)中的特征值.E(μi)?C1(0,π)表示μi對應的特征子空間.令{ij|j=1,2,…,dimE(μi)}表示E(μ1)的一組正交基,
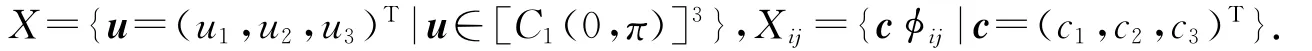
則
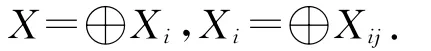
下面把系統(1.4)線性化.令L=IΔu+fu(u),
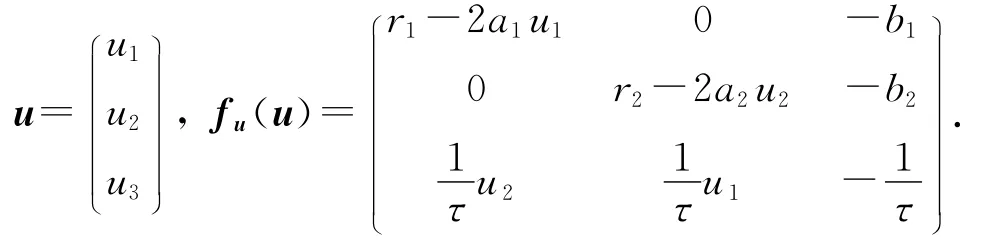
首先給出E0,E1,E2的局部穩定性結果.
定理2.1 對于系統(1.4)有如下特征:
(1)平凡解E0總是不穩定的;
(2)如果b2r1>a1r2且r2τ<r1τ<1,則E1是局部漸進穩定的;
(3)如果b1r2>a2r1且r1τ<r2τ<1,則E2是局部漸進穩定的.
證明 (1)系統(1.4)在E0的線性化系統
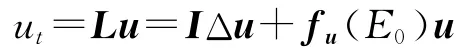
的特征方程是
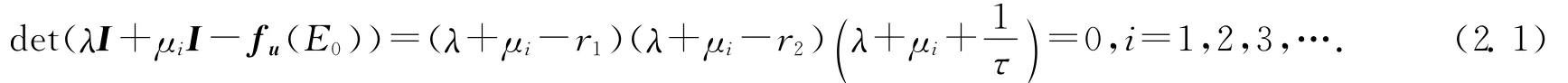
顯然,當i=1時,(2.1)式存在兩個正根λ1=r1>0,λ2=r2>0,于是由于L存在具有正實部的特征根,所以系統(1.4)的平凡解E0不穩定.
(2)系統(1.4)在E1的線性化方程
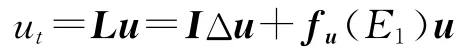
的特征方程為
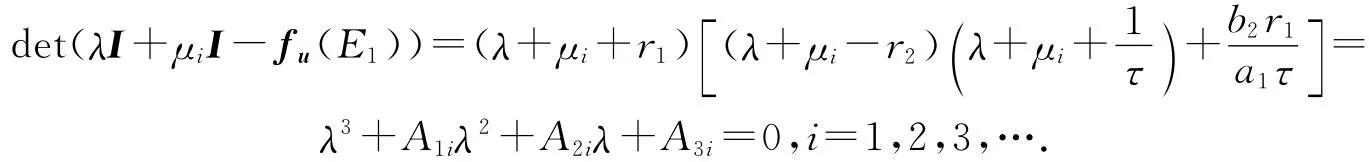
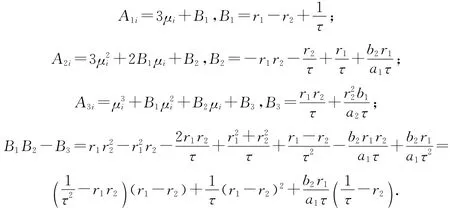
其中:顯然,當b2r1>a1r2,r2τ<r1τ<1時,B1,B2,B3,B1B2-B3都是大于0的,根據Routh-Hurwitz判別法,特征多項式的特征值具有負實部,所以E1是局部漸進穩定的.
(3)系統(1.4)在E2的線性化方程ut=Lu=IΔu+fu(E2)u的特征方程為
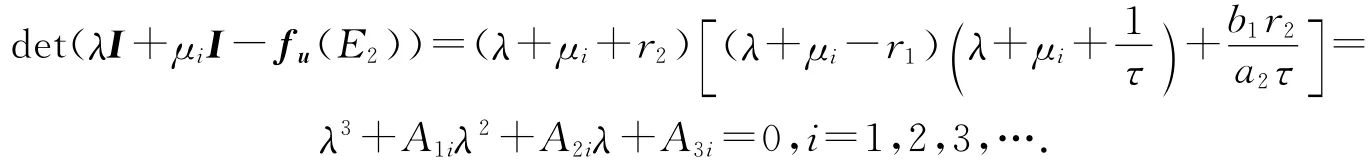
其中:
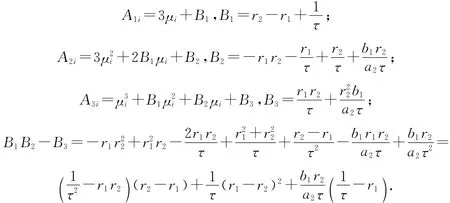
顯然,當b1r2>a2r1且r1τ<r2τ<1時,B1,B2,B3,B1B2-B3都是大于0的,根據Routh-Hurwitz判別法,特征多項式的特征值具有負實部,所以E2是局部漸進穩定的.證畢.
定理2.2 如果假設(H2)成立,并且a1,a2,b1,b2,r1,r2滿足統(1.4)的正常值解E*是局部漸進穩定的.
線性化方程
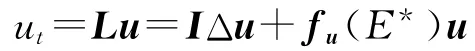
的特征方程為
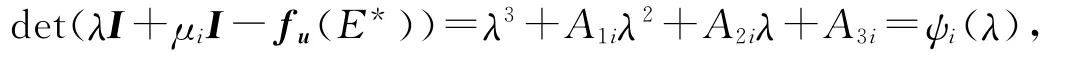
其中:
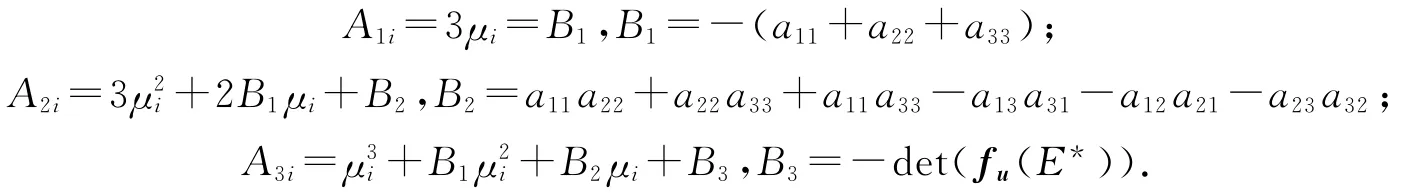
即
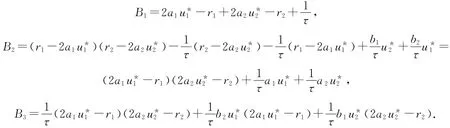
通過計算可得,當假設(H2)成立,并且a1,a2,b1,b2,r1,r2滿足
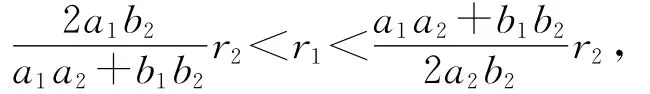
此時2a1u*1-r1>0,2a2u*2-r2>0,顯然B1,B2,B3>0,
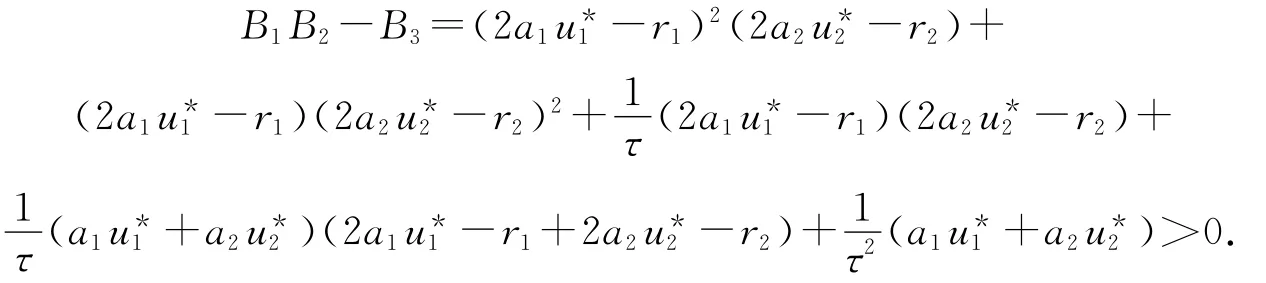
根據Routh-Hurwitz判別法,特征多項式的特征值具有負實部,所以E*是局部漸近穩定的.證畢.
3 正常值解的全局穩定性
為了研究E*穩定性,我們需要引入系統(1.4)的伴隨系統
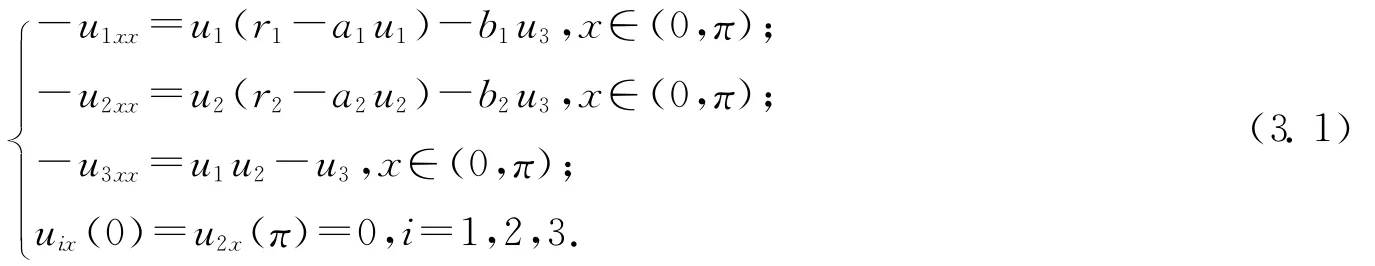
定義3.1[6]令

我們稱~c,^c是系統(3.1)的一對有序上下解.
對于^ci≤ui,vi≤~ci,i=1,2,3,可知存在常數

使得如下關系成立:
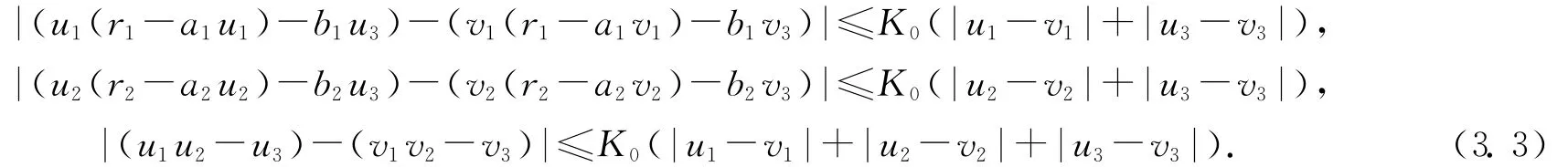
即系統(1.4)滿足Lipchitz條件,顯然系統(1.4)的右端函數連續,所以系統(1.4)存在位于[^c,~c]的解.構造序列
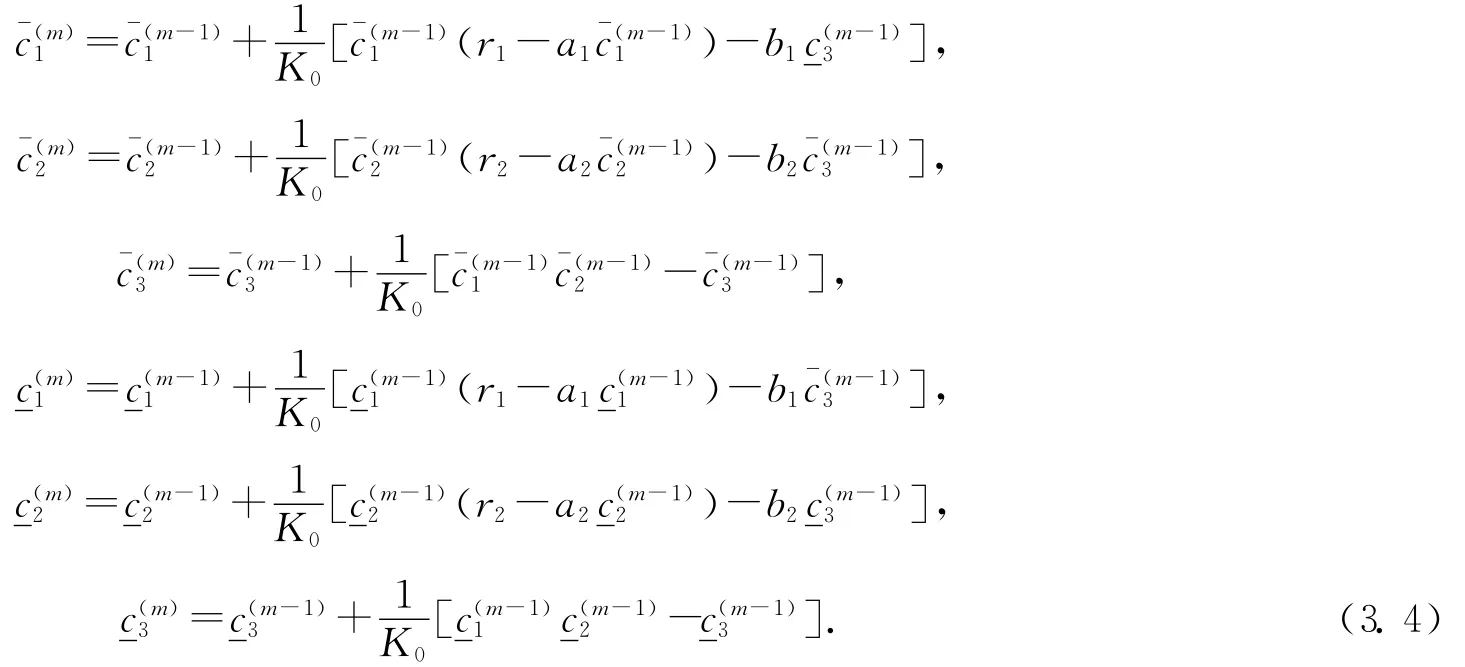
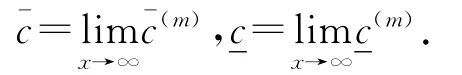
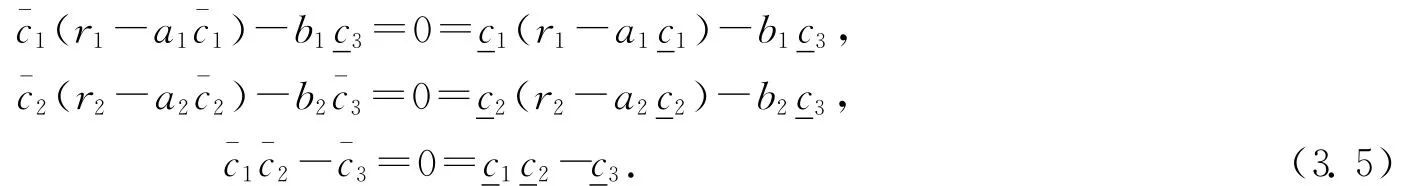
引理3.1[5]令,^c表示系統(3.1)的一對有序上下解,c表示(3.4)式中滿足(3.5)式的極限.則其對應的系統(1.4)的解u=(u1,u2,u3)在初始值i(x,θ)滿足^ci≤i(x,0)≤(i=1,2,3)的情況下滿足性質≤u(x,t)≤c,t→∞,x∈(0,π).進一步的,如果=c,則(或c)是系統(3.1)在,^c〉中的唯一解,且
定理3.1 令u=(u1,u2,u3)表示系統(1.4)在i(x,0)0,i=1,2,3條件下的解.假設(H2)成立,并且存在δ>0,使得
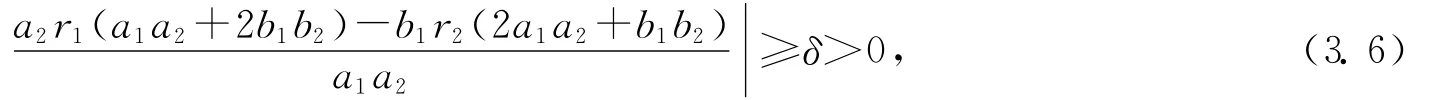
證明 u=(u1,u2,u3)表示系統(1.4)在i(x,0)0,i=1,2,3條件下的解,則有ui(x,y)>0,i=1,2,3,x∈[0,π],t>0.
首先,我們構造~c,^c使得~c≥^c≥0=(0,0,0),且(3.2)式成立.
令
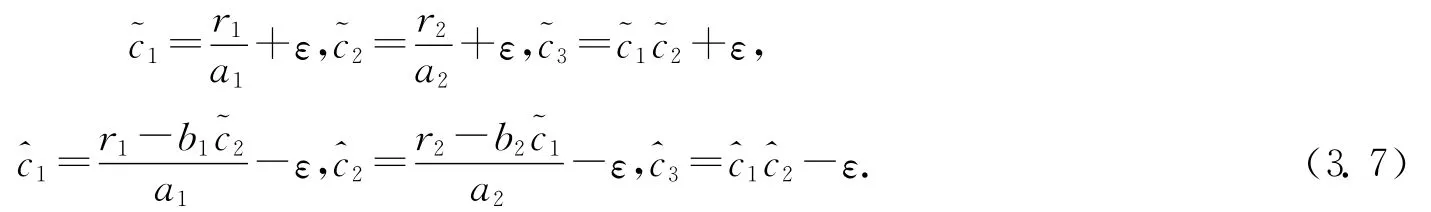
其中,ε>0且充分小,~c=(~c1,~c2,~c3),^c=(^c1,^c2,^c3).
其次,證明存在t*,使得當t≥t*時,^ci≤ui(x,t)≤~ci,(x,t)∈[0,π],i=1,2,3.由系統(1.4)知uit≤uixx+ui(ri-aiui),利用比較原理,
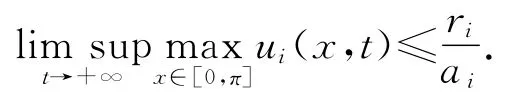
所以,對ε>0且充分小,?ti>0,使得當t≥ti時因此,有u3t≤u3xx+利用比較原理,
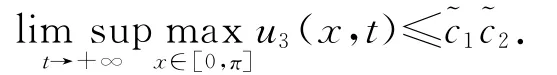
所以,對ε>0且充分小,?t3>max{t1,t2},使得當t≥t3時,u3(x,t)≤~c1~c2+ε=~c3.
由系統(1.4)及~c的值可知u1t≥u1xx+u1(r1-a1u1)-b1u3,(x,t)∈(t3,∞),又因為~c3≥~c1~c2≥u1~c2,所以只需證明u1t≥u1xx+u1(r1-a1u1)-b1u1~c2即可.利用比較原理,對ε>0且充分小,?t4>t3,使得當t≥t4時.同理,?t5>t3,使得當t≥t5時由系統(1.4)和利用比較原理,對ε>0且充分小,?t6>max{t4, t5},使得當t≥t6時,u3≥^c1^c2-ε.
再次,證明系統(1.4)的解u一致收斂于E*.
不失一般性,假設^ci≤i(x,t)≤~ci,i=1,2,3.由引理3.1可知存在使得系統(1.4)的唯一解u滿足0<^ci≤ci≤ui≤≤,i=1,2,3,t→∞.因此,(3.5)式變為
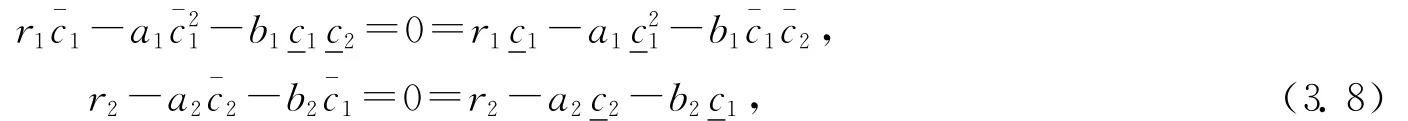
于是,
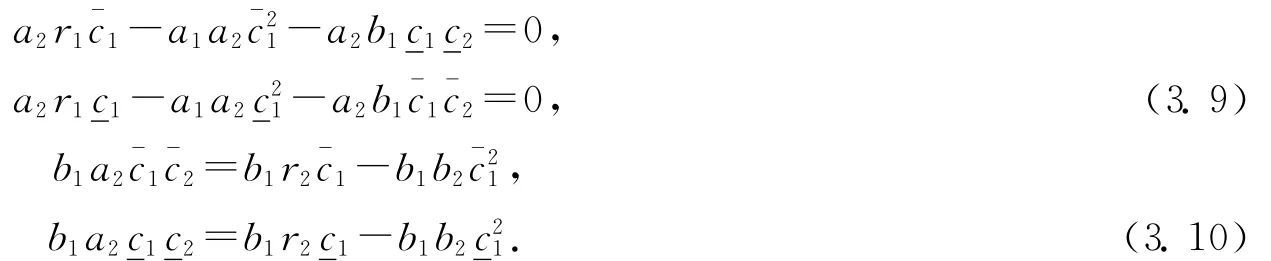
由(3.9)和(3.10)式,有
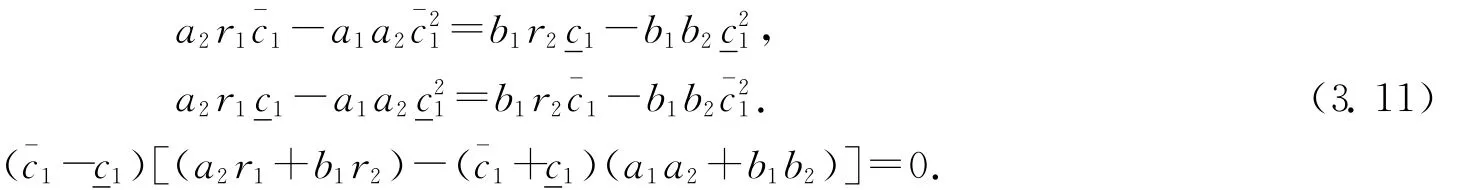
利用(3.6)式,對ε>0且充分小,有
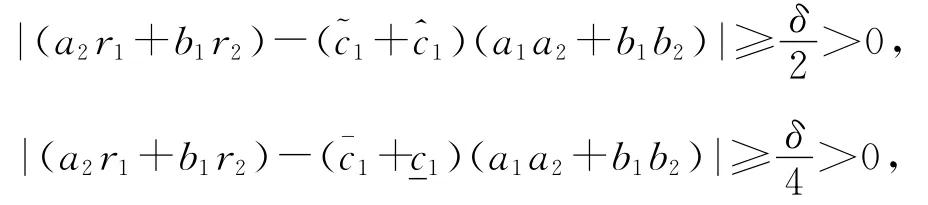
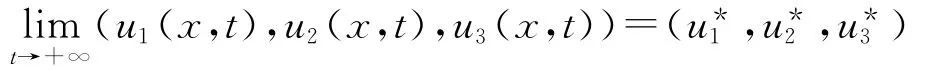
對x∈[0,π]一致成立.證畢.
[1] GOURLEY S A,RUAN S G.Convergence and travelling fronts in functional differential equations with nonlocal terms:a competition model[J].SIAM J Math Anal,2003,35(3):806-822.
[2] GOURLEY S A,SO J W H.Dynamics of a food-limited population model incorporating nonlocal delays on a finite domain[J].J Math Biol,2002,44:49-78.
[3] OMARI J AL,GOURLEY S.Monotone travelling fronts in an age-structured reaction-diffusion model of a single species[J].J Math Biol,2002,45:294-312.
[4] WANG Z C,LI W T,RUAN S G.Travelling wave fronts in reaction-diffusion systems with spatio-temporal delays[J].J Differential Equations,2006,222:185-232.
[5] 李玉環,周軍,穆春來.對帶有非局部時滯和擴散的捕食者-食餌系統的穩定性分析[J].數學物理學報,2012,32A(3):475-488.
[6] 葉其孝,李正元,王明新,等.反應擴散方程引論[M].第二版.北京:科學出版社,2011:76-134.
[7] 高芳,王文爽,王靜.帶有食餌避難的Leslie-Gower捕食者-食餌擴散系統的穩定性及最優稅收[J].東北師大學報:自然科學版,2014,46(1):1-8.
Stability analysis for a competitive system with nonlocal delayed and reaction-diffusion
SUN Ya-nan,MENG Lin,WANG Jing
(School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China)
In this paper,we study a competitive system with nonlocal delayed and reaction-diffusion in the condition of homogeneous Neumann boundary conditions.By using the linearization method and the method of upper and lower solutions,we conclude the local and global stability of the constant equilibrium.
competitive system;reaction-diffusion;equilibrium point;nonlocal delayed
O 175.14 [學科代碼] 110·34
A
(責任編輯:陶 理)
1000-1832(2015)03-0019-07
10.16163/j.cnki.22-1123/n.2015.03.005
2014-01-17
國家自然科學基金資助項目(11271065).
孫亞男(1989—),女,碩士;王靜(1972—),女,博士,副教授,主要從事微分方程和生態數學研究.

