廣東省能源需求預(yù)測(cè)模型構(gòu)建及實(shí)證分析*
葉藝勇
(五邑大學(xué) 經(jīng)濟(jì)管理學(xué)院 廣東 江門 529020)
1 引 言
隨著社會(huì)經(jīng)濟(jì)的快速發(fā)展,各行業(yè)對(duì)能源的需求大幅度增加.據(jù)統(tǒng)計(jì),廣東省2000年的能源消耗量是7 983萬噸標(biāo)準(zhǔn)煤,2013年的能源消耗量上升到25 645萬噸標(biāo)準(zhǔn)煤,是2000年消耗量的3.2倍,其中一次能源消費(fèi)90%依賴省外,二次能源消費(fèi)中的電力消費(fèi)有10%也是依賴省外,據(jù)估算,未來10年這個(gè)比例將達(dá)到30%左右.經(jīng)濟(jì)快速發(fā)展所帶來的巨大能源需求與供給不足之間的矛盾越來越嚴(yán)重,能源短缺已成為制約廣東省經(jīng)濟(jì)持續(xù)發(fā)展的關(guān)鍵問題,如果不采取有效的措施,將會(huì)延緩廣東省產(chǎn)業(yè)結(jié)構(gòu)的轉(zhuǎn)型升級(jí)優(yōu)化,乃至影響全省經(jīng)濟(jì)的穩(wěn)步增長.系統(tǒng)地分析廣東省能源需求的影響因素,準(zhǔn)確地預(yù)測(cè)廣東省未來能源需求的數(shù)量,進(jìn)而制定科學(xué)合理的能源發(fā)展戰(zhàn)略,確保廣東省經(jīng)濟(jì)可持續(xù)發(fā)展,具有非常重要的現(xiàn)實(shí)意義.
2 文獻(xiàn)綜述
能源系統(tǒng)是一個(gè)復(fù)雜的非線性系統(tǒng),其需求量受到眾多因素的影響.當(dāng)前很多學(xué)者已經(jīng)對(duì)能源需求問題進(jìn)行了深入的研究,使用的預(yù)測(cè)方法包括趨勢(shì)外推法、消費(fèi)彈性法、主要消耗部門預(yù)測(cè)法、回歸分析法預(yù)測(cè)等[1-3],取得了一定的效果.但在預(yù)測(cè)精度方面還存在一定的差距,一方面是由于能源系統(tǒng)本身的復(fù)雜性、非線性、非確定性的特征導(dǎo)致的,另一方面是因?yàn)轭A(yù)測(cè)方法本身還存在一些不足之處,不足以完全準(zhǔn)確反映預(yù)測(cè)目標(biāo)和指標(biāo)體系之間的數(shù)量關(guān)系.要解決上述問題,除了需要構(gòu)建科學(xué)的預(yù)測(cè)指標(biāo)體系,更關(guān)鍵的就是要尋找更加科學(xué)有效的預(yù)測(cè)方法.
鑒于此,部分學(xué)者開始研究能源系統(tǒng)的非線性和不確定性等系統(tǒng)特征,如自組織特征、分形特征、混沌特征和模糊性等,并在此基礎(chǔ)上引進(jìn)非線性方法對(duì)能源需求進(jìn)行預(yù)測(cè),如非線性/混沌時(shí)間序列方法、遺傳算法、灰色理論、人工神經(jīng)網(wǎng)絡(luò)方法等[4-8],這些方法可以彌補(bǔ)線性模型在預(yù)測(cè)復(fù)雜能源需求時(shí)的不足.其中具有代表性的方法是人工神經(jīng)網(wǎng)絡(luò),它是由大量神經(jīng)元通過極其豐富和完善的連接而構(gòu)成的自適應(yīng)、非線性動(dòng)態(tài)系統(tǒng),它從結(jié)構(gòu)、實(shí)現(xiàn)機(jī)理和功能上模擬生物神經(jīng)網(wǎng)絡(luò),通過并行分布式的處理方法,克服了傳統(tǒng)的基于邏輯符號(hào)的人工智能在處理直覺、非結(jié)構(gòu)化信息方面的缺陷,具有自適應(yīng)、自組織和實(shí)時(shí)學(xué)習(xí)的特點(diǎn)[9].它在解決非線性及高維模式識(shí)別問題中表現(xiàn)出許多特別的優(yōu)勢(shì),受到學(xué)者的青睞.當(dāng)前,已有眾多學(xué)者將神經(jīng)網(wǎng)絡(luò)及其擴(kuò)展模型應(yīng)用于時(shí)間序列預(yù)測(cè)方面,并取得了很好的效果[10-15].
通過對(duì)文獻(xiàn)的綜合分析發(fā)現(xiàn),神經(jīng)網(wǎng)絡(luò)及其相關(guān)的模型已經(jīng)被廣泛應(yīng)用到金融、工業(yè)、交通等領(lǐng)域,但是在能源需求預(yù)測(cè)領(lǐng)域的應(yīng)用較少.針對(duì)廣東省能源需求系統(tǒng)具有非線性和影響因素眾多等特征,建立了基于改進(jìn)的PSO-BP神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)模型,給出了方法的基本原理和具體實(shí)現(xiàn)步驟,然后通過對(duì)廣東省1985—2013年能源需求歷史數(shù)據(jù)的建模和仿真,驗(yàn)證了方法的有效性,最后對(duì)廣東省未來5年的能源需求進(jìn)行預(yù)測(cè),為能源管理者提供決策參考的依據(jù).
3 廣東省能源需求影響因素分析
能源需求受到多方面因素的影響,本文結(jié)合其他學(xué)者的研究成果[16-18],遵循可獲得性、可比性、實(shí)際性、綜合性的原則,從以下幾個(gè)方面對(duì)影響能源需求的因素進(jìn)行分析.
①經(jīng)濟(jì)增長.經(jīng)濟(jì)增長是影響能源需求的主要因素,隨著廣東省社會(huì)經(jīng)濟(jì)的快速發(fā)展和產(chǎn)業(yè)結(jié)構(gòu)的持續(xù)優(yōu)化,對(duì)能源的需求量將在很長一段時(shí)間內(nèi)保持較高的水平.衡量經(jīng)濟(jì)增長的指標(biāo)本文采用國內(nèi)生產(chǎn)總值(GDP).
②產(chǎn)業(yè)結(jié)構(gòu)調(diào)整.三大產(chǎn)業(yè)中,工業(yè)的發(fā)展對(duì)經(jīng)濟(jì)增長的貢獻(xiàn)最大,對(duì)能源的需求也最大,第一、第三產(chǎn)業(yè)對(duì)能源的需求相對(duì)較少.工業(yè)的快速發(fā)展所帶來的負(fù)面影響是顯而易見的.近年來,廣東省在產(chǎn)業(yè)結(jié)構(gòu)優(yōu)化和轉(zhuǎn)型升級(jí)方面出臺(tái)了一系列的政策措施,隨著我省產(chǎn)業(yè)結(jié)構(gòu)的調(diào)整,對(duì)能源需求數(shù)量的必將產(chǎn)生很大的影響.
③能源消費(fèi)結(jié)構(gòu).該項(xiàng)指標(biāo)反映了各種消費(fèi)能源在消費(fèi)總量中所占的比例關(guān)系,廣東省的能源消費(fèi)以煤為主,據(jù)統(tǒng)計(jì),超過50%的能源來自煤炭燃燒.煤炭為不可再生能源,利用率較低,容易污染環(huán)境,政府在大力推行開發(fā)可再生能源和清潔能源,改善能源消費(fèi)結(jié)構(gòu),降低能耗指數(shù).
④技術(shù)進(jìn)步.首先是通過先進(jìn)技術(shù)的應(yīng)用,改善生產(chǎn)工藝和流程,提高能源的利用率,節(jié)約能源消費(fèi);其次是將技術(shù)應(yīng)用于新能源開發(fā),從而改變能源消費(fèi)結(jié)構(gòu),進(jìn)而影響能源消費(fèi)總量.由于技術(shù)進(jìn)步難以量化,本文使用單位GDP的能耗來表示.
⑤人口和城市化.能源是人類生存和發(fā)展的物質(zhì)前提,人類的衣食住行與能源息息相關(guān),人口基數(shù)越大,對(duì)能源的需求量就越大,隨著工業(yè)化、城鎮(zhèn)化進(jìn)程的加快,人民生活水平穩(wěn)步提升,對(duì)能源需求的影響更加明顯.
⑥居民生活消費(fèi)水平.居民生活水平的提高,以及消費(fèi)觀念和消費(fèi)行為的變化,會(huì)直接導(dǎo)致產(chǎn)業(yè)結(jié)構(gòu)的變動(dòng),進(jìn)而影響能源消費(fèi)的數(shù)量,特別是增加對(duì)電力、液體和氣體燃料等優(yōu)質(zhì)能源的需求.
綜上所述,影響能源需求的主要因素有經(jīng)濟(jì)的增長(廣東省GDP)、產(chǎn)業(yè)結(jié)構(gòu)(工業(yè)在國民經(jīng)濟(jì)中的比重)、能源消費(fèi)結(jié)構(gòu)(煤炭的消費(fèi)比重)、技術(shù)進(jìn)步(單位GDP的能耗)、人口(廣東省人口數(shù)量)、城市化(全省城鎮(zhèn)人口所占的比重)、居民人均消費(fèi)水平,預(yù)測(cè)對(duì)象為廣東省每年的能源消費(fèi)數(shù)量.
4 PSO-BP能源需求預(yù)測(cè)模型構(gòu)建
4.1 BP神經(jīng)網(wǎng)絡(luò)模型
BP神經(jīng)網(wǎng)絡(luò)是一種多層前饋神經(jīng)網(wǎng)絡(luò),該網(wǎng)絡(luò)的主要特點(diǎn)是信號(hào)向前傳遞,誤差反向傳播.在前向傳遞中,輸入信號(hào)從輸入層經(jīng)過隱含層逐層處理,直至輸出層.每一層的神經(jīng)元狀態(tài)只影響下一層神經(jīng)元狀態(tài).如果輸出層得不到期望輸出,則轉(zhuǎn)入反向傳播,根據(jù)預(yù)測(cè)誤差調(diào)整網(wǎng)絡(luò)權(quán)值和閾值,從而使BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)輸出不斷逼近期望輸出[19].BP神經(jīng)網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)如圖1所示,BP算法如下.
1)各層權(quán)值及閾值的初始化.
2)輸入訓(xùn)練樣本,并利用訓(xùn)練樣本對(duì)網(wǎng)絡(luò)進(jìn)行訓(xùn)練,計(jì)算各層輸出.
3)求出并記錄各層的反向傳輸誤差.
4)按照權(quán)值以及閾值修正公式修正各層的權(quán)值和閾值.
5)按照新的權(quán)值重復(fù)2)和3).
6)若誤差符合預(yù)設(shè)要求或者達(dá)到最大學(xué)習(xí)次數(shù),則終止學(xué)習(xí).
7)使用訓(xùn)練好的模型對(duì)預(yù)測(cè)樣本進(jìn)行預(yù)測(cè).
4.2 標(biāo)準(zhǔn)粒子群優(yōu)化算法
粒子群優(yōu)化算法(Particle Swarm Optimization)源于對(duì)鳥類捕食行為的研究,鳥類捕食時(shí),每只鳥找到食物最簡單有效的方法就是搜尋當(dāng)前距離食物最近的鳥的周圍區(qū)域.PSO算法就是從這種生物種群行為特征中得到啟發(fā)并用于求解優(yōu)化問題的.算法中每個(gè)粒子代表問題的一個(gè)潛在解,每個(gè)粒子對(duì)應(yīng)一個(gè)由適應(yīng)度函數(shù)決定的適應(yīng)度值.粒子的速度決定了粒子移動(dòng)的方向和距離,速度隨自身及其他粒子的移動(dòng)經(jīng)驗(yàn)進(jìn)行動(dòng)態(tài)調(diào)整,從而實(shí)現(xiàn)個(gè)體在可解空間的尋優(yōu)[19].
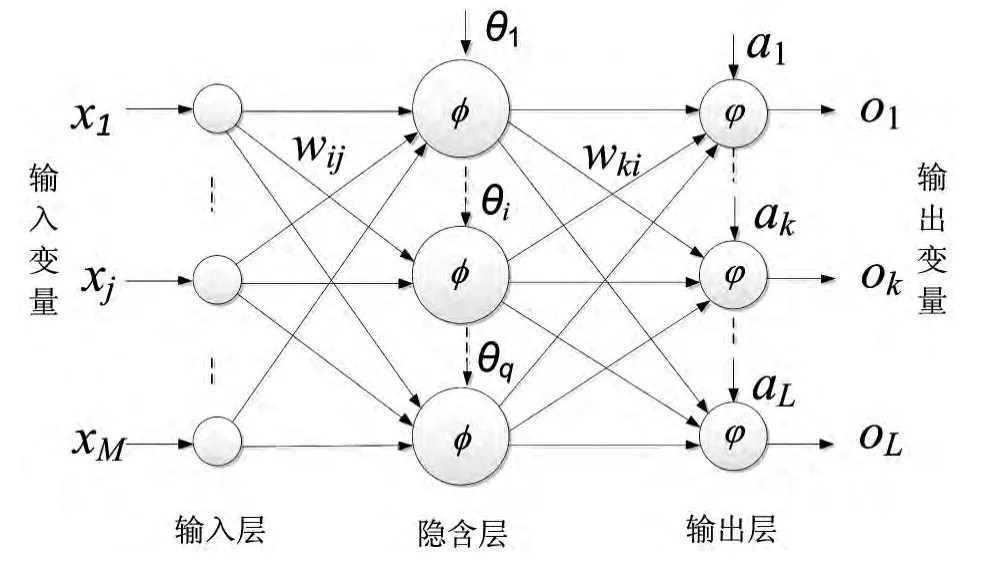
圖1 神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)圖
假設(shè)粒子群的種群規(guī)模為Z,搜索空間為Y維,第i個(gè)粒子的位置表示為
Xi={xi1,xi2,…,xiY},i=1,2,…,Z,第i個(gè)粒子的速度表示為Vi={vi1,vi2,…,viY,第i個(gè)粒子的個(gè)體極值表示為Pi={pi1,pi2,…,piY,當(dāng)前的全局極值表示為Pg={pg1,pg2,…,pgY.因此,粒子的速度與位置按下式更新:
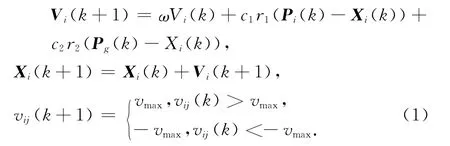
其中,ω為慣性權(quán)重,是平衡粒子的全局搜索能力和局部搜索能力的參數(shù);c1和c2為加速因子,是調(diào)整粒子自身經(jīng)驗(yàn)和群體經(jīng)驗(yàn)對(duì)粒子運(yùn)動(dòng)軌跡的影響的參數(shù);r1和r2是在[0,1]區(qū)間內(nèi)均勻分布的兩個(gè)隨機(jī)數(shù);vmax為粒子的最大速度,是用來限制粒子的速度的參數(shù),vij為第i個(gè)粒子在第j維的速度.
4.3 改進(jìn)的粒子群優(yōu)化算法
標(biāo)準(zhǔn)的粒子群算法雖然具有收斂速度快、通用性強(qiáng)等優(yōu)點(diǎn),但由于算法實(shí)現(xiàn)過程僅利用了個(gè)體最優(yōu)和全局最優(yōu)的信息,因此導(dǎo)致種群的多樣性消失過快,出現(xiàn)早熟收斂、后期迭代效率不高、容易陷入局部最優(yōu)等缺點(diǎn),增加了尋找全局最優(yōu)解的難度.要解決上述問題,可以從以下兩方面進(jìn)行改進(jìn).
4.3.1 動(dòng)態(tài)調(diào)整慣性權(quán)重
慣性權(quán)重ω用來控制粒子之前的速度對(duì)當(dāng)前速度的影響,它將影響粒子的全局和局部搜索能力.較大的ω值有利于全局搜索,較小ω值有利于局部搜索,但在標(biāo)準(zhǔn)的PSO算法中,ω的值是固定的,在算法運(yùn)行過程中,根據(jù)實(shí)際情況給ω賦予動(dòng)態(tài)變化的值,使得算法能夠平衡全局和局部搜索能力,這樣可以以最少的迭代次數(shù)找到最優(yōu)解.經(jīng)驗(yàn)參數(shù)是將ω初始值設(shè)定為0.9,并使其隨迭代次數(shù)的增加線性遞減至0.3,以達(dá)到上述期望的優(yōu)化目的.通過線性轉(zhuǎn)換來完成上述參數(shù)值變化的過程.
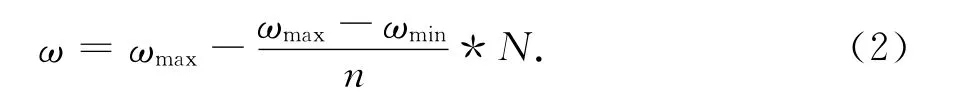
其中ωmax,ωmin分別是ω的最大值和最小值,n和N是當(dāng)前迭代次數(shù)和最大迭代次數(shù),在迭代開始時(shí)設(shè)ω=ωmax,ω在迭代過程中逐漸減小,直到ω=ωmin.
這樣設(shè)置使PSO算法能夠更好的控制探索與開發(fā)的關(guān)系,在開始優(yōu)化時(shí)搜索較大的解空間,找到合適的粒子,然后在后期逐漸收縮到較小的區(qū)域進(jìn)行更精細(xì)的搜索以加快收斂速度.
4.3.2 增加粒子的多樣性
在此借鑒遺傳算法中變異的思想,對(duì)部分符合條件的粒子以一定的概率重新初始化,目的是通過變異操作來保持種群的多樣性,拓展種群的搜索空間,使得粒子能夠跳出當(dāng)前局部最優(yōu)的位置,在更大的空間繼續(xù)搜索全局最優(yōu)值.引入線性動(dòng)態(tài)變異算子:

式中,F(xiàn)(n) 為當(dāng)前的變異概率;n為當(dāng)前的迭代次數(shù);N為最大的迭代次數(shù);Fmax,F(xiàn)min為最大的變異概率和最小的變異概率.
剛開始迭代時(shí),種群以一個(gè)極小的概率發(fā)生變異,至迭代后期,變異概率迅速擴(kuò)大,粒子可以迅速跳出當(dāng)前的搜索區(qū)域,在更大的區(qū)域內(nèi)尋找最優(yōu)解.
4.4 改進(jìn)的PSO-BP神經(jīng)網(wǎng)絡(luò)模型
BP神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)過程主要是權(quán)值和閾值的更新過程,采用的學(xué)習(xí)算法是以梯度下降為基礎(chǔ)的,但梯度下降法的訓(xùn)練效果過于依賴初始權(quán)值的選擇,且存在訓(xùn)練時(shí)間長、易陷入局部極小等問題.而粒子群算法可以避免梯度下降法中要求函數(shù)可微、對(duì)函數(shù)求導(dǎo)的過程,也避免了遺傳算法中的選擇、交叉等操作,具有收斂速度快、記憶性強(qiáng)和全局搜索能力較強(qiáng)等特點(diǎn)[20],可以將兩種算法結(jié)合起來,利用PSO算法中粒子的位置來對(duì)應(yīng)神經(jīng)網(wǎng)絡(luò)網(wǎng)絡(luò)中的連接權(quán)值和閾值,以神經(jīng)網(wǎng)絡(luò)的輸出誤差作為PSO算法的適應(yīng)函數(shù),通過PSO算法的優(yōu)化搜索來訓(xùn)練神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值,可以彌補(bǔ)BP網(wǎng)絡(luò)在學(xué)習(xí)能力和收斂速度上的不足,既充分發(fā)揮了神經(jīng)網(wǎng)絡(luò)的非線性映射能力,還可以縮短神經(jīng)網(wǎng)絡(luò)的訓(xùn)練時(shí)間,提高預(yù)測(cè)的精度.
PSO優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的主要步驟如下.
1)初始化.根據(jù)BP神經(jīng)網(wǎng)絡(luò)的輸入樣本,建立BP神經(jīng)網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu),輸入層節(jié)點(diǎn)數(shù),隱含層節(jié)點(diǎn)數(shù),輸出層節(jié)點(diǎn)數(shù);初始化粒子的位置和速度,以及粒子數(shù)、最大迭代次數(shù)、慣性權(quán)重、學(xué)習(xí)因子等參數(shù).
2)通過網(wǎng)絡(luò)訓(xùn)練,計(jì)算粒子的適應(yīng)度值,得到粒子的個(gè)體最優(yōu)值與全局最優(yōu)值.將粒子適應(yīng)度值與個(gè)體最優(yōu)值和全局最優(yōu)值相比較,記錄當(dāng)前粒子所經(jīng)歷的最好位置.
3)考察每一個(gè)粒子的適應(yīng)度值.若該值優(yōu)于個(gè)體最優(yōu),則將當(dāng)前值置為個(gè)體最優(yōu),并更新該粒子的個(gè)體最優(yōu);若粒子中的個(gè)體最優(yōu)優(yōu)于當(dāng)前的全局最優(yōu),則將個(gè)體最優(yōu)置為全局最優(yōu),并更新全局最優(yōu)值.
4)將經(jīng)過PSO優(yōu)化的權(quán)值和閾值作為BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值代入BP網(wǎng)絡(luò),訓(xùn)練至滿足網(wǎng)絡(luò)的性能指標(biāo),即均方誤差小于預(yù)先設(shè)定的誤差要求或達(dá)到最大迭代次數(shù)時(shí),停止迭代,輸出結(jié)果,否則轉(zhuǎn)到2,繼續(xù)迭代直至算法收斂.
5)由訓(xùn)練和測(cè)試樣本完成神經(jīng)網(wǎng)絡(luò)的訓(xùn)練和測(cè)試,輸出預(yù)測(cè)值.如圖2所示.
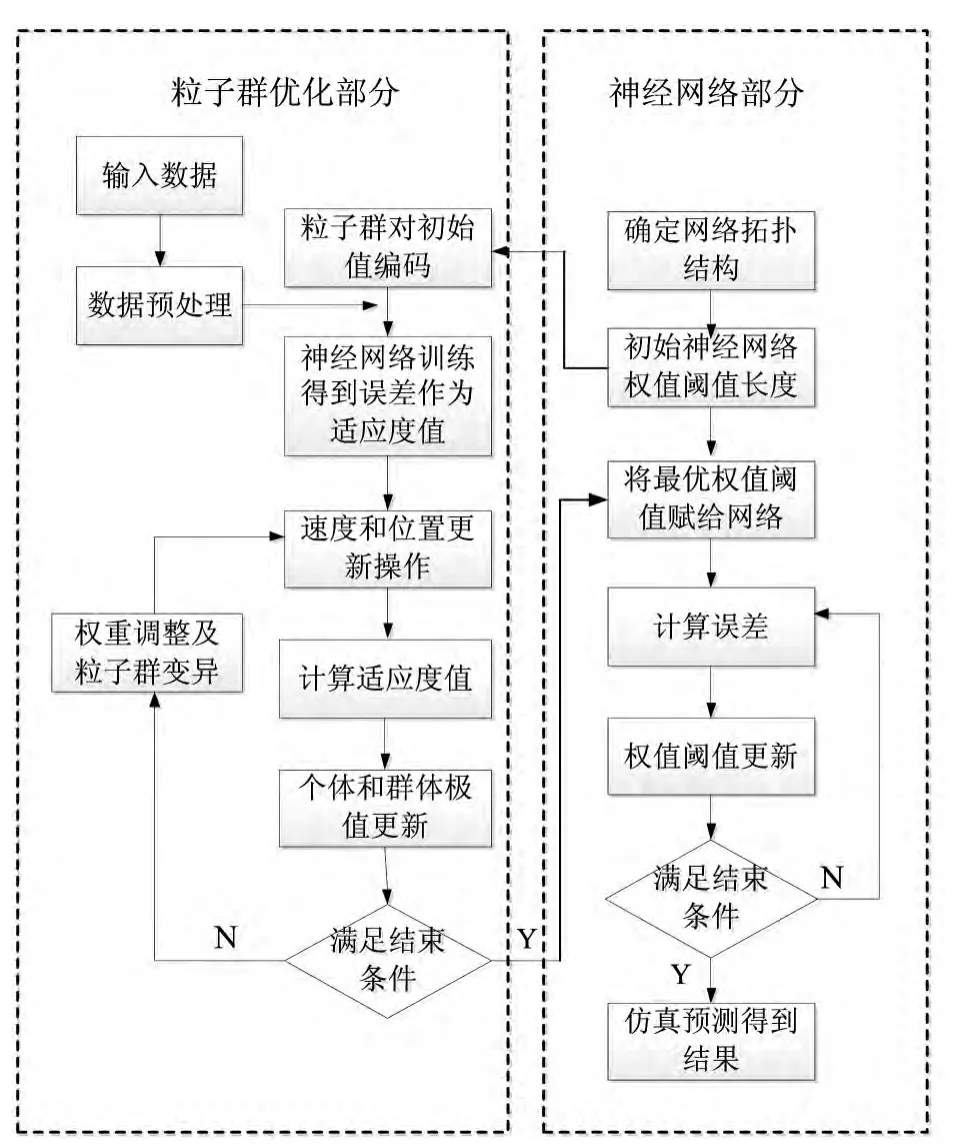
圖2 PSO優(yōu)化BP流程圖
5 實(shí)證分析
5.1 數(shù)據(jù)來源
數(shù)據(jù)來源見表1.
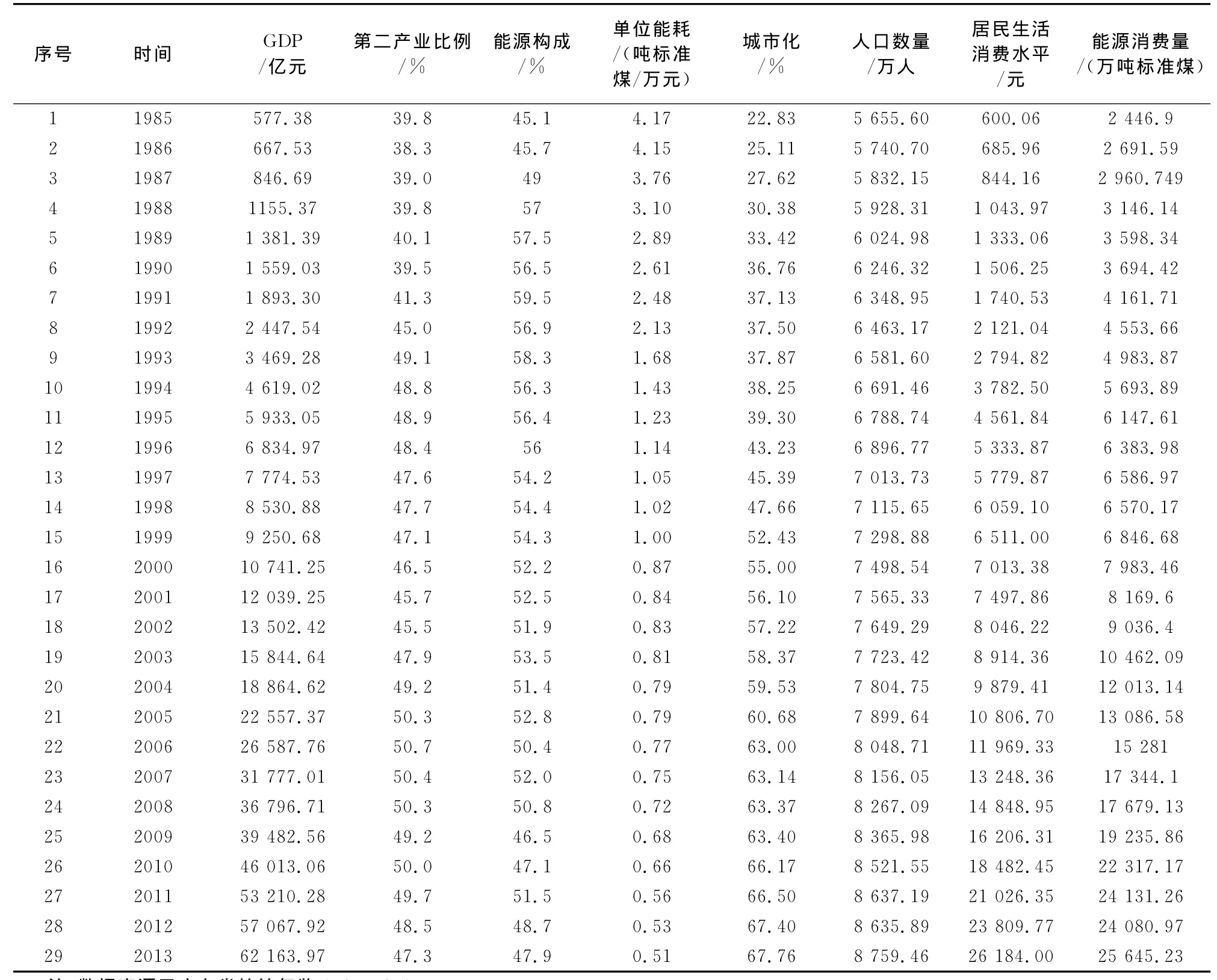
表1 各指標(biāo)統(tǒng)計(jì)數(shù)據(jù)
5.2 數(shù)據(jù)預(yù)處理
為了消除各指標(biāo)不同量綱的影響,需要對(duì)數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理,以解決指標(biāo)之間的可比性.本文使用離差標(biāo)準(zhǔn)化的方法,對(duì)原始數(shù)據(jù)進(jìn)行線性變換,使變換后的值映射到[0,1]之間,并保持原本的數(shù)量關(guān)系,變換公式如(4)式所示.
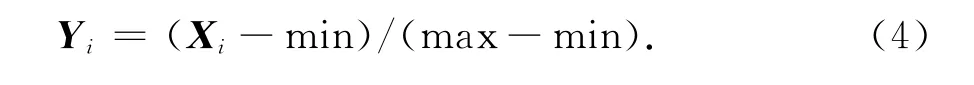
其中,Yi是樣本i歸一化的值,Xi是樣本i的值,min為樣本最小值,max為樣本最大值.但這個(gè)方法有個(gè)缺點(diǎn),當(dāng)有新的樣本數(shù)據(jù)加入時(shí),數(shù)據(jù)的最大值和最小值可能會(huì)發(fā)生變化,需要重新計(jì)算Yi值.
在預(yù)測(cè)或者評(píng)價(jià)完成后,再使用反歸一化的方法對(duì)數(shù)據(jù)進(jìn)行還原處理,得出其真實(shí)值,具體的數(shù)據(jù)處理過程可以直接調(diào)用Matlab工具箱里的Mapminmax函數(shù)來完成.
5.3 數(shù)據(jù)降維
就神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)而言,預(yù)測(cè)指標(biāo)體系越龐大,指標(biāo)數(shù)量越多,模型就越復(fù)雜,預(yù)測(cè)結(jié)果的不確定性就越大,相應(yīng)地,模型的泛化能力會(huì)降低,同時(shí)也會(huì)增加運(yùn)算的時(shí)間.因此有必要對(duì)前面確定的影響能源需求的指標(biāo)進(jìn)行定量化的分析,在盡量減少信息丟失的前提下減少指標(biāo)的個(gè)數(shù),即完成樣本指標(biāo)的降維.
主成分分析法就是通過線性變換的方法,把原始變量組合成少數(shù)幾個(gè)具有代表意義的指標(biāo),使得變換后的指標(biāo)能夠更加集中地反映研究對(duì)象特征的一種統(tǒng)計(jì)方法[21].對(duì)樣本的原始數(shù)據(jù)進(jìn)行主成分分析,得到各個(gè)主成分的特征值和方差貢獻(xiàn)率,如表2所示.
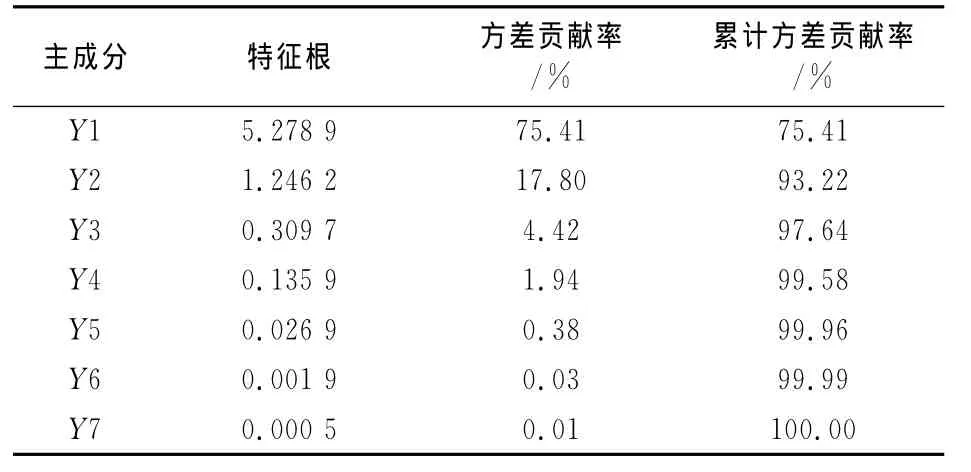
表2 主成分特征值和方差貢獻(xiàn)率
從表2的數(shù)據(jù)可知,當(dāng)抽取的主成分為Y1,Y2時(shí),主成分的累計(jì)方差貢獻(xiàn)率已達(dá)到93.22%,基本覆蓋了原來7個(gè)指標(biāo)所包含的信息.因此可以把Y1,Y2這2個(gè)主成分的數(shù)據(jù)作為模型的輸入,這樣就大幅度減少了神經(jīng)網(wǎng)絡(luò)的輸入節(jié)點(diǎn)數(shù),降低了模型的復(fù)雜程度,同時(shí)也有利于前期樣本數(shù)據(jù)的獲取.
根據(jù)主成分分析法得出前2個(gè)主成分的系數(shù)如表3所示.

表3 Y1和Y2的主成分系數(shù)
因此得出Y1、Y2與原輸入指標(biāo)的關(guān)系為:
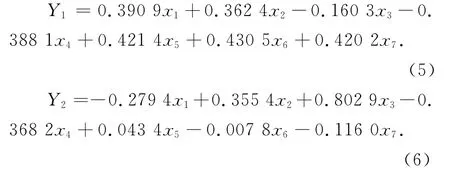
從表達(dá)式(5)可以看出,第一主成分Y1與x1、x2、x5、x6、x7均保持了較強(qiáng)的正相關(guān),而與x3,x4呈現(xiàn)出負(fù)相關(guān),這個(gè)數(shù)量關(guān)系說明了第一主成分基本反映了上述指標(biāo)的信息.由于x1、x2、x5、x6、x7是從不同的方面反映了社會(huì)經(jīng)濟(jì)發(fā)展的水平,而x3和x4反映了能源消費(fèi)的狀況,因此,第一主成分Y1是綜合反映了經(jīng)濟(jì)發(fā)展?fàn)顩r和能源需求之間的密切關(guān)系.
從表達(dá)式(6)可以看出,第二主成分Y2與x1、x2、x3、x4相關(guān)性較強(qiáng),其中與x3(能源結(jié)構(gòu))是高度相關(guān)的,說明第二主成分基本反映了這個(gè)指標(biāo)的信息.
5.4 模型參數(shù)設(shè)置
神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)一般由樣本的輸入和輸出指標(biāo)數(shù)量確定,由于使用PCA做數(shù)據(jù)降維后,樣本數(shù)據(jù)的維數(shù)為2,輸出數(shù)據(jù)維數(shù)為1,所以確定模型的輸入節(jié)點(diǎn)數(shù)為2,輸出節(jié)點(diǎn)數(shù)為1.本文選用的是三層的BP神經(jīng)網(wǎng)絡(luò)模型,關(guān)于隱含層數(shù)目的確定,目前沒有一個(gè)通用的方法,只能根據(jù)經(jīng)驗(yàn)或者多次試驗(yàn)來決定.由于隱含層的數(shù)量會(huì)影響到模型的學(xué)習(xí)時(shí)間、擬合效果以及泛化能力,因此必須確定一個(gè)最佳的隱含層單元數(shù),根據(jù)相關(guān)學(xué)者的研究結(jié)論,隱含層的數(shù)量與問題的要求、輸入、輸出指標(biāo)的個(gè)數(shù)都有關(guān)系,且其數(shù)量關(guān)系符合以下的計(jì)算公式[21]:

其中R為隱含層單元數(shù),S1、S2分別為輸入層和輸出層的數(shù)量,a為[1,10]之間的常數(shù).經(jīng)過循環(huán)比較算法,得出R的值為4時(shí),模型具有較好的學(xué)習(xí)效果和泛化能力,因此本文確定神經(jīng)網(wǎng)絡(luò)模型的結(jié)構(gòu)為2-4-1,隱層使用sigmoid函數(shù),輸出層使用pureline函數(shù),神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)效率取0.1,訓(xùn)練次數(shù)為150,輸出目標(biāo)值為0.001.粒子群規(guī)模為50,迭代次數(shù)為100,學(xué)習(xí)因子c1=1.7,c2=1.5,慣性權(quán)重ωmax=0.9,ωmin=0.3,粒子速度最大值為5,最小值為-5.
5.5 模型訓(xùn)練
本文選取前24個(gè)樣本數(shù)據(jù)作為訓(xùn)練數(shù)據(jù),用于確定模型的相關(guān)參數(shù),剩余5個(gè)樣本作為測(cè)試數(shù)據(jù),用于檢驗(yàn)?zāi)P偷男Ч?/p>
將訓(xùn)練數(shù)據(jù)代入模型進(jìn)行計(jì)算,得到的適應(yīng)度曲線變化如圖3所示,訓(xùn)練值與實(shí)際值比較如圖4所示,可以看出PSO-BP模型對(duì)歷史數(shù)據(jù)的學(xué)習(xí)情況非常理想,大部分樣本的訓(xùn)練值與實(shí)際值基本吻合,個(gè)別樣本有一定的偏差,但在合理的誤差范圍之內(nèi),說明該模型的構(gòu)建是行之有效的.
5.6 模型測(cè)試
將訓(xùn)練后的模型對(duì)5個(gè)預(yù)測(cè)樣本數(shù)據(jù)進(jìn)行預(yù)測(cè),并把預(yù)測(cè)值與實(shí)際值進(jìn)行比較,結(jié)果如表4所示,預(yù)測(cè)結(jié)果如圖5所示,樣本誤差如圖6所示.可以看到,2009-2013年的預(yù)測(cè)準(zhǔn)確度非常高,平均誤差為2.3%,以2009年為例,預(yù)測(cè)偏差為2.87%,換算成實(shí)際的偏差數(shù)量就是552.95萬噸標(biāo)準(zhǔn)煤,準(zhǔn)確的預(yù)測(cè)結(jié)果將為能源規(guī)劃與實(shí)施提供有力的依據(jù).
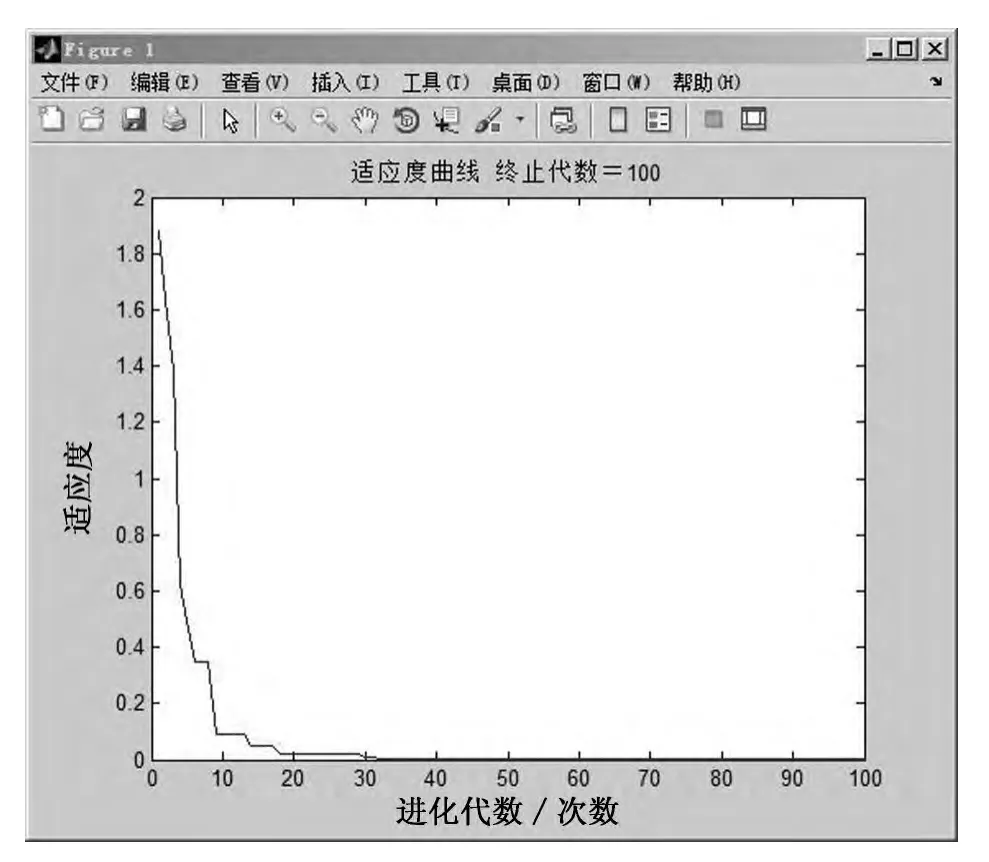
圖3 適應(yīng)度變化曲線圖
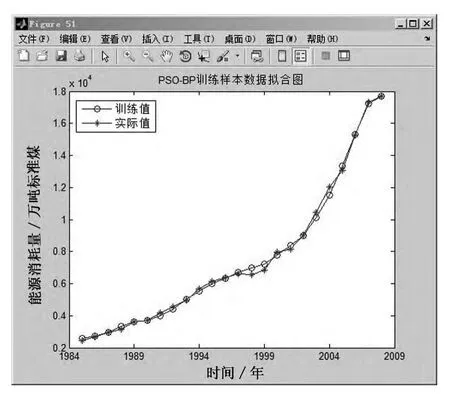
圖4 訓(xùn)練值與實(shí)際值比較圖

表4 預(yù)測(cè)值與實(shí)際值比較 萬噸標(biāo)準(zhǔn)煤
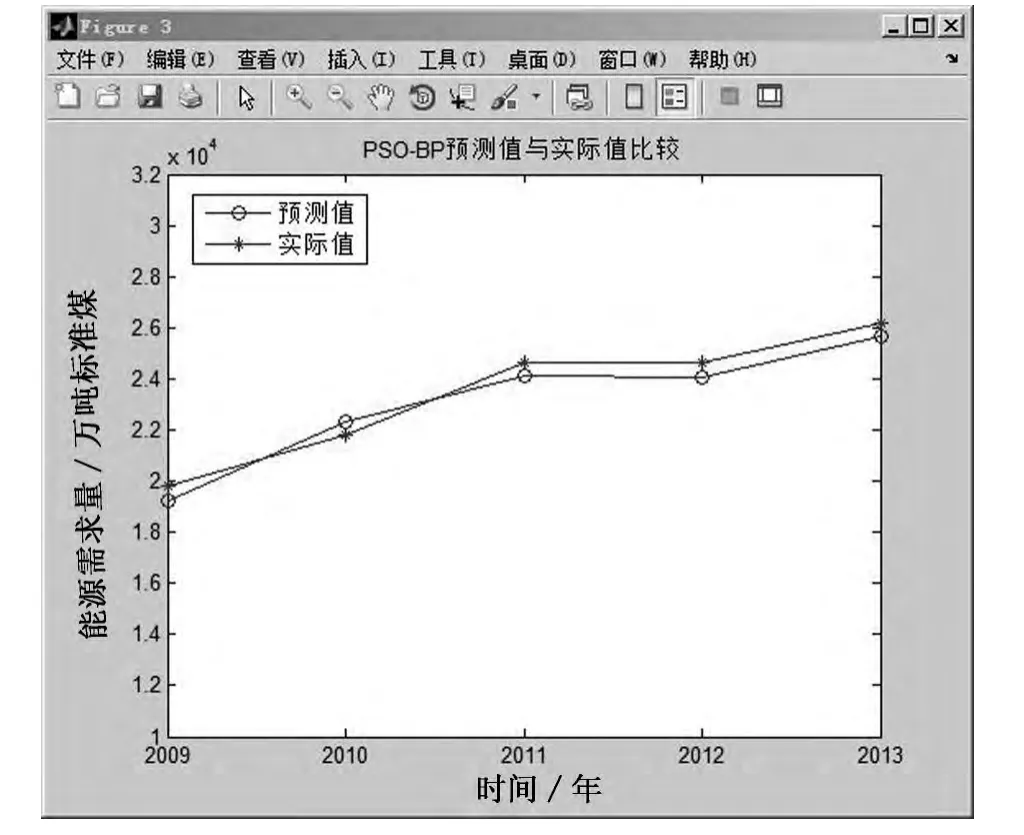
圖5 預(yù)測(cè)值與實(shí)際值比較
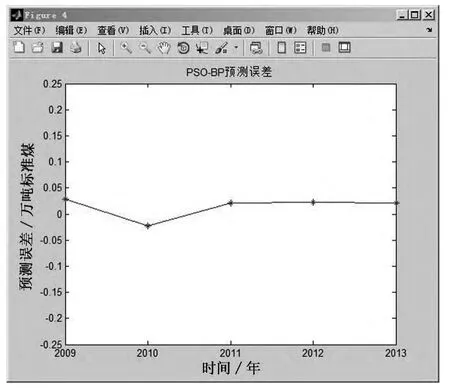
圖6 樣本誤差圖
圖7為神經(jīng)網(wǎng)絡(luò)在訓(xùn)練、驗(yàn)證及測(cè)試過程中,均方誤差的變化趨勢(shì),可以看到,當(dāng)訓(xùn)練次數(shù)達(dá)到一定的程度,均方誤差將會(huì)小于1×10-3,完全符合模型的預(yù)設(shè)要求.圖8為模型對(duì)樣本數(shù)據(jù)的擬合程度,根據(jù)R的取值,結(jié)合圖7的均方誤差,可知模型的學(xué)習(xí)能力及預(yù)測(cè)能力是非常強(qiáng)的,準(zhǔn)確度非常高.
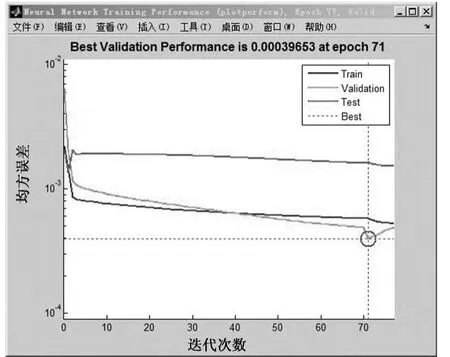
圖7 均方誤差的變化狀態(tài)
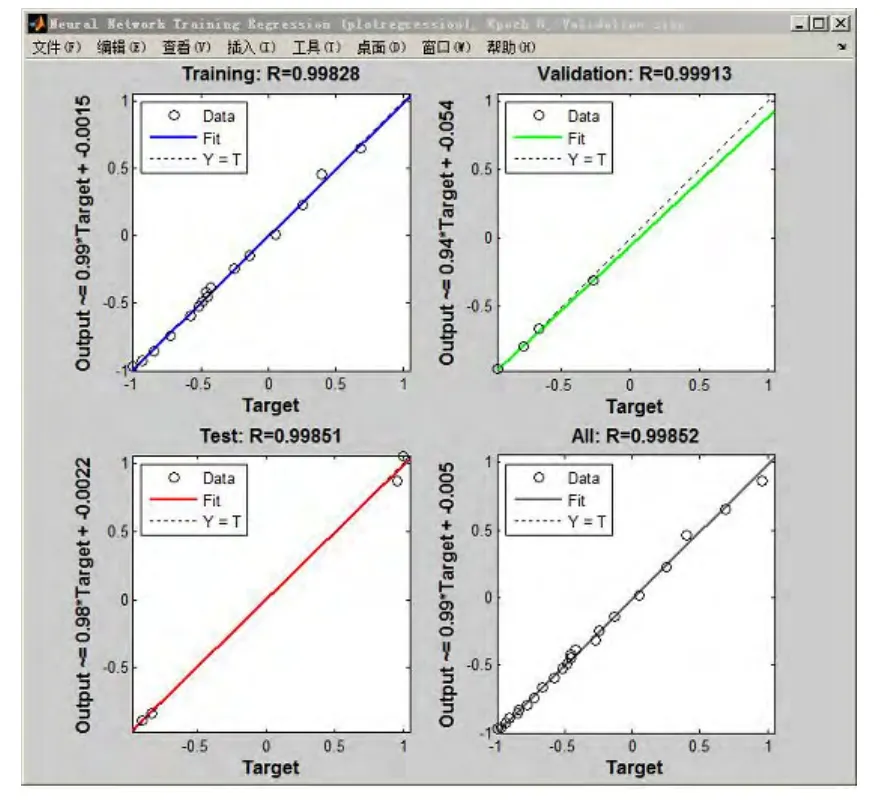
圖8 訓(xùn)練、驗(yàn)證及測(cè)試的性能狀態(tài)
5.7 不同方法預(yù)測(cè)結(jié)果比較
為了體現(xiàn)PSO-BP神經(jīng)網(wǎng)絡(luò)模型的優(yōu)勢(shì),本文同時(shí)使用未經(jīng)優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)對(duì)數(shù)據(jù)進(jìn)行訓(xùn)練和預(yù)測(cè),并將兩種預(yù)測(cè)結(jié)果進(jìn)行比較,具體數(shù)據(jù)見表5所示,比較效果如圖9和圖10所示.

表5 預(yù)測(cè)值與實(shí)際值比較(單位:萬噸標(biāo)準(zhǔn)煤)
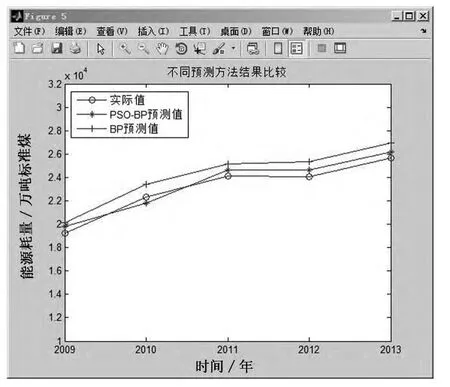
圖9 預(yù)測(cè)結(jié)果比較
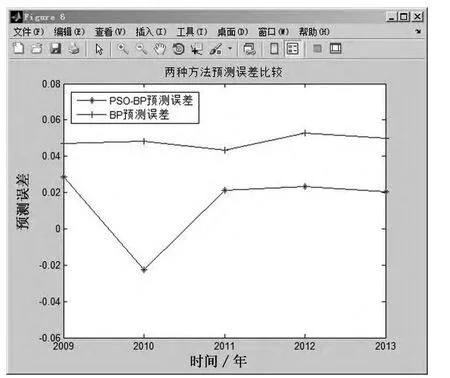
圖10 預(yù)測(cè)誤差比較A
由表5可知,PSO-BP模型的預(yù)測(cè)平均誤差為2.3%,BP模型的平均預(yù)測(cè)誤差為4.8%,說明經(jīng)過粒子群算法優(yōu)化神經(jīng)網(wǎng)絡(luò)參數(shù)后,不僅使得模型的收斂速度加快,運(yùn)算時(shí)間減少,同時(shí)在預(yù)測(cè)精度方面也有了很大的提升.
5.8 未來5年能源需求預(yù)測(cè)
根據(jù)上述預(yù)測(cè)模型和流程,對(duì)廣東省未來5年的能源需求進(jìn)行預(yù)測(cè),這里假設(shè)未來5年各項(xiàng)樣本指標(biāo)均保持當(dāng)前的增長速度,得出的結(jié)果見表6.

表6 2014~2018年能源需求量(單位:萬噸標(biāo)準(zhǔn)煤)
從表6可知,未來5年,廣東省的能源需求將持續(xù)增長,平均保持5.7%的增長率,并且增長的速度逐步加快,2018年的需求量將達(dá)到33 842.34萬噸標(biāo)準(zhǔn)煤.因此,如何針對(duì)快速增長的能源需求,采取有效的措施來解決供需不平衡的矛盾,將是決策者需要考慮的問題.根據(jù)廣東省發(fā)改委2013年底公布的《廣東省能源發(fā)展十二五規(guī)劃》,在保證全省能源供應(yīng)能力的前提下,將進(jìn)一步加快能源消費(fèi)結(jié)構(gòu)的調(diào)整,構(gòu)建與科學(xué)發(fā)展要求相適應(yīng)的安全、穩(wěn)定、經(jīng)濟(jì)、清潔的現(xiàn)代能源供應(yīng)保障體系,具體措施是進(jìn)一步優(yōu)化能源結(jié)構(gòu)和布局,提升能源利用效率,逐步降低單位GDP能耗,并且爭取在新能源的利用開發(fā)方面取得突破性進(jìn)展,從而為全省經(jīng)濟(jì)社會(huì)發(fā)展提供強(qiáng)有力的能源保障.
6 結(jié) 論
對(duì)廣東省的能源需求問題進(jìn)行了深入的研究,在結(jié)合定性和定量分析的基礎(chǔ)上,確定了影響能源需求的主要因素,構(gòu)建了PSO-BP神經(jīng)網(wǎng)絡(luò)的能源需求預(yù)測(cè)模型,并對(duì)廣東省2014-2018年的能源需求進(jìn)行了預(yù)測(cè).理論分析和實(shí)證研究表明,該方法能夠很好的反映廣東省能源需求的特征,預(yù)測(cè)結(jié)果較為準(zhǔn)確合理.但就本文所考慮的預(yù)測(cè)指標(biāo)體系而言,以定量的指標(biāo)為主,如何在模型中把政策法規(guī)、環(huán)境保護(hù)等難以定量的影響因素包含進(jìn)來,構(gòu)建更為完善的預(yù)測(cè)指標(biāo)體系,以及當(dāng)樣本數(shù)量較少的時(shí)候,如何保證模型的學(xué)習(xí)能力和泛化能力,這些問題需要繼續(xù)完善解決.
[1]林伯強(qiáng).中國能源需求的經(jīng)濟(jì)計(jì)量分析[J].統(tǒng)計(jì)研究,2001(10):34-39.
[2]韓君.中國能源需求的建模與實(shí)證分析[D].蘭州商學(xué)院,2007.
[3]魏一鳴等.中國能源需求報(bào)告(2006):戰(zhàn)略與政策研究[M].北京:科學(xué)出版社,2006.
[4]A S WEIGEND.Time series analysis and predicationusing gated experts with application to energy demandforecast[J].Applied Articial Intelligence,1996(6):583-624.
[5]V GEVORGIAN ,M KAISER .Fuel distribution andconsumption simulation in the republic of Armenia[J].Simulation,1998(3):154-167.
[6]張玉春,郭寧,任劍翔.基于組合模型的甘肅省能源需求預(yù)測(cè)研究[J].生產(chǎn)力研究,2012(11):31-34.
[7]馮亞娟,劉曉愷,張波.基于QGA-LSSVM的能源需求預(yù)測(cè)[J].科技與經(jīng)濟(jì),2014(3):56-61.
[8]蘆森.基于組合模型的中國能源需求預(yù)測(cè)[D].成都:成都理工大學(xué),2010.
[9]李琳娜.基于核主成分分析(KPCA)和神經(jīng)網(wǎng)絡(luò)的單目紅外圖像深度估計(jì)[D].上海:東華大學(xué),2013.
[10]張均東,劉澄,孫彬.基于人工神經(jīng)網(wǎng)絡(luò)算法的黃金價(jià)格預(yù)測(cè)問題研究[J].經(jīng)濟(jì)問題,2010(1):45-48.
[11]熊志斌.ARIMA融合神經(jīng)網(wǎng)絡(luò)的人民幣匯率預(yù)測(cè)模型研究[J].?dāng)?shù)量經(jīng)濟(jì)技術(shù)經(jīng)濟(jì)研究,2011(6):75-81.
[12]龍文,梁昔明,龍祖強(qiáng),等.基于混合進(jìn)化算法的RBF神經(jīng)網(wǎng)絡(luò)時(shí)間序列預(yù)測(cè)[J].控制與決策,2012(8):20-25.
[13]王慶榮,張秋余.基于隨機(jī)灰色蟻群神經(jīng)網(wǎng)絡(luò)的近期公交客流預(yù)測(cè)[J].計(jì)算機(jī)應(yīng)用研究,2012(6):32-37.
[14]張大斌,李紅燕,劉肖,等.非線性時(shí)間序列的小波-模糊神經(jīng)網(wǎng)絡(luò)集成預(yù)測(cè)方法[J].中國管理科學(xué),2013(2):81-86.
[15]高玉明,張仁津.基于遺傳算法和BP神經(jīng)網(wǎng)絡(luò)的房價(jià)預(yù)測(cè)分析[J].計(jì)算機(jī)工程,2014(4):187-191.
[16]伍秀君.廣東省能源需求預(yù)測(cè)分析及能源發(fā)展對(duì)策研究[D].廣州:暨南大學(xué),2007.
[17]薛黎明.中國能源需求影響因素分析[D].徐州:中國礦業(yè)大學(xué),2010.
[18]秦國真.云南能源需求影響因素分析及預(yù)測(cè)[D].昆明:云南財(cái)經(jīng)大學(xué),2012.
[19]來建波.基于神經(jīng)網(wǎng)絡(luò)的路段行程時(shí)間預(yù)測(cè)研究[D].昆明:云南大學(xué),2011.
[20]潘昊;侯清蘭.基于粒子群優(yōu)化算法的BP網(wǎng)絡(luò)學(xué)習(xí)研究[J].計(jì)算機(jī)工程與應(yīng)用,2006(6):65-69.
[21]郭陽.PSO-BP神經(jīng)網(wǎng)絡(luò)在商業(yè)銀行信用風(fēng)險(xiǎn)評(píng)估中的應(yīng)用研究[D].廈門:廈門大學(xué),2009.

