求積元法在金融工程計算領域應用初探

楊燕曦

摘要金融工程領域的大量實際問題最終都可歸結為對隨機微分方程（組）的求解.針對金融工程計算領域涉及到的靜態一維問題，首次將求積元方法應用于非自伴隨微分方程的求解.建立了相應的求積元方法計算單元.對典型問題進行計算，并與解析解、有限差分解、有限元解分別進行對比.結果表明，求積元法是一種簡單準確高效的數值方法，可進一步用于金融工程計算領域動態問題、二維問題的計算分析.

關鍵詞數理經濟；數值方法；求積元法

中圖分類號F830.91 文獻標識碼A

A Preliminary Study on the Application of QEM

in Financial Engineering Analysis

YANG Yanxi

（Party School of the Organ Directly Under the Hunan CPC Provincial Committee， Changsha， Hunan410079， China）

AbstractMany practical problems in modern finance can be cast into the framework of stochastic differential equations. The static 1D problem in financial engineering characterized by nonselfadjoint was examined in this paper by using the Quadrature Element Method （QEM） for the first time. The quadrature element for the problem mentioned above was established， and numerical results from QEM were compared with the analytic solution， FDM and FEM respectively. It is shown that high computational accuracy and efficiency are achieved using QEM， and this method can be further used in dynamic problem， 2D problem of financial engineering.

Key wordsMathematical Economics；Numerical Method；Quadrature Element Method

1引言

隨著科學技術的不斷發展，在現代金融工程領域愈來愈重視定量的數理分析，大量的實際問題，如動態最優定價、金融衍生產品的定價、投資風險的規避等，經過數理建模，最終都歸結為對隨機微分方程（組）的求解[1-3].這些微分方程（組）中很多都不易求得解析解，發展相應的數值解法具有重大意義.傳統的數值求解方法主要包括二叉樹方法，蒙特卡洛方法、有限差分法[4]，這些方法對計算機的計算能力要求較低，計算精度不高.近年來，國內外學者又將有限元法應用于金融工程計算領域[5]，提高了計算的精度和效率，但其收斂性和穩定性還有待進一步研究.當前，金融活動的風險及復雜性進一步加劇，數理建模得到的微分方程規模更大、復雜程度更高，有的還具有一定的非線性，迫切需要一種簡潔、準確、高效的數值計算方法.

求積元方法是一種結合了高效數值積分和微分求積法二者優勢的新的求解常（偏）微分方程（組）的

高階數值方法.該方法自2007年由清華大學鐘宏志教授提出以來，在工程結構分析領域中已得到較為廣泛地應用[6-9]，展現出其相比傳統有限元法的獨特優勢.

工程結構計算分析所涉及的微分方程（組）一般均具有線性自伴隨的特性，因而具有相應的變分形式.而對于金融工程計算分析中所涉及的微分方程（組）一般不具有自伴隨的特性，對于求積元方法的應用還是一個新的領域.

針對金融工程計算領域的靜態一維問題，將求積元方法應用于非自伴隨的微分方程的數值求解，建立相應的求積元單元.選取3個典型問題進行計算，與解析解、有限差分解和有限元解分別進行比較，驗證求積元方法的適應性、準確性和高效性.為該方法在金融工程計算領域動態問題（期權定價問題）、二維問題中的深入應用奠定基礎.

2一維邊值問題的求積元離散

一般地，金融工程中的靜態一維問題可用如下微分方程

u″（x）+a1（x）u′（x）+a2（x）u（x）+f（x）=0（1）

和相應的邊界條件表示，

α1u（xmin）+β1u′（xmin）=γ1，（2）

α2u（xmax）+β2u′（xmax）=γ2.（3）

式（1）中，ux為定義在區域xmin，xmax上的未知（待求）函數，u″x、u′x分別表示對x求二階、一階導數.a1x、a2x、fx為已知函數.式（2）、式（3）為邊界條件.

假設未知函數ux可以用近似函數x來表示，基于Galerkin加權殘值積分近似為零和求積元法求解思想，權函數選定為近似函數的變分δ，令式（1）殘值在加權積分意義下為零，即

∫xmaxxminδ″+a1′+a2+fdx=0.（4）

對式（4）中的二階導數進行分部積分

∫xmaxxminδ″+a1′+a2+fdx

=′δxmaxxmin-∫xmaxxmin′δ′dx

+∫xmaxxminδa1′+a2+fdxendprint

=∫xmaxxmin-′δ′+a1′δ+a2δ+fδdx

+b.t.=0.（5）

式（5）中，b.t.表示邊界條件.

將式（5）中積分進一步離散，根據求積元求解基本步驟，首先將待求解物理域坐標系通過式（6）轉換到標準域，如圖1所示，圖中1，2，3，…，N-1，N為Lobatto數值積分[10]點.

ξ=2Lx-xmin-1，ξ∈-1，1；L=xmax-xmin.（6）

利用Lobatto數值積分[10]計算式（5）中的積分，

∫xmaxxmin-′δ′+a1′δ+a2δ+fδdx=∫1-1-′δu′2/L2+a1′δ2/L+a2δ+fδdξL2=∑Ni=1Hi-′δu′2/L2+a1′δ2/L+a2δ+fδiL2.（7）

其中，N表示積分點數，右側下標i表示該變量在積分點處的值，Hi為相應積分點對應的積分權系數.需指出，式（7）中導數′均為對標準域坐標ξ求導.結合微分求積法則[11]，

dmfdξmξ=ξi=∑Nj=1Cmijfξj.（8）

將式（7）中所含積分點處的函數值和函數導數值表示為積分點處基本自由度（近似函數值i）的線性加權代數和.式（8）中，Cmij為m階微分求積系數.

物理域坐標系下Lobatto數值積分點處i組成的列向量構成了待求解問題的單元基本自由度，

e=1…i…NT，i=1，…，N.（9）

e右上角（e）即表示一個求積元單元，則

′i=B1ie，′i=B0ie.

（10）

式（10）中，

B1i=C11j…C1ij…C1Nj，j=1，…，NB0i=δ1j…δij…δNj，j=1，…，N.（11）

其中δij為Kronecker符號，即

δij1， i=j；0， i≠j.（12）

則式（7）可進一步表示為

∑Ni=1Hi-′δ′2/L2+a1′δ2/L+a2δ+fδiL2=δeT∑Ni=1Hi-BT1iB1i2/L2+a1iBT0iB1i2/L+a2iBT0iB0iL2e+δeT∑Ni=1HiBT0ifiL2=-δeTKee+δeTFe.

（13）

則式（13）中

Ke=∑Ni=1HiBT1iB1i2/L2-a1iBT0iB1i2/L-a2iBT0iB0iL2Fe=∑Ni=1HifiL2，

（14）

則式（5）最終離散為

∫xmaxxminδ″+a1′+a2+fdx

=-δeTKee+δeTFe

+b.t.=0.（15）

由于變分δe具有任意性，式（15）可轉化為一個線性代數方程組，

Kee=F（e）.

（16）

對于邊界條件b.t.，當β1≠0且β2≠0時，邊界條件可表示為

b.t.=′δxmaxxmin=δNγ2-α2Nβ2-δ1γ1-α11β1.

（17）

可對矩陣Ke、Fe修正如下：

K^e11=Ke11+-α1β1，K^eNN=KeNN+α2β2F^e1=Fe1+-γ1β1，F^eN=FeN+γ2β2.（18）

K

Euclid ExtrazB@ e、F

Euclid ExtrazB@ e其余元素分別與Ke、Fe一致，則式（16）轉化為

K^ee=F^e

（19）

進行求解.

當β1=0且β2=0時，邊界條件可表示為

b.t.=′δxmaxxmin=δN′N-δ1′1（20）

由于β1=0且β2=0，由式（2）和（3）可知，u1、uN為常量，

u1=1=γ1α1，uN=N=γ2α2，（21）

則

δ1=δN=0.（22）

只需修正Ke、Fe，使其滿足式（21）即可.故修正如下：

（e）11=1，（e）1j=0，j=2，…，N；

（e）NN=1，（e）Nj=0，j=1，…，N-1；

（e）=γ1α1，（e）N=γ2α2.（23）

K

Euclid ExtrazB@ e、F

Euclid ExtrazB@ e其余元素分別與Ke、Fe，則式（15）仍轉化為

K^（e）（e）=F^（e）

（24）

進行求解.其余邊界條件，如β1≠0而β2=0，亦可類似處理.

求解代數方程組，即可得e中各元素，物理域中非Lobatto數值積分點處的函數值可通過對i進行拉格朗日插值得到.需要說明的是，對于一般性問題求積元方法僅需在待求解域上劃分一個單元.同時，也可視問題需要進行多個單元拼接求解.有關求積元法的詳細介紹可參考相關文獻[6-9].

3實證分析

選取金融工程計算分析中較為典型的3個實例，采用求積元方法進行計算，驗證求積元方法的準確性和高效性.計算程序采用Matlab軟件編制.

3.1壟斷動態最優化問題

壟斷企業的目標是尋找產品價格P的一條最優路徑，從而在一個有限的時間內[0，T]內實現利潤最大化.假設這個時期足夠短，以保證固定的需求成本函數以及忽略折現的設定是合理的.這個問題可以通過變分法采用一個歐拉方程來描述[12]，

P″-b（1+αb）αhP=-a+2αab+βb2αh2，endprint

P（0）=P0，P（T）=PT.

（25）

該方程是一個二階線性微分方程，其解析解為

P=A1ert+A2e-rt+P，

r=b（1+αb）αh2，P=a+2αab+βb2b（1+αb）.（26）

將邊值條件代入式（26），可得

A1=P0-P-（PT-P）erT1-e2rT，

A2=P0-P-（PT-P）e-rT1-e-2rT.（27）

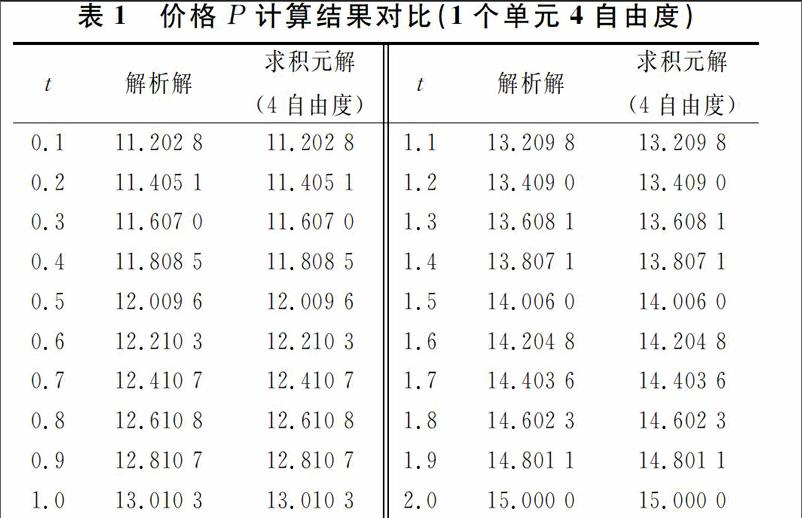
應用求積元方法對該問題在t=[0，2]定義域內進行求解，各時刻t價格P的計算結果與解析解的對比如表1所示.計算相關參數：產出函數中的系數，a=160，b=8，h=100；總成本函數中的系數，α=0.1，β=100；P0=11，PT=15.由表1可見求積元方法僅需劃分1個求積元單元4個積分點（N=4）共計4個自由度即可達到良好的求解精度，小數點后4位有效數字與解析解完全一致，體現出求積元方法的準確性.

3.2幾何布朗運動的首出時

考察幾何布朗運動

dY=aYdt+σYdX

.（28）

在給定標的物價格范圍內的首出時是有實踐意義的.可以得到給定標的物價格偏離某一確定界限的平均時間，進而評估相關雙障礙期權的風險.該問題可以描述為

axu'+σ22x2u''=-1，u（xmin）=0，u（xmax）=0.

（29）

該方程的解析解為

u（x）=1σ2/2-a（ln（xxmin）-1-（x/xmin）1-2a/σ21-（xmax/xmin）1-2a/σ2ln（xminxmax））.（29）

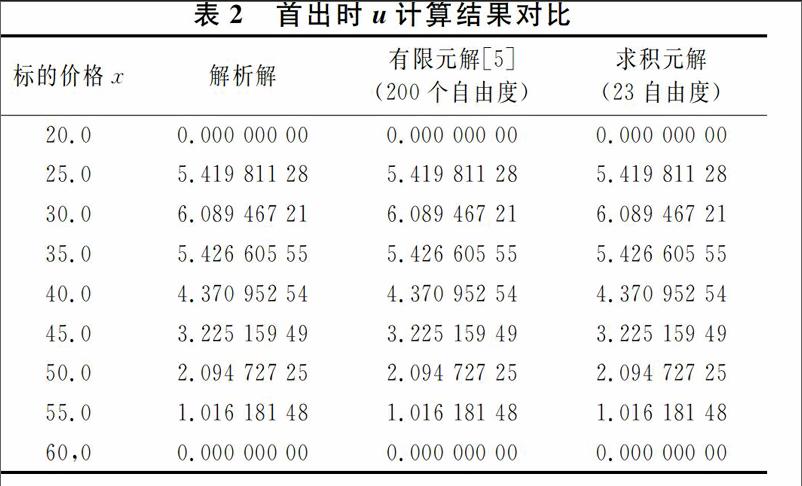
應用求積元方法對該問題進行求解，計算結果與解析解及有限元解[5]的對比如表2所示.計算相關參數為收益率a=0.1，波動率σ=0.2，xmin =20，xmax =60.由表2可見求積元僅需劃分1個單元23個積分點共計23個自由度即可達到良好的求解精度，小數點后8位有效數字與解析解完全一致，而有限元法則需要劃分99個單元共計200個自由度才能達到以上精度，求積元法的計算自由度僅約為有限元法的十分之一，而計算大規模問題時，計算自由度是影響計算機計算效率的重要因素.因此.求積元法相比有限元法具有更為高效的特點.

3.3對流占優問題

對流占優問題在金融工程中具有很強的實際意義[13]，比如當標的物價格較低且（/或）波動率較低時，股票期權、外匯期權的定價將成為對流占優問題.以如下的邊值問題

-ku″+u′=0，u（0）=0，u（1）=1.

（30）

為例進行說明，當k減小時，該微分方程橢圓型方程特征逐漸減弱，雙曲型方程特征逐漸增強.此時，由于“對流項”u′主要影響方程的特性，該問題稱為對流占優問題.

該方程的解析解為

u（x）=1-e（x/k）1-e（1/k）.

.（31）

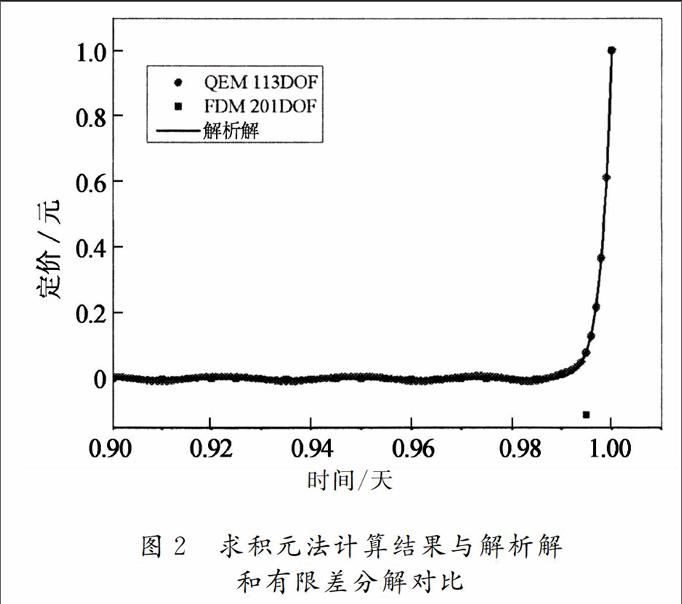
應用求積元方法對該問題進行求解，計算結果與解析解及有限差分解的對比如圖2所示.計算相關參數為k=0.002.由圖2可見，該問題的解析解曲線具有很強的非線性，表現為在[0，0.99]范圍內非常平緩，而在[0.99，1]范圍內急劇上升.

本例中求積元方法（QEM）共劃分8個單元，每個單元采用15個積分點，共計113個自由度，達到了較好的計算結果.而有限差分法（FDM）在劃分單元數較少時，計算結果出現了明顯的震蕩[5]，即使劃分200個單元（201個自由度），也存在震蕩現象（如圖2所示）.若采用有限元方法，得到滿意的計算結果也需要200個自由度以上[5].相比有限差分法和有限元法，求積元法的計算自由度縮減了近一半，再次體現出準確高效的特點.

4結論

針對金融工程計算領域的靜態一維問題，將求積元方法的應用領域從線性自伴隨微分方程的求解拓展到非自伴隨微分方程的求解.首先，基于Galerkin加權殘值法思想建立了相應的求積元單元；之后，選取了三個典型問題進行編程求解計算，并與解析解、有限差分解和有限元解分別進行了比較.

計算結果表明，相比有限元方法和有限差分法，求積元方法在得到相同精度計算結果的同時，大幅減少了自由度數，提高了計算效率.對于一般性問題，僅需劃分一個單元，也可視問題的復雜性進行多單元拼接求解.是一種準確、高效和靈活的數值方法.用于金融工程領域的靜態一維問題計算分析有較大的優勢，可進一步用于該領域動態問題（期權定價問題）、二維問題的計算分析.

參考文獻

[1]M ROSS. An Elementary Introduction to Mathematical Finance.[M]. London： Cambridge University Press， 2011.

[2]郭宇權. 金融衍生產品數學模型[M].北京： 世界圖書出版公司北京公司， 2010.

[3]科森多爾. 隨機微分方程[M]. 北京： 世界圖書出版公司北京公司， 2006.

[4]蔣致遠， 張跳， 龔閃閃. 基于拉普拉斯變換有限差分方法的B-S期權定價[J]. 經濟數學，2014， 31（3）： 18-22.

[5]T JURGEN. Financial engineering with finite elements[M]. Chichester： John Wiley & Sons Ltd， 2005.

[6]H ZHONG， T YU. A weak form quadrature element method for plane elasticity problems[J]. Applied Mathematical Modelling， 2009， 33（10）： 3801-3814.

[7]H ZHONG， M GAO. Quadrature element analysis of planar frameworks[J]. Archive of Applied Mechanics， 2010， 80（12）： 1391-1405.

[8]Z SHEN， H ZHONG. Static and vibrational analysis of partially composite beams using the weakform quadrature element method[J]. Mathematical Problems in Engineering， Vol. 2012， Article ID 974023， 23 pages.

[9]Z SHEN， H ZHONG. Nonlinear quadrature element analysis of composite beams with partial interaction. Australian Journal of Mechanical Engineering， 2013， 11（1）： 45-52.

[10]P DAVIS， P RABINOWITZ. Methods of numerical integration. [M]. Orlando： Academic Press， 1984.

[11]C SHU. Differential quadrature and its application in engineering[M]. London： SpringerVerlag， 2000.

[12]A CHIANG. Elements of Dynamic Optimization [M]. New York： McGrawHill， Inc，1992.

[13]R SEYDEL. Tools for Computational Finance [M]. Berlin： Springer， 2002.endprint