帶觀察時的跳服從Erlang（n）分布的對偶模型的紅利貼現問題＊

談普林

（武漢大學 數學與統計學院，湖北 武漢 430072）

1 引 言

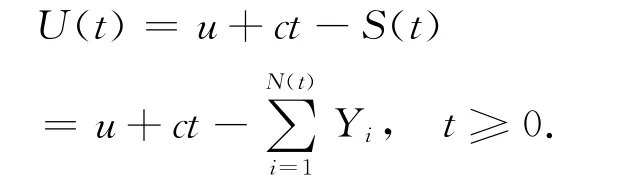
其中，u＝U（0）≥0為初始盈余，c為保費率即收入率，S（t）表示保險公司的總索賠額即支出，一般為復合泊松過程．在研究一般公司的盈余過程時發現公司的支出是持續的，收入是隨機的．通過改進得到了對偶風險模型，可參見 Avanzi等人（2007）［1］，Avanzi 和 Gerber （2008）［2］，Gerber 和 Smith（2008）［3］的工作．在對偶風險模型中，t時刻的盈余表示為

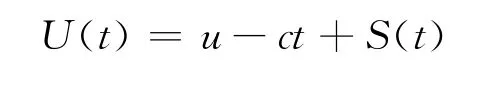
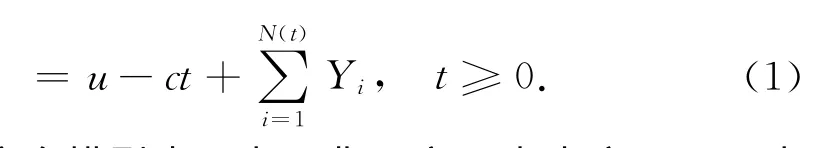
在這個模型中c表示費用率即支出率，S（t）表示總收益，其中N（t）和Yi相互獨立．假設是非負的獨立同分布隨機序列，密度函數為p（y）且期望為μ＝E（Y1）．

De Finetti（1957）［4］首次提出在風險模型中考慮分紅策略，認為這個過程更貼切實際情形．分紅策略一般有兩種．一種是邊值策略，即當盈余過程超過給定的邊值時，紅利才分發且發放超過邊值部分的全部．另一種是閥值策略，相同的是在盈余過程超過給定閥值才分發紅利，不同的是當超過閥值時，分紅率是一個固定的常數．Avanzi等人（2007）［1］研究了在邊值策略下對偶風險模型的最優紅利問題，Avanzi等人（2013）［5］研究了在邊值策略下帶觀察時的對偶風險模型的破產概率和貼現紅利，Ng（2009）［6］研究了在閥值策略下對偶風險模型的貼現紅利．關于收益過程，這些文章都是基于復合泊松過程討論的，在模型的進一步推廣時，收益改用更新過程來研究．Li和 Garrido（2004）［7］研究了復合更新過程（索賠時間間隔即跳過程服從Erlang（n）分布）下風險模型的破產概率，Albrecher等人（2005）［8］則給出了跳服從廣義Erlang（n）分布的貼現紅利任意階矩，Eugenio等人（2014）［9］在跳服從Erlang（n）分布下把模型推廣到對偶情形并討論破產概率和貼現紅利問題，Yang和Sendova（2014）［10］在此基礎上推廣到廣義Erlang（n）分布．關于收益過程采用復合更新過程來描述已經有很多文章了，但是他們都沒考慮帶觀察時的情形．基于此，考慮在邊值策略下帶觀察時跳服從Erlang（n）分布的對偶風險模型．不同于Peng等人（2013）［11］（紅利分發和破產均在觀察時發生）的研究，而是類似于Avanzi等人（2013）［5］紅利分發只在觀察時發生而破產可能是在任意時刻發生的（即盈余U（t）＜0就破產）．

本文的結構如下：在第二部分，介紹具體模型和定義．在第三部分第一節，給出紅利期望貼現函數V（u；b）滿足的微積分方程組．在第三部分第二節，利用第三部分第一節結果討論收益額服從PH（m）分布時的紅利期望貼現函數，并給出V（u；b）的解析解．在第三部分第三節，給出觀察時及收益額均服從指數分布時V（u；b）的具體求解．在第四部分第一節，給出跳退化為指數分布時V（u；b）的顯示解及其極限，并與 Avanzi等人（2007）［1］和 Avanzi等人（2013）［5］的結果進行比較．在第四部分第二節，給出跳服從Erlang（2）分布時，V（u；b）的數值舉例．

2 模型及定義

根據式（1），｛U（t），t≥0｝ 的破產時間定義為τ＝inf ｛t≥0：U（t）≤0｝ ．計 數 過 程N（t）＝min ｛k：T1＋T2＋…＋Tk＋1＞t｝是 一 個 更 新 過程，是正的獨立同分布隨機序列（T定義i為第（i－1）次產生收益到第i次產生收益的時間間隔）．

假定Ti（i＝1，2，…）服從 Erlang（n）分布，即密度函數為！．假設公司是可盈利的，即c＜μ／E（Ti）?cn＜λμ．

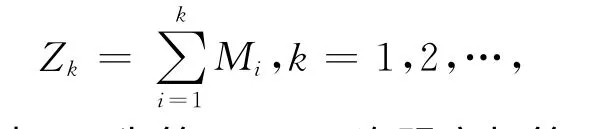
其中Mi為第（i－1）次觀察與第i次觀察所經歷的時間，｛Mi，i≥1｝獨立同分布且分布函數為F（x），并假設與 ｛Yi，i≥1｝以及相互獨立．進一步，假設邊值策略下紅利分發只發生在時刻，即任意時刻Zk盈余超出邊界值b（＞0），則超出部分全部作為紅利分發．

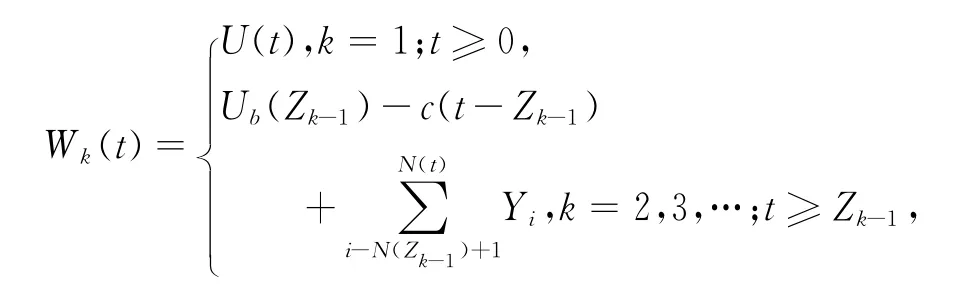
以及對k＝1，2…，

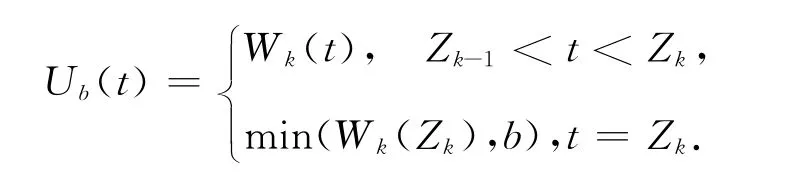
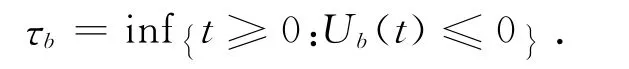
類似地定義當前模型的破產時間為令Kb＝則Kb表示直到破產為止總共發生觀察的次數．

紅利期望貼現函數可定義為

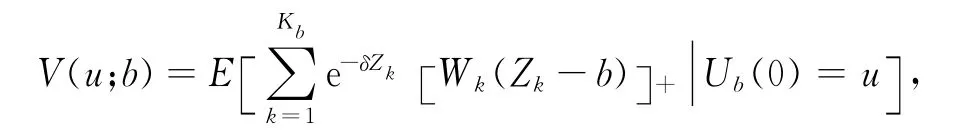
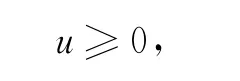
其中a＋＝max（a，0），δ為貼現力．假設V（u；b）線性有界．圖1給出了盈余過程的變化軌跡圖．

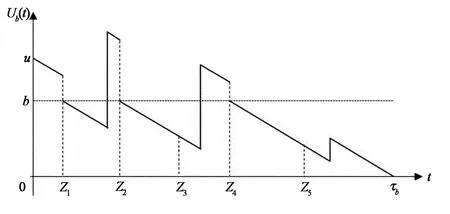
圖1 盈余過程 ｛Ub（t），t≥0｝ 的變化軌跡圖

3 跳服從Erlang（n）分布時V（u，b）的求解

由Erlang（n）是n個獨立同分布的指數分布之和，把跳過程分成n步，前n－1步跳的大小為0，最后一步跳的密度函數為p（y），y≥0．第i步跳的紅利期望貼現函數記為Vi（u；b），i＝1，2，…，n，且假設在b點連續．對i＝1，2，…，n，定義

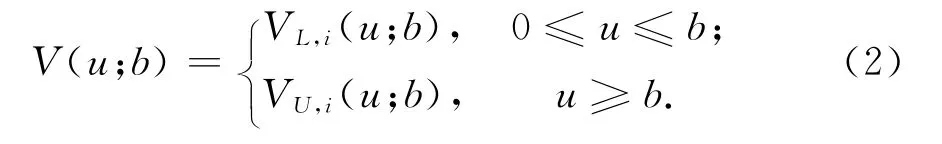
3．1 V（u；b）的微積分方程組

定理1Vi（u；b），i＝1，2…，n，滿足下面的微積分方程組

當i＝1，2，…，n－1時，

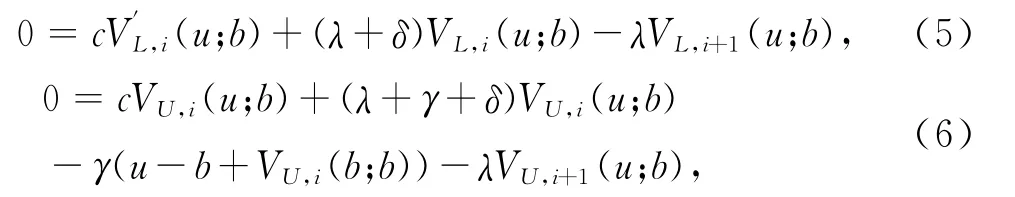
當i＝n時，

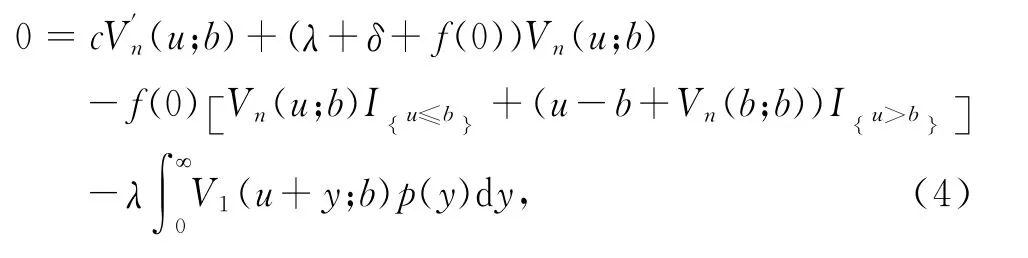
Vi（u；b），i＝1，2，…，n滿足邊界條件

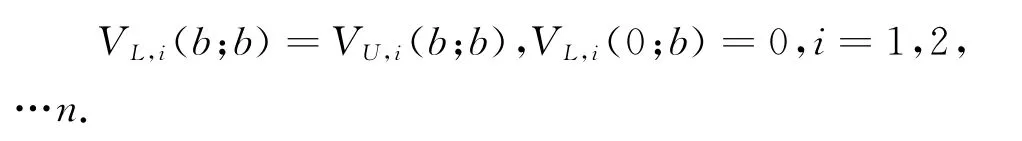
其中f（x）是觀察時分布函數F（x）的密度函數．

證明 對u≥0，在每一步i足夠小的時間區間［0，h］中考慮跳和觀察兩個事件，注意到這兩個事件是相互獨立的，在這個區間中根據它們是否發生以及發生的先后關系得到下面的等式．

當i＝1，2，…n－1時，跳的大小為0，于是

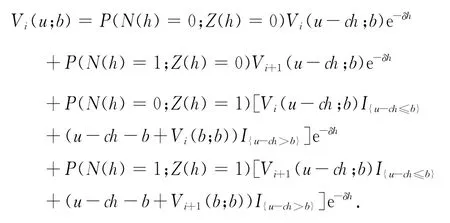
對上式代入密度函數f（x），利用泰勒展式得到

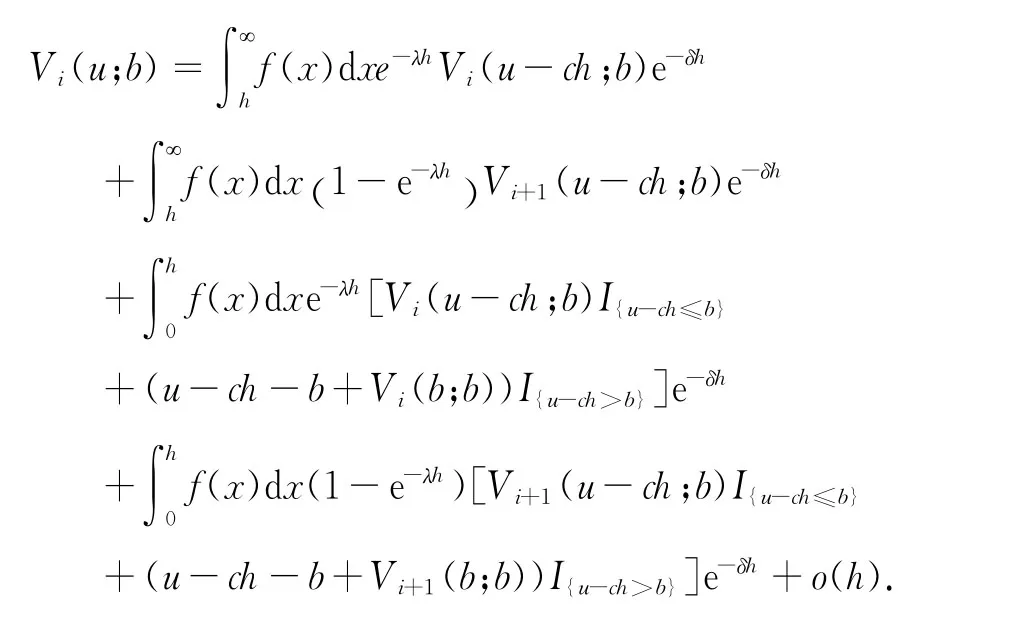
可以看出上面等式右邊第四項趨向于o（h2）．于是，對上式兩邊同時除以h，并令h→0即可得式（2）．

當i＝n時，跳的大小（即收益額）的密度函數為p（y），y≥0，類似可推得

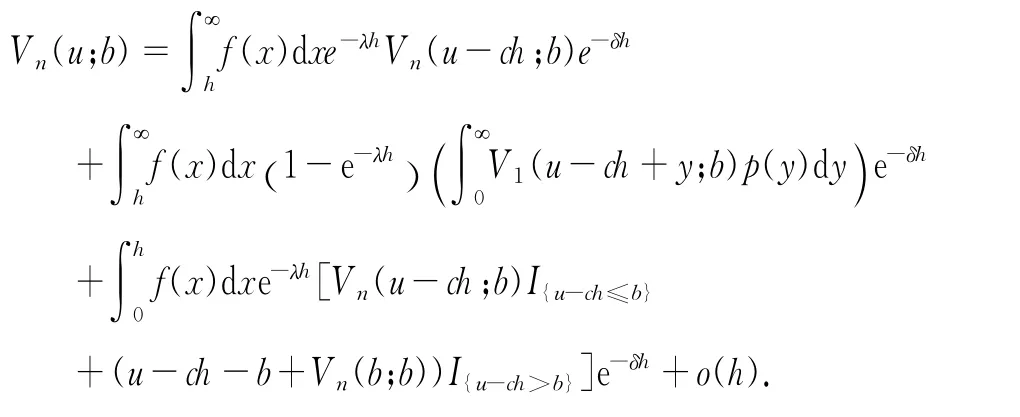
由上式同理可證式（3）成立，邊界條件由初始值假設和連續性假設得到．

當f（x）＝，x＞0時，由定理1可以得到下面的推論．

推論1Vi（u；b），i＝1，2，…，n滿足下面的微積分方程組

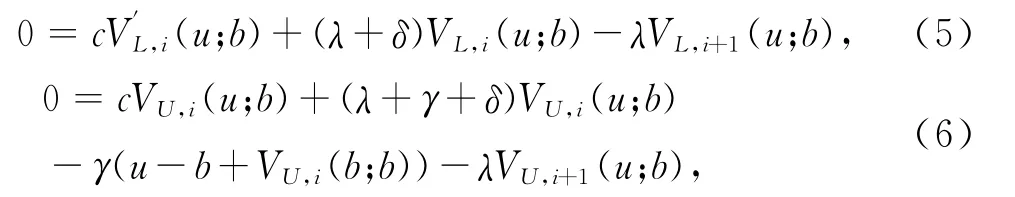
當i＝n時，

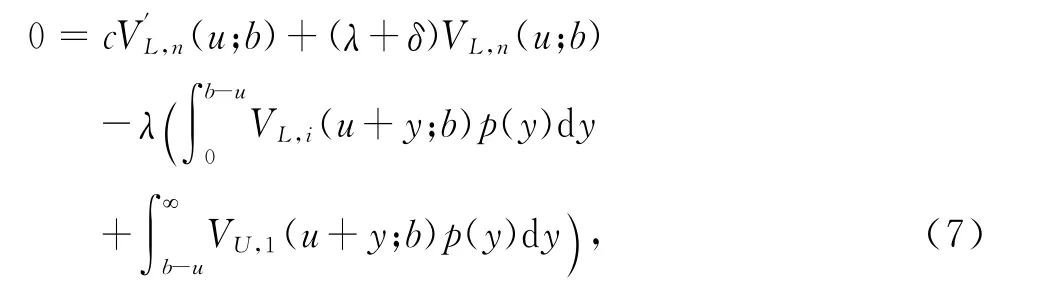
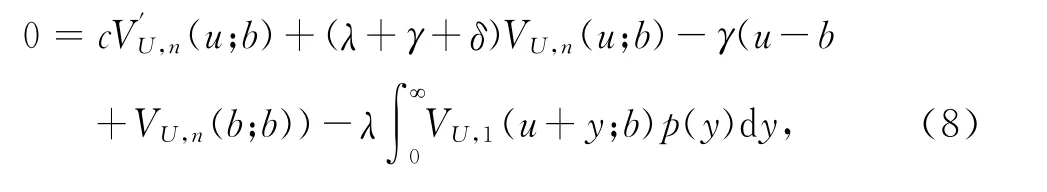
Vi（u；b），i＝1，2，…n滿足邊界條件

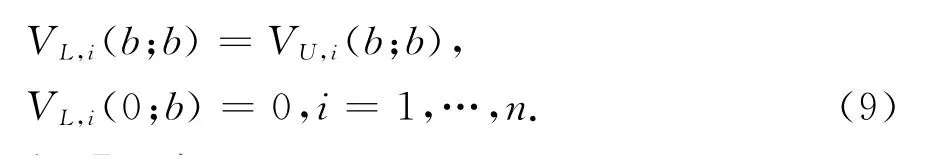
證明 由于f（0）＝γ，并把式（2）代入定理1即可證明推論成立．

注1 在推論1中，i＝n時發生了跳，由連續性假設可知令u＝b，有（b；b）＝（b；b），該條件在后面求解V（u；b）時將被應用．

注2 顯然V（u；b）≡V1（u；b），因此只需求解（u；b）和VL，1（u；b）．

3．2 觀察時和收益額分別服從指數和PH（m）

分布時V（u；b）的求解

假定Erlang（2）為PH（m）分布，其中PH（m）定義可參見 Eugenio等人（2014）［9］的5．2部分．

3．2．1VU，1（u；b）的解析解

由Eugenio等人（2014）［9］的定理5．2知p（xu）的零化因子為qΒ（－Du），其中Du＝?／?u，qΒ（y）＝Det（Β－yΙm）．考慮qΒ（－Du）的多項式形式：

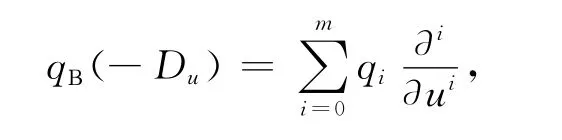
其中qi，i＝0，1，…，m，是常數．

對式（8）做變換y＋u＝x得到

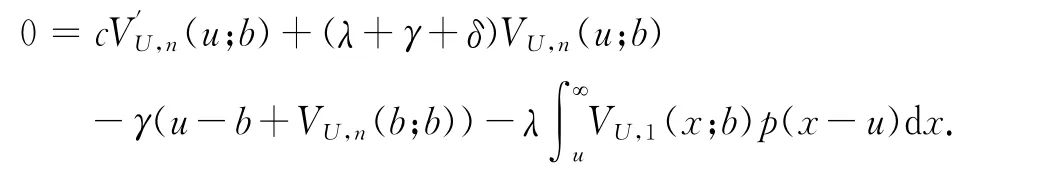
對上式作用qΒ（－Du）＝得到

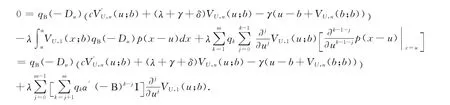
對上式求偏導?／?u得到

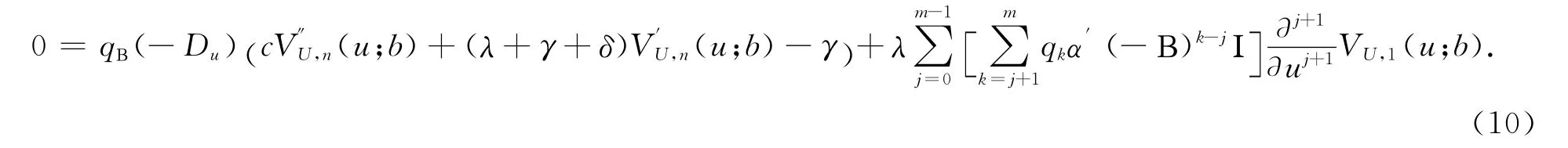
對 式（6）求偏導?／?u，當i＝1，2，…，n－1時有

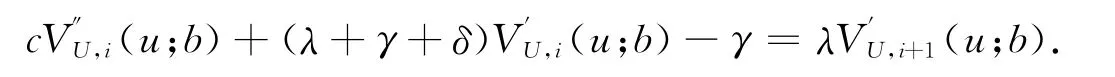
上式為遞歸形式，令?／?u＝Du，可知

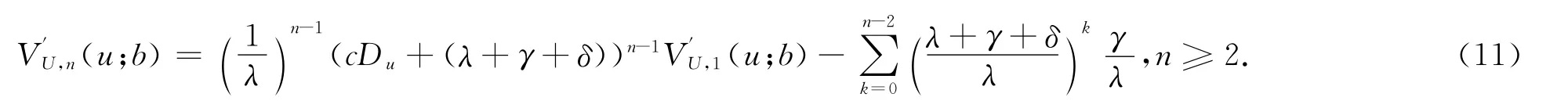
把式（11）代入式（10）式整理可得

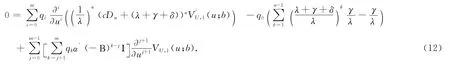
上式也可以歸納為

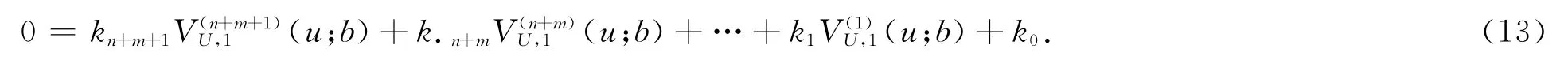
故VU，1（u；b）的解析解為

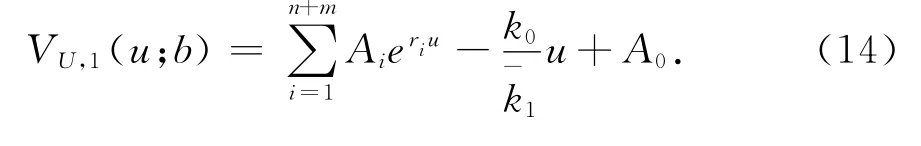
3．2．2VL，1（u；b）的解析解

由式 （5）可得，

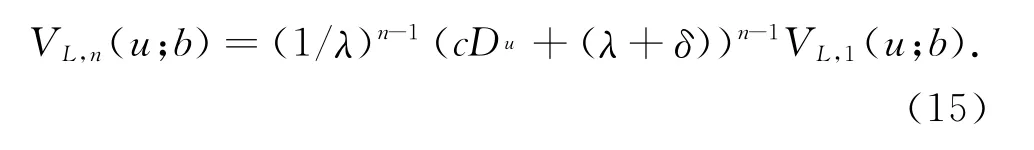
先對式（7）做變換y＋u＝x，再作用qΒ（－Du）得到

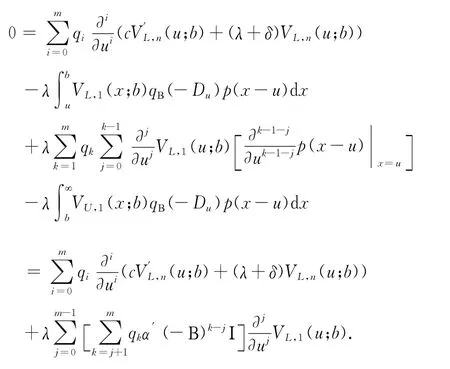
將式（15）代入上式整理可得到

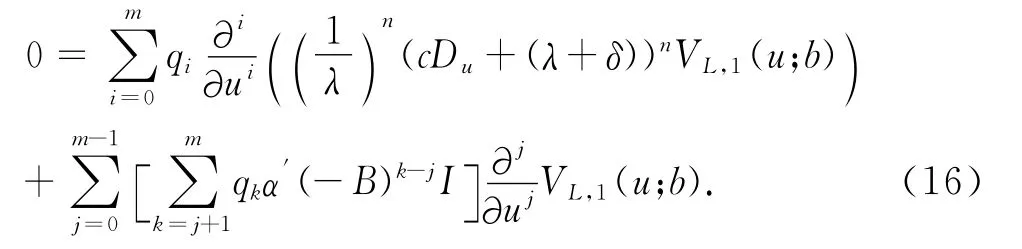
注意到對照Eugenio等人（2014）［9］的 （5．7）式，發現與上式是相同的．因此得到VL，1（u；b）的解析解為

3．3 觀察時及收益額均服從指數分布時V（u；b）的求解

在PH（m）中令m＝1，即p（y）＝βe－βy，y＞0，為指數分布，探討VU，1（u；b）和VL，1（u；b）顯示解的具體求解過程．

3．3．1VU，1（u；b）的解析解

由于此時p（y）為指數分布，整理式（12）得到

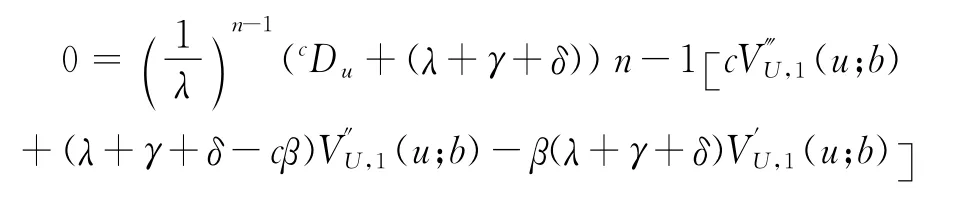
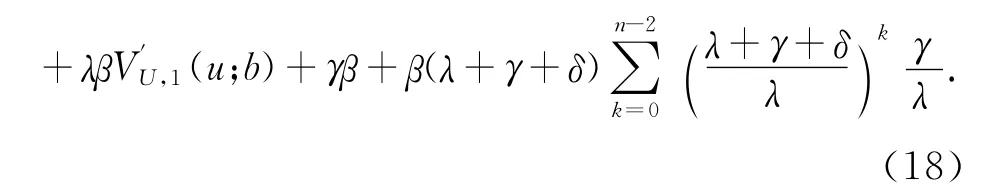
上式經過展開可以得到關于VU，1（u；b）的n＋2次微分方程，即

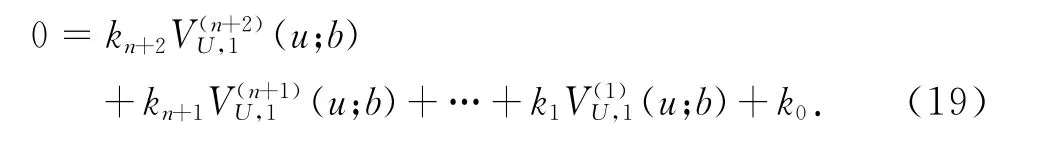
其中k0，k1，…，kn＋2是由λ，γ，δ，β，c組成的常數．令

則當i＝1，2，…，n＋2時，

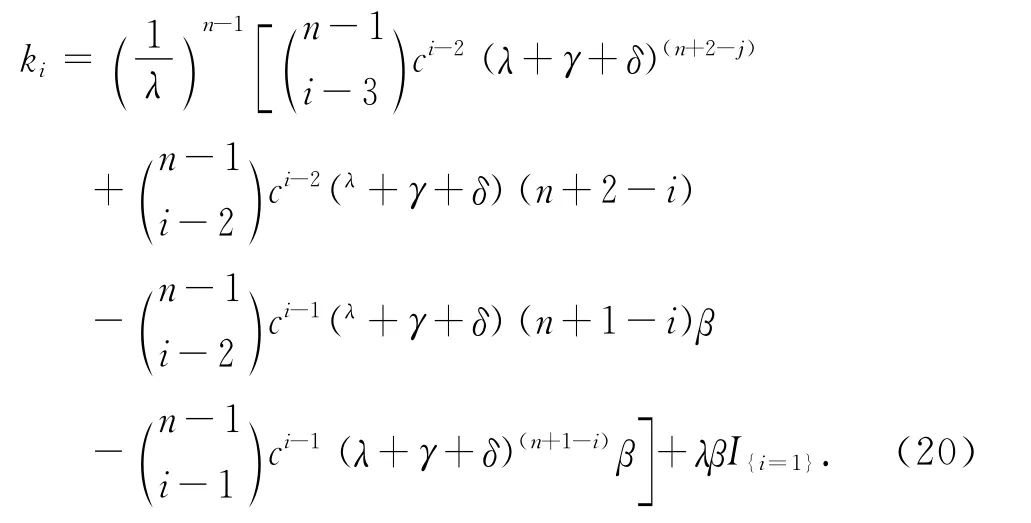
當i＝0時

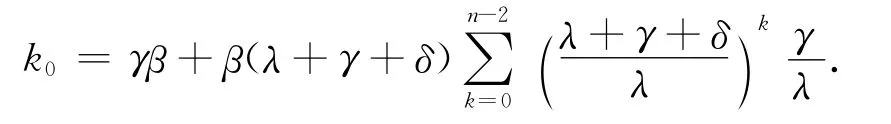
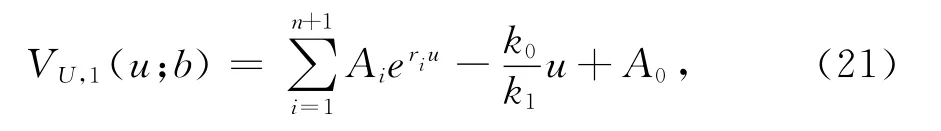
其中Ai為待求系數，ri為下面式（22）的根，

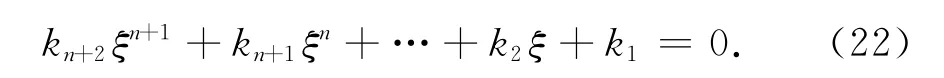
引理1 方程式（22）有n個實部為負的根，且有唯一的正根．

證明 首先令f（ξ）＝＋…＋下面計算f（ξ），由式（20）可得

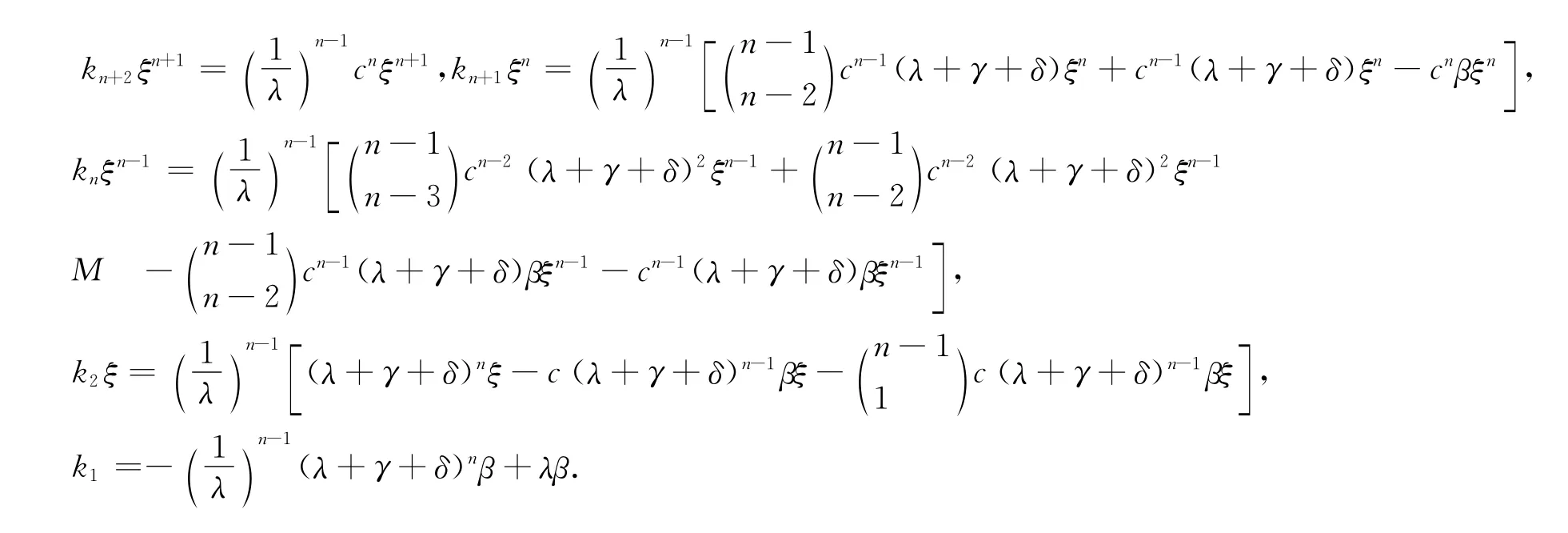
注意到上面系列等式左邊相加等于f（ξ），右邊相鄰兩式正負依次組合在一起提取公共項（1／λ）n－1（ξ－β）然后相加即得二項式展開形式．

經過整理可得

故存在一個正根．

令f（－ξ）＝0，整理后得到

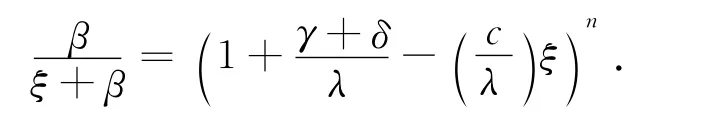
因為參數為β的指數分布的拉普拉斯變換等于，所以有的拉普拉斯變換）．根據Eugenio等人（2014）［9］第三部分的討論，可知方程22有n個實部為負的根．又因為方程22共有n＋1個根，故有唯一的正根．

由引理1，假設是唯一的正根，根據V（u；b）線性有界假設，可得＝0．對VU，1（u；b）還有A0，A1，．．．，An共n＋1個待求系數，將在后文給出具體的求解過程．

3．3．2VL，1（u；b）的解析解

整理 式（16）得到

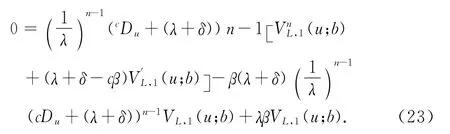
把 式（23）改寫成式 （24）

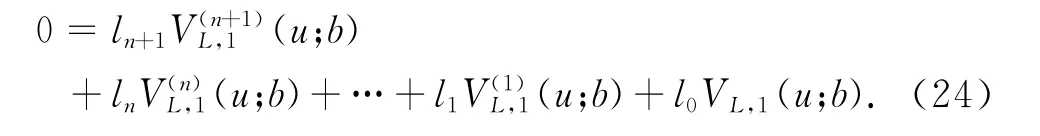
其中l1，i＝0，1，…，n＋1，可寫成下面形式

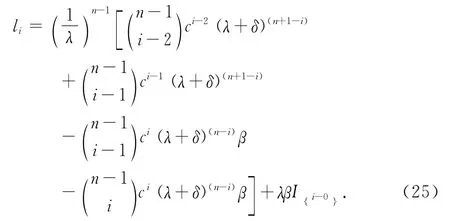
于是，VL，1（u；b）的形式解為

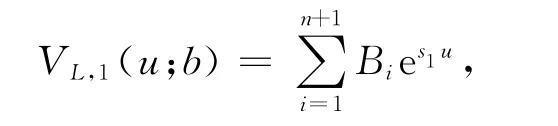
其中，i＝1，2，…，n＋1，是下面方程的根

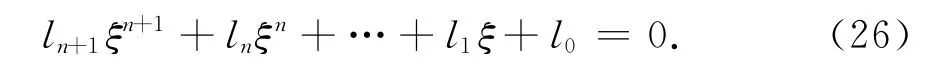
注意到有A0，A1，…，An，B1，B2，…，Bn＋1共2n＋2個待求系數，需要2n＋2個方程．首先，根據推論1的邊界條件共得到2n個方程．其次，利用注1得到一個方程．最后，把VU，1（u；b）和VL，1（u；b）的解析解以及 式（15）代入 式（7），根據的系數等于零得到第2n＋2個方程．

4 紅利期望貼現函數V（u；b）的求解實例

現在討論觀察時及收益額均服從指數分布時V（u；b）的顯示解和數值舉例．其中，在4．1中考慮跳服從指數分布時V（u；b）的顯示解以及γ→ ∞時V（u；b）的極限．在4．2中考慮跳服從 Erlang（2）分布，并給出相應的數值舉例．在不引起歧義的情況下，令V1（u；b）＝VL，1（u；b），

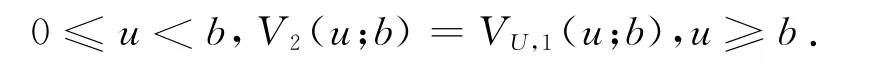
4．1 跳及觀察時均服從指數分布時V（u；b）的求解

假設跳服從Erlang（1）分布，即指數分布，則式（7）改寫為

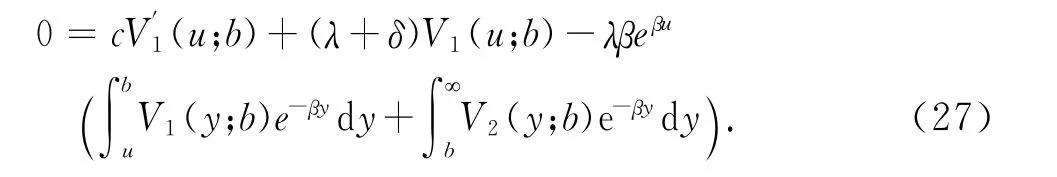
根據 式（21）得

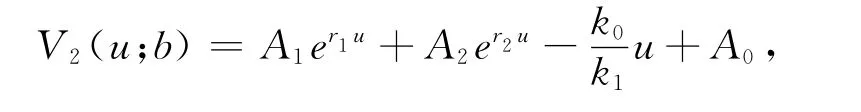
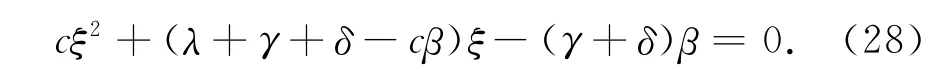
由線性有界假設知A2＝0，因此

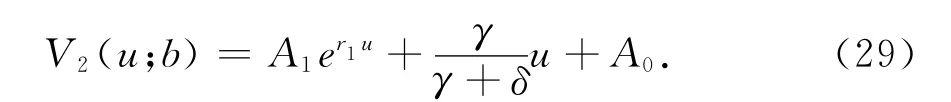
同理可得V1（u；b）的解析解為

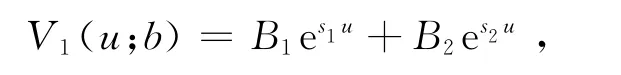
其中，s1，s2是下面方程的兩根

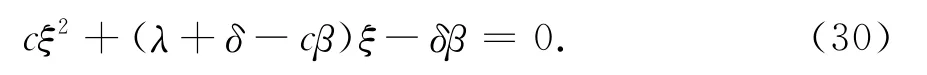
根據V1（0；b）＝0，可推得

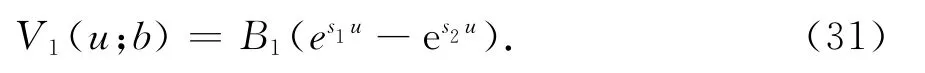
由邊界條件V1（b；b）＝V2（b；b）和（b；b）＝（b；b）以及 式（29）和（31）得

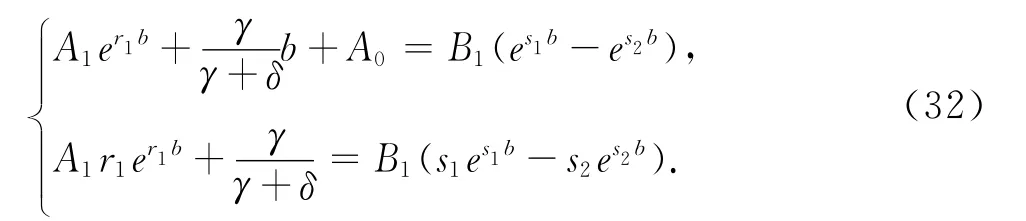
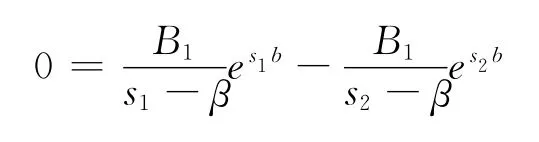
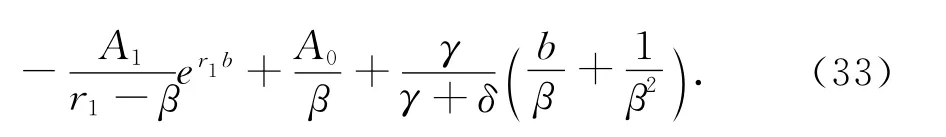
于是，由 式（32）和式（33）求得V1（u；b），V2（u；b）

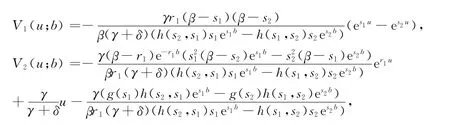
其中g（x）＝βbr1x＋r1x－β（r1＋x），h（x，y）＝（β－x）（y－r1）．

注3 將上述結果與 Avanzi等人（2013）［5］的（4．2）式對比，當－ργ＋δ＝r1時，由r1和s1分別是方程（28）和 （30）的根，可得下面的等式

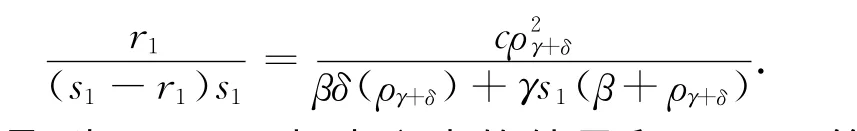
于是，當n＝1時，本文中的結果和Avanzi等人（2013）［5］的（4．2）式是一致的．

注4 由求解r對應的方程可得出＝－11．對V1（u；b），0＜u≤b，取極限得到

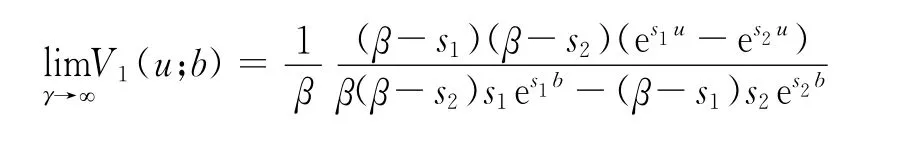
分別為

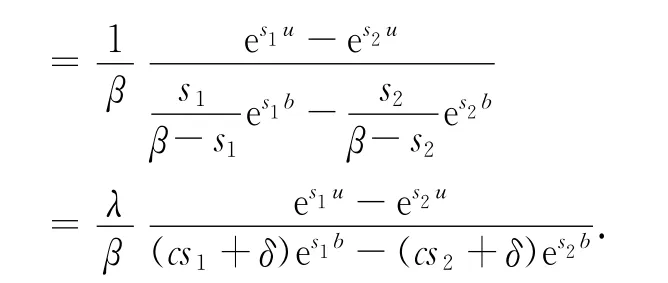
對上述結論做數值模擬，見圖2、圖3和表1、表2．其中，圖2和圖3分別表示固定b在不同u值下隨著γ趨向無窮V1（u；b）的極限值．對比表1和表2會發現相同u值下，V1（u；b）隨b的增大而減小．

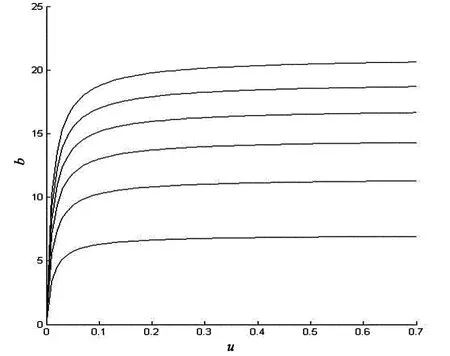
圖2 c＝0．8，λ＝1，δ＝0．01，β＝1，b＝12

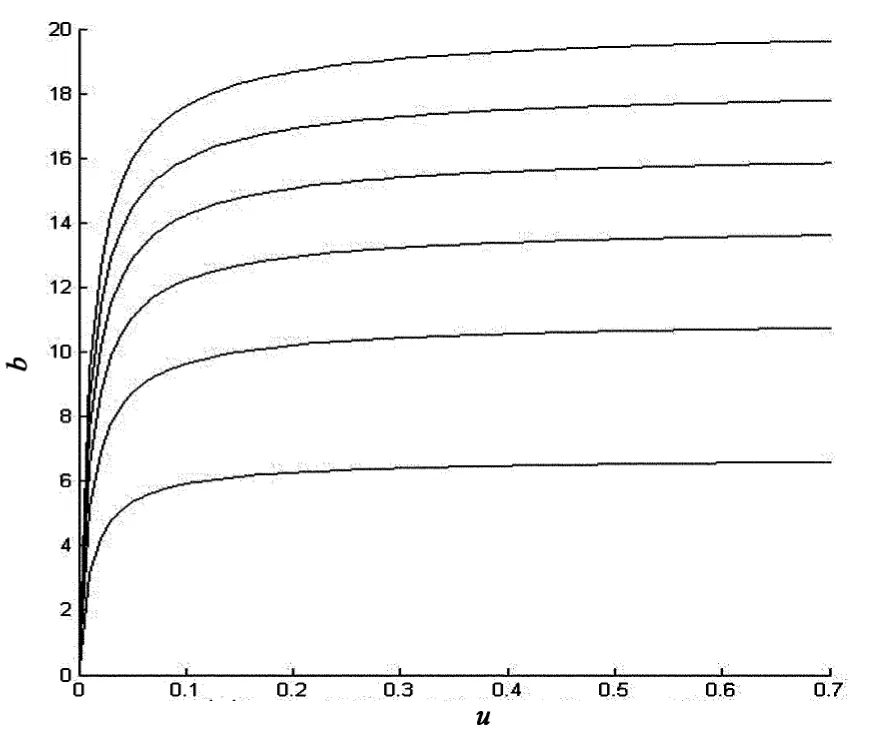
圖3 c＝0．8，λ＝1，δ＝0．01，β＝1，b＝14

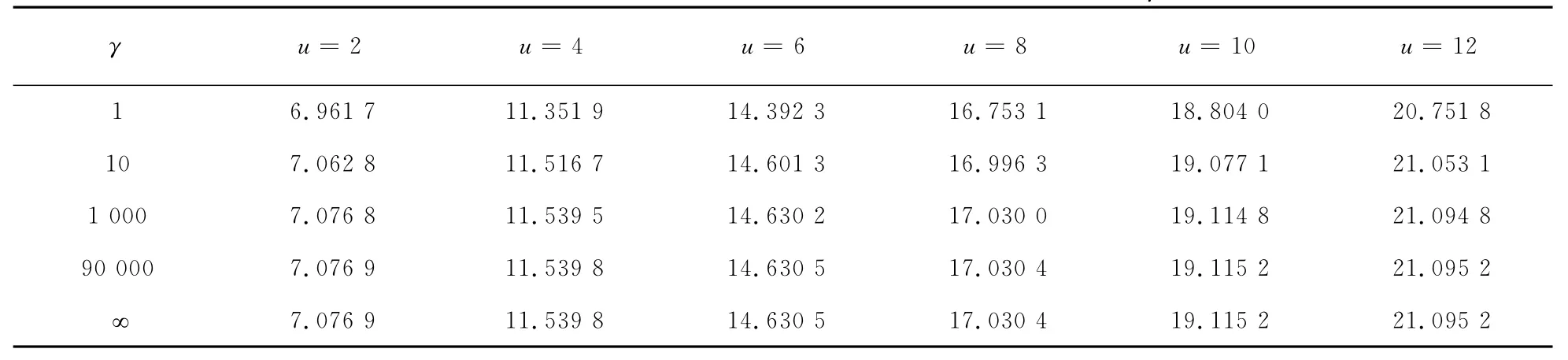
表1 參數γ和u對V1（u；γ）的影響，其中c＝0．8，λ＝1，δ＝0．01，β＝1，b＝12

表2 參數γ和u對V1（u；γ）的影響，其中c＝0．8，λ＝1，δ＝0．01，β＝1，b＝14

4．2 跳和觀察時分別服從Erlang（2）和指數分布時V（u；b）的數值舉例

跳服從Erlang（2）分布時，由第三部分第三節的討論可知

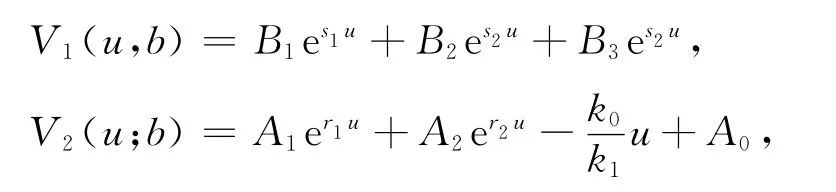
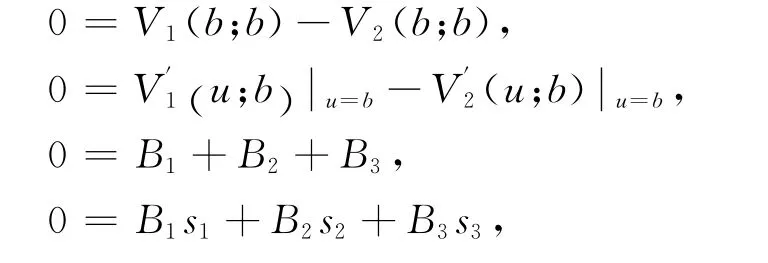
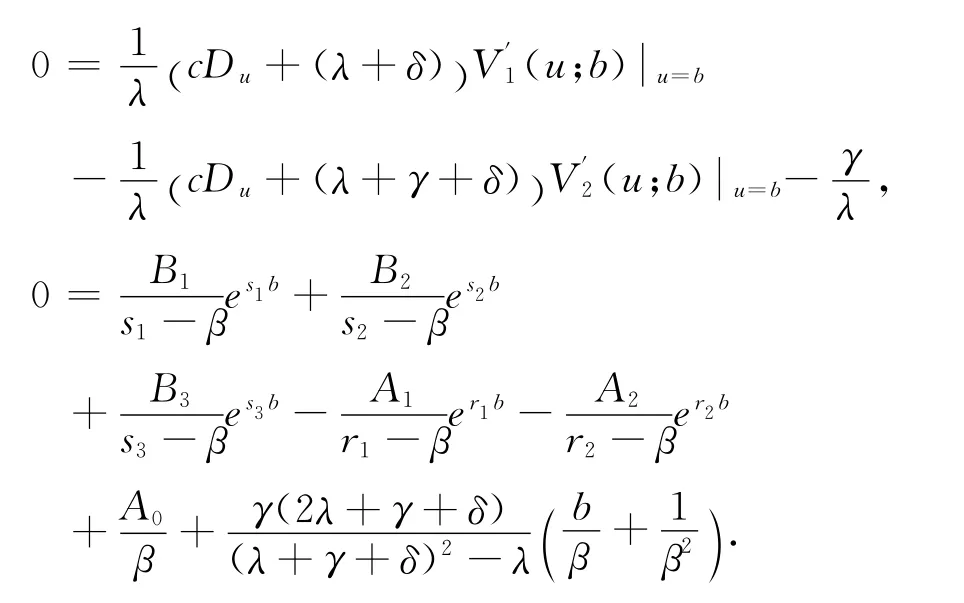
例 令c＝0．8，λ＝2，δ＝0．05，β＝1求得根s1＝0．1515，s2＝－0．5625，s3＝－3．7140和r1＝－3．9374，r2＝－6．0069．由上面的方程組可以看出待求系數與b相關，即給定b的值就可以求出相應的系數，故有

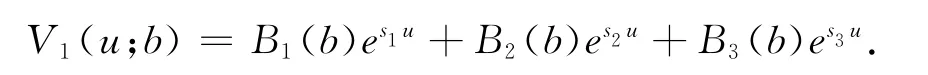
經過數值計算得到圖4和表3，圖表中的數據說明總體上V1（u；b）隨著b的增大而減小，隨著u的增大而增大．

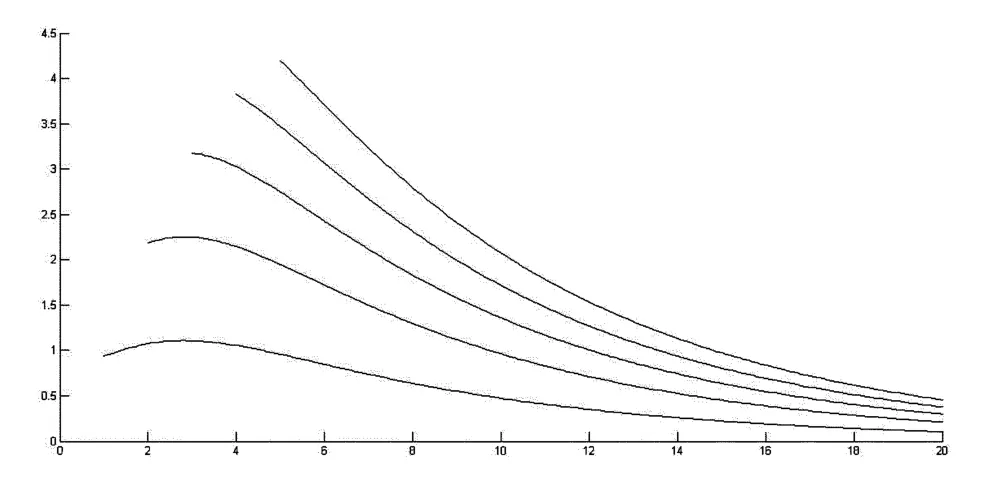
圖4 關于b，V1（u；b）的函數圖像，u＝1，2，…，5

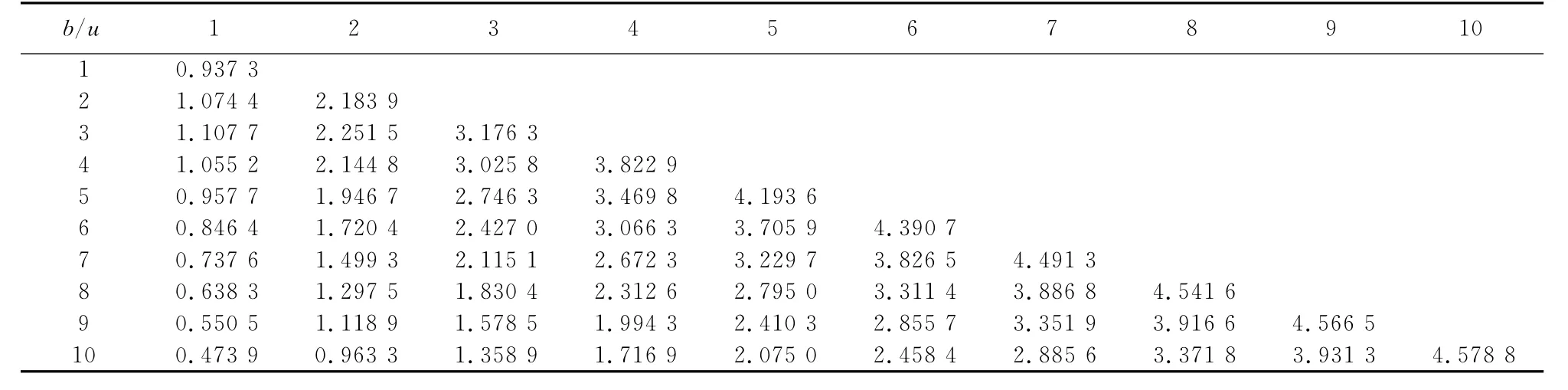
表4 參數γ和u對V1（u；γ）的影響，其中c＝0．8，λ＝2，γ＝2，δ＝0．05，β＝1

5 結 論

建立了邊值策略下帶觀察時的跳服從Erlang（n）分布的對偶風險模型，通過求解隨機微分方程組給出了紅利期望貼現函數V（u；b）的解析解．相比較于傳統的風險模型用于研究保險公司的盈余過程，而其對偶模型適用于一般公司．對比Eugenio等人（2014）［9］研究Erlang（n）分布，利用更新過程的無記憶性，把Erlang（n）分布分成n個階段來討論．紅利分發只在觀察時發生的假設和使用更一般的更新過程來研究使研究結果更加具有現實意義和一般性．對于觀察時為指數分布等其它情形，可以進一步使用其他分布來研究．

［1］B AVANZI，H U GERBER，E S W SHIU．Optimal dividends in the dual model［J］．Insurance：Mathematics and Economics，2007，41（1）：111－123．

［2］B AVANZI，H U GERBER．Optimal dividends in the dual model with diffusion［J］．ASTIN Bulletin，2008，38（2）：653－667．

［3］H U GERBER，N SMITH．Optimal dividends with incomplete information in the dual model［J］．Insurance：Mathemat－ics and Economics，2008，43（2）：227－233．

［4］B DE FINETTI．Su un＇impostazione alternatival dell teoria colletiva del rischio［C］．／／Proceedings of the Transactions of the XV International Congress of Actuaries，1957，2（2）：433－443．

［5］B AVANZI，E C K CHEUNG，B WONG，etal．On a periodic dividend barrier strategy in the dual model with continuous monitoring of solvency［J］．Insurance：Mathematics and Economics，2013，52（1）：98－113．

［6］A C NG．On a dual model with a dividend threshold［J］．Insurance：Mathematics and Economics，2009，44（2）：315－324．

［7］SM LI，J GARRIDO．On ruin for the Erlang（n）risk process［J］．Insurance：Mathematics and Economics，2004，34（3）：391－408．

［8］H ALBRECHER，M M CLARAMUNT，M MARMOL．On the distribution of dividend payments in a Sparre Andersen model with generalized Erlang（n）interclaim times［J］．Insurance：Mathematics and Economics，2005，37（2）：324－334．

［9］V R EUGENIO，M R C RUI，D E ALFREDO．Some advances on the Erlang（n）dual risk model［J］．ASTIN Bulletin，2014，45（1）：127－150．

［10］C YANG，K P SENDOVA．The ruin time under the Sparre－Andersen dual model［J］．Insurance：Mathematics and Economics，2014，54（1）：28－40．

［11］D PENG，D H LIU，Z M LIU．Dividend problems in the dual risk model with exponentially distributed observation time［J］．Statistics and Probability Letters，2013，83（3）：841－849．