基于客流影響的城軌交通列車運行調整研究

曹繼茹，王小敏，陳建譯

（1.西南交通大學 信息科學與技術學院，成都 610031；2.廣州鐵路（集團）公司 電務處，廣州 510088）

基于客流影響的城軌交通列車運行調整研究

曹繼茹1，王小敏1，陳建譯2

（1.西南交通大學 信息科學與技術學院，成都 610031；2.廣州鐵路（集團）公司 電務處，廣州 510088）

列車運行調整是城軌交通調度指揮行車的重要內容，但存在約束條件多、搜索空間大、可行解范圍小等問題，往往難以獲得滿意解。為解決該問題，結合城軌交通列車運行特點，本文建立基于客流量影響的列車運行調整優化模型，采用改進粒子群算法進行求解。通過與遺傳算法、粒子群算法對比，驗證本文模型及算法的有效性。

列車運行調整；客流量；粒子群算法

城市軌道交通的運營特點包括追蹤間隔短，行車密度高。基于通信的列車運行控制（CBTC）系統采用的移動閉塞技術，縮小了列車追蹤間隔，一旦列車發生晚點就容易影響其他列車的正常運行，使列車運行秩序發生紊亂。列車運行調整問題的核心任務就是當運行中的列車發生晚點或者被外界條件干擾偏離了計劃運行圖時，能夠使列車盡快恢復到圖定時刻，并解決當前列車晚點和晚點傳播的影響。

列車運行過程中常見的影響因素有停站時間、區間運行時間、追蹤間隔等。在實際運營中，列車發生晚點時發車間隔將會增大，容易導致乘客在站臺等待時間加長而客流積壓的情況，此時車門可能無法按時關閉[1]。為保證乘客能正常搭載列車，需要適當延長停站時間，而客流量較少的車站，停留過長時間會造成時間損耗。因此，客流量是影響列車運行調整的重要因素。本文將根據客流量對停站時間的影響，建立基于客流量的列車運行調整優化模型。

1 調整模型

1.1 列車運行調整的目標函數

列車運行調整的基本目標是按照計劃運行圖組織行車，讓列車盡快恢復到圖定運行時間，提高正點率。所以本文采取實際運行圖和計劃運行圖之間的偏差最小為調整目標函數。

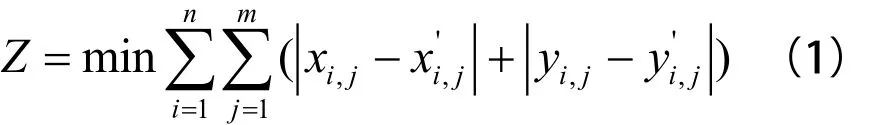
其中，n為列車調整區段內的總列車數；m為調整區段內的總車站數；為列車i在車站j的實際到站時間；為列車i在車站j的計劃到站時間，為列車i在車站j的實際發車時間，是列車i在車站j的計劃發車時間。

1.2 約束條件

（1）列車區間運行時分約束

（2）停站時間約束

（3）列車追蹤間隔約束

其中，C為整條線路中列車的最小追蹤間隔。

（4）列車出發時間約束

該約束條件表示列車不得早于運行圖規定的時間發車。

2 改進粒子群算法

近年來，許多學者提出用智能算法來求解列車運行調整問題，主要采用遺傳算法（GA）和粒子群（PSO）算法等。根據PSO算法原理，設x{t}表示一個粒子（t為粒子個數），表示在第t個粒子中列車i在車站j的位置向量，為相應飛行速度，其值將會影響搜索最優解的效率，所以通常限定在一定范圍內，即Pbest表示在搜索最優解過程中的局部最優解，算法最后獲得的所有粒子中最優粒子的位置即調整后的列車運行時間，記為Gbest，則本文模型的PSO進化方程可以表示為：

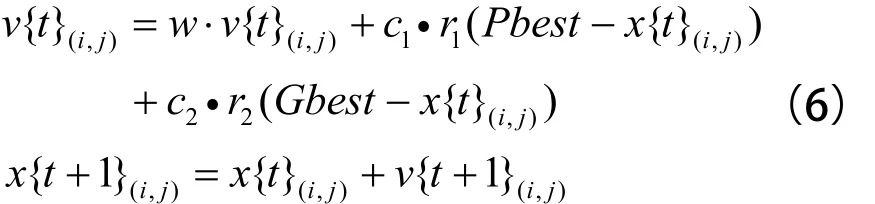
2.1 線性遞減權重

慣性權重w用于調節粒子對可行解的搜索能力。大量研究表明慣性權重w的取值被設定為0.9到0.4時，能使局部和全局得到平衡的開發及探索能力，所以將線性遞減權重w設置為迭代次數的函數[5]：

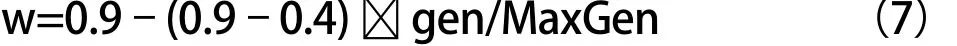
其中，gen為粒子當前迭代次數，MaxGen為粒子群總代數。

2.2 自適應速度限制

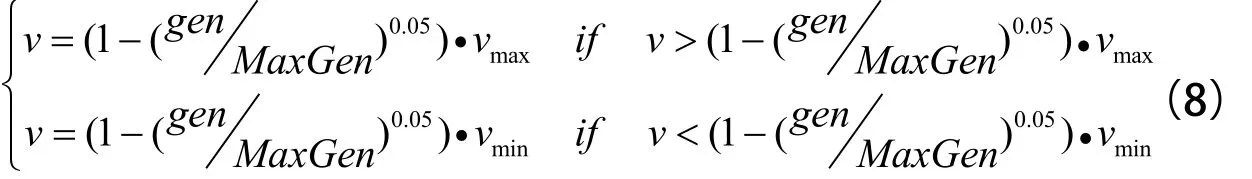
3 評價指標

為合理地對列車運行圖的晚點調整結果作出分析與對比，本文借鑒鐵路列車運行圖動態性能及其指標評價體系，建立相應的評價指標。這些評價指標既能通過仿真有關測試數據的結果計算出相應結果，也可更加直觀地反應出列車調整各個結果的優劣程度。

3.1 旅行時間延遲率

晚點傳播區段內所有晚點列車的晚點時間是模擬試驗中可以收集到的一項重要數據[7]，列車旅行時間延遲率α可以表述為仿真測試中列車晚點總傳播時間與圖定旅行時間T_travel之比，如式（9）所示。

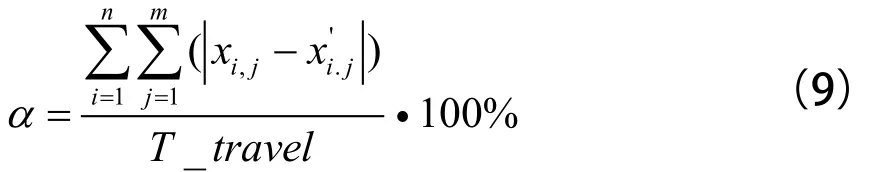
3.2 連帶晚點列車數

根據列車的實際運行情況和計劃運行圖的差異，設s為邏輯值，表示列車i在車站j是否發生晚點，則，設l為列車數，在晚點傳播區間內連帶晚點的列車數可表示為

3.3 晚點傳播區間

晚點傳播區間的大小描述了列車發生晚點后影響整個區段按圖行車的時間范圍[7]。以當前列車自身發生晚點的車站為起始點，其終點為晚點情況結束的車站，期間受到晚點影響的車站數即為晚點傳播區間的大小。

3.4 晚點時間擴散系數

根據晚點影響范圍，可以劃分為單列車晚點和列車群晚點[8]。單列車晚點的影響因素主要是列車本身和車站，列車群晚點中前行列車的晚點傳播對后續列車的影響較為明顯，可能出現正點到達、衰減、等值、增強傳播等情況。因此抑制晚點時間的擴散也就減小了晚點傳播對后續列車的影響，讓列車更快恢復到圖定計劃時刻。

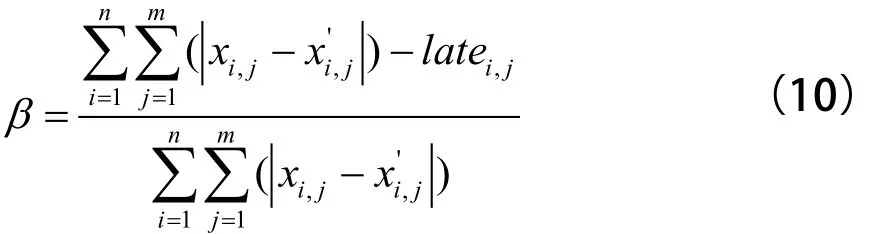
4 模型求解

4.1 停站時間模型求解

4.1.1 回歸模型及預測方法

回歸分析是由一個（或一組）普通變量來估計某一個隨機變量的觀測值所進行的統計分析，所求得的公式稱為回歸方程。本文采用回歸分析方法建立各車站平均客流量x與停站時間y的數學模型。在建立線性回歸模型時常用最小二乘法，即找出一條最佳的擬合曲線，使得這條曲線上的各點值與測量值誤差的平方和在所有的曲線中最小。而對于非線性回歸模型則需要轉化為線性回歸模型，然后再將求得的參數還原。

4.1.2 檢驗參數

本文對求出的停站時間模型必須進行參數檢驗，以此判斷該模型是否具有統計學意義及可行性。檢驗參數主要包括下面3個參數。

（1）R（相關系數）：反應停站時間y與各站平均客流量x之間具有線性關系的相對程度。當R值越接近于1，說明停站時間與平均客流量之間的線性關系就好。n表示客流量與停站時間對應的散點樣本數量。

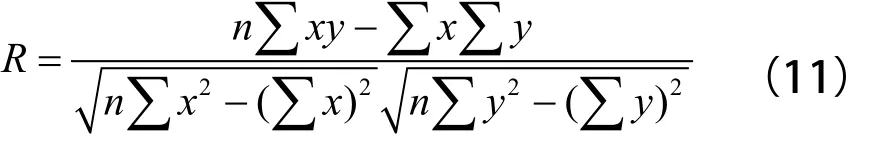
（2）R2（擬合優度）：回歸分析的決定系數。說明停站時間和平均客流量形成散點與回歸曲線的接近程度，R2∈ [0,1]。R2越大，回歸的越好，散點越集中于回歸線上。停站時間的理論預測值和真實的樣本值yi的距離越小，模型擬合度就越好。

（3）Sig值：回歸關系的顯著性系數。當Sig≤0.05時，說明回歸關系具有統計學意義；當Sig>0.05時，說明回歸關系沒有統計學意義，則模型不成立。

4.1.3 停站時間模型求解

根據成都地鐵1號線的車站客流和停站時間數據，采用回歸方法建立數學模型。首先得到每個車站的平均客流量和停站時間的若干對實測數據，將這些數據在坐標系中描繪出來，所得到的圖稱為散點圖。采用最小二乘法對該散點圖進行回歸分析，分別求出線性函數、二次項函數、三次項函數、指數函數的參數值，所得函數曲線繪制在圖1中。

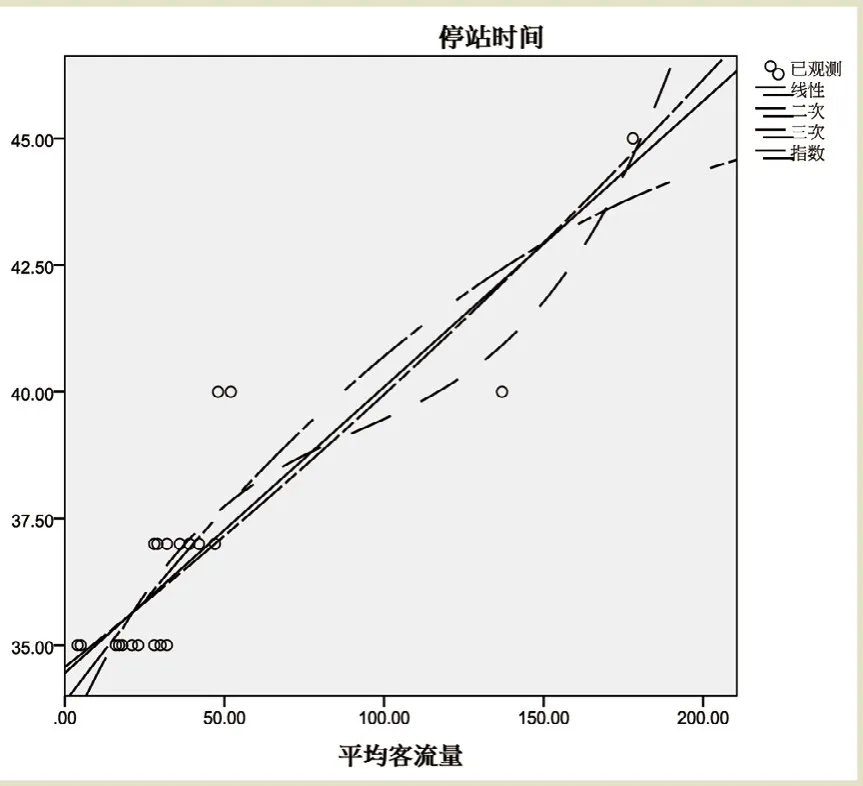
圖1 散點圖回歸分析

橫坐標表示各個車站的平均客流量，縱坐標表示停站時間，從圖1中看出用短虛線表示的3次項回歸函數與已觀測到的散點圖最接近。為了定量地說明各個回歸模型的擬合程度，求出其對應的評價指標，如表1所示。

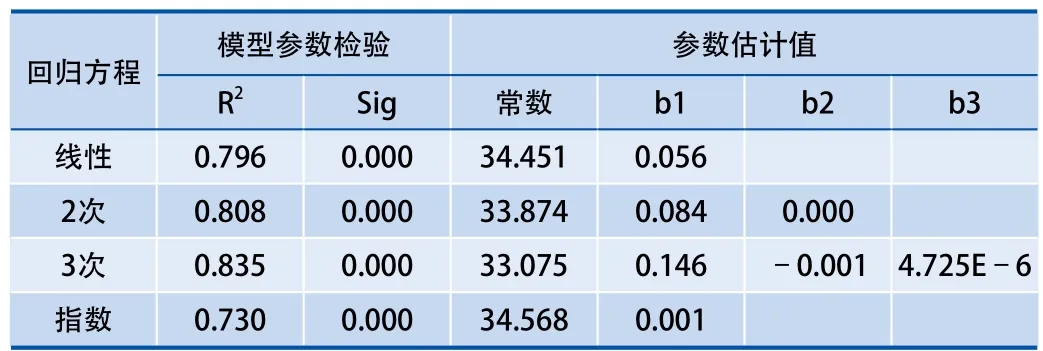
表1 回歸分析檢驗系數

參數估計值表示各個函數的參數值，表1中3次項函數的擬合程度較高R2=0.835，表示模型里83.5%的數據能達到良好擬合，變量t的檢驗顯著性Sig值小于0.05，表明各項參數都具有統計學意義，因此停站模型可以表示為：

4.2 仿真實例

案例采用成都地鐵的運行數據和MATLAB仿真平臺，對建立的調整模型結果進行驗證。車站數目14個，開行列數10列，列車圖定旅行時間為36 min 51 s。首先獲取列車的晚點信息，當采集到晚點信息后進行調整，最后輸出調整后的列車運行數據。

4.2.1 算法比較

假設列車10103在C站晚點150 s，分別采用遺傳算法（GA）、粒子群算法（PSO）和綜合改進粒子群算法（IPSO）進行調整并得到結果。

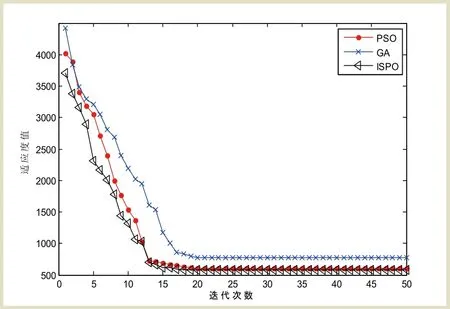
圖2 GA、PSO、IPSO的算法性能比較

圖2表示150 s晚點時GA、PSO、IPSO這3種算法的收斂曲線圖，橫坐標是算法的迭代次數，縱坐標表示目標函數值，在本優化模型中目標函數值代表實際運行圖與計劃運行圖的偏差，所以目標函數值越小越好。比較GA、PSO和IPSO算法得到的目標函數值，采用GA算法調整的結果較大，而PSO和IPSO兩種算法最后調整的結果基本一致，目標函數值隨著迭代次數的增加而逐漸減小，還發現，相比另外兩種算法，IPSO具有較好的收斂性。

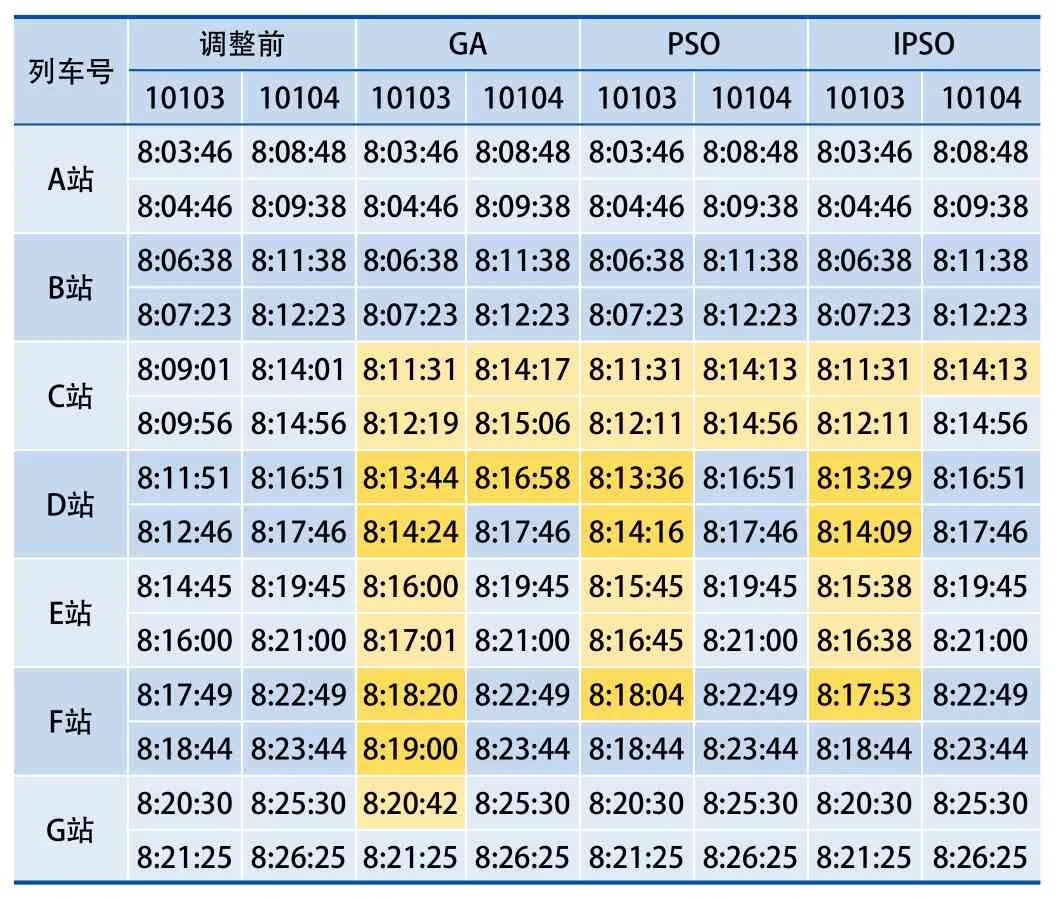
表2 算法調整前后的時刻表比較

表2列舉了10103列車晚點150 s時調整前的計劃運行時刻和采用GA、PSO、IPSO算法調整后列車在各車站的到達、出發時刻表。列車10103、10104次的晚點部分用黃色表示。

根據GA、PSO、IPSO這3種算法的調整結果，計算出相關評價指標對比，如表3所示。和表示10103次和10104次列車的旅行時間延誤率，β 表示列車晚點時間擴散系數，分別表示10103次和10104次列車的晚點傳播區間數。

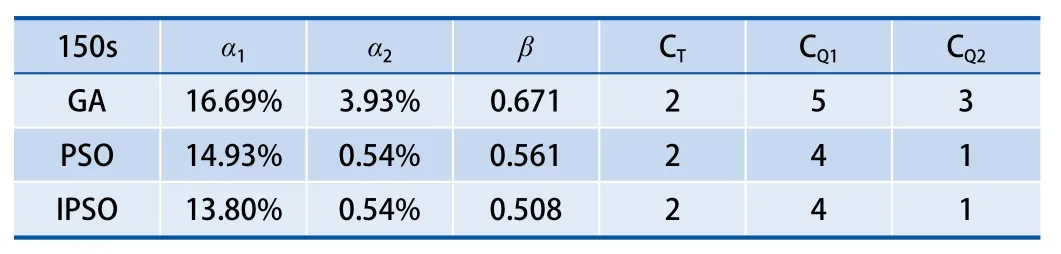
表3 3種算法的評價指標

4.2.2優化模型比較

根據上述分析，為驗證本文優化模型 ，采用IPSO算法對普通模型的目標函數和本文提出的基于客流量影響的優化模型分別進行調整并比較結果。假設10103次列車在C站晚點150 s，分別求解兩種模型下的調整結果，得到調整后列車出發、到達時刻表，部分結果展示如表4所示。

表4 普通模型和優化模型的時刻表

對比優化模型與普通模型的時刻表，兩者都能在較短時間內恢復正常行車秩序，主要差別體現在停站時間，如表5所示。

表5 停站時間比較

通過對時間數據的處理，表5定量地列出兩種模型調整結果的停站時間。普通模型是按照固定的停站時間運行，不隨當日交通客流量的變化而改變。但考慮客流量的停站時間模型加入目標函數后，停站時間發生改變。沒有發生晚點的車站繼續按計劃運行圖行車，發生晚點的各個車站，隨當日客流量的情況適當改變相應的停站時間，既滿足乘客出行的需要，也提高了城市軌道交通的運輸效率，使算法的調整結果更符合實際運輸情況。

5 結束語

城市軌道交通具有發車間隔小、車站間距短等特點，一旦發生列車延誤，很容易出現晚點傳播，影響后續列車的正常運行。本文考慮客流量的影響建立優化模型，引入帶懲罰函數的粒子群算法解決多約束、搜索范圍廣的列車運行調整問題。最后仿真驗證該模型的可行性，能使列車盡快恢復到計劃運行圖狀態，有效抑制晚點傳播的擴散。

[1]徐 蓓，郜春海，曹 芳.考慮乘客流影響的列車運行調整難點研究[J].鐵路計算機應用，2011，20（5）：1-4.

[2]賈傳峻，胡思繼，楊宇棟.列車運行調整微粒群算法研究[J].鐵道學報，2006，28（3）： 6-11.

[3]王宏剛，張 琦, 王建英， 等.基于遺傳算法的高速鐵路行車調整模型[J].中國鐵道科學，2006，27（3）：96-100.

[4]徐瑞華，江志彬，邵偉中，等.城市軌道交通列車運行延誤及其傳播特點的仿真研究[J]. 鐵道學報，2006，28（2）：7-10.

[5]賈勇兵．基干SVM的交通流短時預測方法研究[D].成都：西南交通大學，2009.

[6]Fan H. A modification to particle swarm optimization algorithm[J]. Engineering Computations, 2002，19（8）：970-989.

[7]楊肇夏，胡安洲.列車運行圖動態性能及其指標體系的研究[J].鐵道學報，1993，15（4）：46-56.

[8]金煒東，章優仕，高四維.列車運行調整的優化與仿真[J].科技導報, 2007，25（0712）： 18-22.

責任編輯 方 圓

Train operation adjustment of Urban Transit based on passenger fl ow inf l uence

CAO Jiru1, WANG Xiaomin1, CHEN Jianyi2
( 1.School of Information Science &Technology, Southwest Jiaotong University, Chengdu 610031, China; 2. Department of Communication and Signal, Guangzhou Railway(Group) Corporation , Guangzhou 510088, China )

Train operation adjustment was an important part of dispatching command of Urban Transit. It was diff i cult to obtain the satisfactory solution because of many constraints, larger search space and small range of feasible solution. According to the operation characteristics of Urban Transit, this article established train operation adjustment optimization model based on passenger fl ow inf l uence. The Improved Particle Swarm Algorithm was applied to solve the problem. Comparing with the Genetic Algorithm and Particle Swarm Algorithm, the model and the improved Algorithm were tested and verif i ed to be effective.

train operation adjustment; passenger; Particle Swarm Algorithm

U231.92∶TP39

A

1005-8451（2015）12-0013-05

2015-03-23

中國鐵路總公司科技研究開發計劃課題（2013X012-A-1，2013X012-A-2，2014X008-A），中央高校基本科研業務費專項資金(SWJTU11CX041)資助。

曹繼茹，在讀碩士研究生；王小敏，教授。