基于FAHP法的貧困生界定指標權重確定

姜濤

【摘要】以FAHP法為理論基礎，對貧困生界定的指標的權重進行構建。通過構建結構指標體系、確定指標體系權重的分步操作，達到定性分析與定量分析相結合， 找出提高貧困生界定效果的有效途徑。

【關鍵字】貧困生 權重 模糊矩陣 模糊層次分析法

一、前言

1999年以后，，我國的高等教育大幅度擴大高等教育招生規模。隨著教育規模的不斷擴大，申請困難資助的學生人數也越來越多， 在資助名額有限的情況下， 為使資助客觀、公平、公正地落實到真正困難學生身上， 做好貧困生的認定工作顯得尤為重要。傳統的認定方法主要靠自主申請和主觀判定， 缺陷是沒有嚴謹的理論指導， 難以保證甄別和判定的準確性[ 1] [ 2]。自學生資助工作實施以來， 我國高校投入了大量的精力用于貧困生的認定工作上， 但仍有很多局限性， 某項調查[ 3]表明， 僅有 57. 72%的學生認為認定后的貧困生與實際貧困學生情況完全相符或大體相當。

二、建立貧困生界定指標體系模型

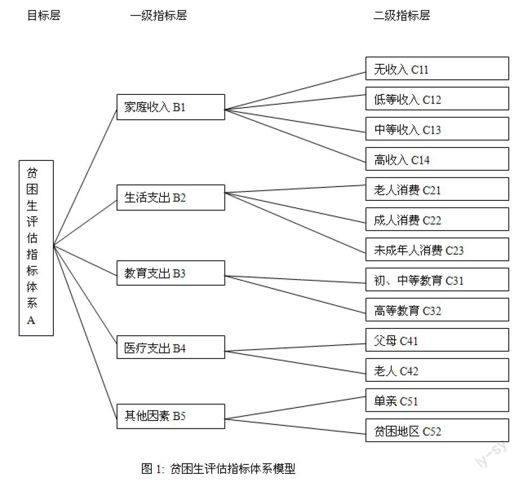
模糊層次分析法的模型建立與層次分析的模型建立相同。（見圖1）

圖1中的遞階層次結構共分為三層。第一層：目標層（A）；第二層：一級指標層（B1～B5） 是評價的主指標體系；第三層：二級指標層（C11～C14，C21～C23，C31～C32，C41～C42，C51～C52） 是對第二層指標的細化

三、確定指標體系權重

1、建立模糊一致判斷矩陣

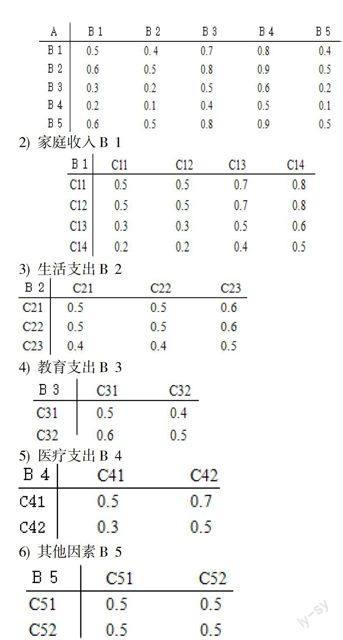
首先建立各層次的模糊矩陣：

1） 貧困生評價指標體系A

2、確定評價指標的權值

一級指標B1，…，B6對目標A的權重向量： ；

二級指標C11，…，C14對一級指標B1的權重向量： ；

二級指標C11，…，C14對目標A的權重向量：

二級指標C21，…，C23對一級指標B2的權重向量：

2、確定評價指標的權值

一級指標B1，…，B6對目標A的權重向量： ；

二級指標C11，…，C14對一級指標B1的權重向量： ；

二級指標C11，…，C14對目標A的權重向量：

二級指標C21，…，C23對一級指標B2的權重向量：