基于動態模糊神經網絡的并聯機器人魯棒復合控制研究

赫建立，朱龍英，成 磊，殷久誠

（1.常州大學 機械工程學院，常州 213164；2.鹽城工學院 汽車工程學院，鹽城 224051；3.西安工業大學 機械工程學院，西安 710021）

0 引言

并聯機器人具有結構穩定、運動負荷小、微動精度高、末端件慣性小以及快速的動態響應等優點，目前已被很多大型企業用于物品抓取、去毛刺、焊接等對零部件精度要求高的工作場合[1]。但作為被控對象，僅從其動力學觀點來分析，其剛體動力學模型是一個高度非線性且具有強耦合性的復雜系統，傳統的控制方法已無法對其軌跡跟蹤精度進行很好的控制。因此，并聯機器人系統的控制問題已成為目前急需解決的問題之一[2]。

由于6-DOF并聯機器人結構的復雜性，系統通常會存在參數攝動和外界不確定性因素的干擾問題，導致常規的設計方法已無法滿足控制系統的魯棒性與穩定性等要求。因此為了消除結構模型非線性和負載交聯耦合干擾對系統的影響，Kim等[3]設計了一種帶有摩擦估計器的魯棒非線性控制器并將其應用于6-DOF并聯機器人中，通過Alpha-beta跟蹤器獲得了系統的理想狀態。趙東亞等[4]對一種6-DOF并聯機構進行了非線性的分散魯棒控制器的設計，運用Lyapunov方法對系統的穩定性進行了分析，并結合SimMechanics仿真驗證了其有效性。朱大昌等[5]針對6-RPS型并聯機器人的模型誤差和負載交聯耦合干擾對系統的影響，提出了一種基于模糊神經網絡運算法則的自適應控制方法，設計了自適應控制器，并在控制系統中加入了模糊神經網絡運算法則，最后基于MATLAB軟件進行仿真實驗，實現了機器人軌跡跟蹤的高精度控制。文獻[6]針對并聯機構存在參數變動和模型誤差的情形時，提出一種基于模型的參考PID控制方法，基于Lyapunov函數方法優越的特點，設計了自適應控制器，實現了機構在做復雜運動時仍具有較高的跟蹤精度。楊擷泉等[7]針對一種液壓并聯機器人的桿件結構非對稱問題，提出了在輸入輸出信號中加入具有復合控制的模糊PID控制算法，并結合MATLAB軟件，采用仿真實驗證明了該方法不僅在很大程度上補償了并聯機器人系統非對稱的動力機構對運動系統產生的影響，而且提高了系統的抗干擾能力。

本文針對液壓伺服系統存在的參數攝動和復雜外干擾的問題，提出了一種基于動態模糊神經網絡的魯棒復合控制方法，并通過MATLAB仿真實驗驗證其性能。

1 并聯機器人的負載耦合分析

本文研究的6-DOF液壓并聯機器人的機構簡圖如圖1所示，六條分支桿件共同作用于同一個負載，從而出現了一系列交聯耦合干擾對系統軌跡跟蹤精度影響的問題。

假設忽略整個機構系統的摩擦力，則裝置于分支動桿上液壓缸的力平衡方程為：

式中，fi為第i條分支桿件液壓缸的實際輸出力矩；τi為第i條分支桿件液壓缸的液壓輸出力矩。

依據推導可以得到動平臺的動力學方程還可表示為：

其中，F=[FxFyFz]，M=[MxMyMz]

J-T可以表示為：

對式(1)、式(2)和式(3)分析可知：

公式(4)可以寫為：

其中，Y(s)為六條桿件的長度矩陣，且Y(s)=[y1y2…y6]T；Γ(s)為六條桿件的液壓輸出力矩矢量矩陣，Γ(s)=[ττ…τ]T。

126

H(s)為交聯耦合矩陣。

2 基于動態模糊神經網絡的魯棒復合控制器設計

為了使液壓系統具有更好的輸出性能，對控制系統進行了四種控制器的設計，PD控制器是為了使整個系統具有更好的魯棒性能；魯棒內回路控制器用來消除存在的參數攝動和外部復雜因素干擾；零相位誤差跟蹤控制器為了實現機構軌跡跟蹤的高精度控制；動態模糊神經網絡補償器為了實現對PD控制器的補償功能，并且為了進一步消除負載交聯耦合干擾對系統的影響，具體結構如圖2所示。

圖2 魯棒復合控制器框圖

2.1 魯棒內回路控制器的設計

為了消除存在的參數攝動和外部復雜因素干擾問題，對系統進行魯棒內回路控制器[8]的設計,結構框圖如圖3所示。其中K(s)代表反饋補償器；G(s)代表系統模型；Gn(s)代表名義模型。

圖3 魯棒內回路控制器

本文針對控制器K(s)的設計問題，提出了對系統加入一種濾波器Q(s)，并加入H∞混合靈敏度的優化方法。

本文選擇的濾波器Q(s)為：

圖4 干擾觀測器框圖

如果將Q(s)替代K(s)，則可以用圖4來等價的表示圖3的結構模型，只要能夠使式(6)成立，則控制器就可以轉化為干擾觀測器的結構，然后基于此干擾觀測器的基礎上對系統進行分析。

將ur，d，ξ作為輸入，則根據疊加原理可以推導出系統的輸出為：

并且有：

假設Q(s)為理想的濾波器，設Q的頻帶為fq，當當處在低頻段時Q(s)=1，且有：

當處在高頻段時f≥fq，Q(s)=0且有：

通過上述分析可知，在對Q(s)優化并處于低頻段時Q(s)≈1，針對各種參數攝動和復雜外部干擾具有較強的抑制作用，且提高了系統的魯棒性。

干擾觀測器的傳輸函數Gol(s)，靈敏度函數SQ以及補靈敏度函數TO分別為：

本文基于H∞混合靈敏度[9]的優化方法對Q(s)進行設計。而且求出了最優控制器K(s)。可以將H∞表示為：

其中，W1、W2代表權值系數。

以下將基于H∞理論法設計系統的最優控制器K(s)。

根據對液壓伺服系統的分析可以得到其名義模型為：

其中W1、W2取值為：

基于MATLAB環境下的Robust工具箱，并依據式(20)得到了系統的最優魯棒內回路控制器為：

2.2 位置閉環控制器的設計

本文針對系統采用PD控制，以提高系統的穩定性能，并設置其控制器的關鍵參數為Kp=5.9，Kd=0.031。

2.3 零相位誤差跟蹤控制器的設計

本文提出一種零相位誤差跟蹤控制器用于實現動平臺軌跡跟蹤的高精度控制[10]。

系統的離散事件傳遞函數為：

其中，z-d表示模型的延遲導致的滯后，d表示延遲步數。

系統的零點、極點可由如下公式得到：

引入逆系統作為其前饋控制器，則:

對于式(25)所描述的系統，如果輸入信號中的d+n值已知，那么控制器可以表示為：

以下對系統的零相位誤差跟蹤控制器進行設計然后將輸入信號設置為正弦函數，并且測量處于不同頻率下的相位差，傳遞函數為：

將Gc(s)離散化可得：

G(z-1)含有一個不穩定點z=9.1410，所以依據原理

cu可以獲知ZPETC為：

2.4 動態模糊神經網絡補償器的設計

動態模糊神經網絡[11]如圖5所示，用xn作為網絡的第n個輸入，作為第k個節點的凈輸入。

圖5 四層動態模糊神經網絡結構

第一層：輸入層。本文針對輸入信號作如下的歸一化處理：

i的最大值。

第二層：隸屬函數層。

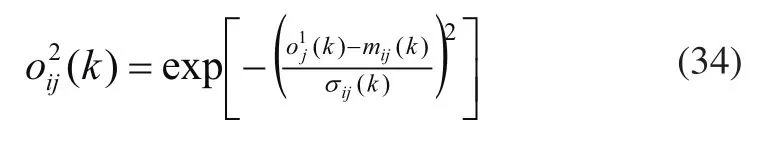
式中，mij代表第i個輸入量的第j個模糊語言變量隸屬函數的均值；σij代表第i個輸入量的第j個模糊語言變量隸屬函數的標準值。

第三層：模糊規則層。

第四層：輸出層。主要用于去模糊操作。

式中，wij為權系數；n1表示x1的模糊變量個數；n2表示x2的模糊變量個數。

將模糊網絡的參數用矩陣等形式體現出來，可知輸入為：

輸出為:

輸入隸屬函數的向量可表示為：

回歸權向量為：

輸出權向量為：

根據上述的分析可知，動態模糊神經網絡的輸出可表示為：

液壓系統模型為三階系統，經簡化后的方程為：

可以推出魯棒復合控制器的輸出為：

將式(46)帶入式(45)可得：

根據式(47)可知：

定義變量：

由式(48)和式(49)可知：

綜上分析，當λ=0時，動態模糊神經網絡對外部復雜干擾進行了完全的補償。

取性能指標函數為:

根據梯度下降法可得神經網絡的迭代算法為：

根據式(44)可得：

在對魯棒復合控制器進行設計時，可以取其輸入變量分別為e和uf，它們分別都取五個模糊變量，并且可得e和uf的初始參數為：

經推導可以得到模糊神經網絡有25條模糊規則，設規則層與輸出層之間的初始參數W為：

當基于動態模糊神經網絡補償器對系統進行控制時，液壓系統的模型參數為：

3 仿真實驗研究

本文將基于MATLAB軟件對6-DOF并聯機器人的單通道液壓系統展開深入的仿真實驗研究。

文章中PD表示閉環控制器，RIC表示魯棒內回路控制器，ZPETC表示零相位誤差跟蹤控制器，DFNN表示動態模糊神經網絡補償器。

仿真參數設置如下：桿長幅值0.01m，采用正弦信號，頻率為0.5Hz，液壓系統單通道受到的干擾力是設置液壓無阻尼頻率為ωh和液壓阻尼比ξh是可以變動的，假設：

當基于PD控制時，得到如圖6所示的仿真圖形；當加入本文提出的PD+RIC+ZPETC+ZPETC魯棒復合控制器時，得到如圖7所示的仿真圖形。

依據圖6分析可知，當系統采用PD控制時，軌跡跟蹤誤差大約為[-0.0005,0.002]，反映出嚴重的不對稱性，原因主要是系統負載交聯耦合干擾對系統的影響，當基于PD+RIC+ZPETC+ZPETC控制時系統的誤差保持在[-0.0002,0.00025]，由此可知，魯棒復合控制器的應用大大的消除了系統參數攝動和外部復雜因素干擾的問題，在很大程度上提高了液壓系統的運動性能。

圖6 PD控制跟蹤曲線

圖7 PD+RIC+ZPETC+ZPETC控制跟蹤曲線

4 結束語

本文提出的基于動態模糊神經網絡的并聯機器人魯棒復合控制方法，解決了并聯機器人液壓伺服系統存在的參數攝動和外界不確定性因素干擾的問題，文章分別通過PD控制和基于動態模糊神經補償器的魯棒復合控制對系統的運動性能進行了仿真分析，結果證明，本文提出的魯棒復合控制方法在性能上遠遠優于傳統的PD控制，值得推廣使用。

[1]成磊,朱龍英,鄭帥,等.并聯機器人的粒子群優化神經網絡自適應控制算法研究[J].制造業自動化,2014,36(6):5-7.

[2]朱大昌,劉運鴻,馮文結.3-RPC型并聯機器人模糊PID控制系統研究[J].機械傳動,2014,38(002):114-117.

[3]Kim H S,Cho Y M, Lee K.Robust nonlinear task space control for 6 DOF Parallel manipulator[J].Automatica,2005,41(9):1591-1600.

[4]趙東亞,李少遠,高峰.六自由度并聯機器人分散魯棒非線性控制[J].控制理論與應用,2008,25(5):867-872.

[5]朱大昌,陳強.基于模糊神經網絡運算法則的并聯機器人自適應控制研究[J].控制理論與應用,2010,29(1):4-7.

[6]魯開講,師俊平,淡卜綢.基于穩定性的并聯機構自適應控制[J].農業機械學報,2012,43(1):202-207.

[7]楊擷泉,趙克定,吳盛林.液壓六自由度并聯機器人控制策略的研究[J].機器人,2004,26(3):263-266.

[8]Bong K, Choi h.Analysis and design or robust motion controllers in the unified frameworks[J].Journal of Dynamic System,Measurement and Control,2002,124(6):313-321.

[9]方強,姚郁.電動負載模擬器擾動觀測器系統化設計[J].哈爾濱工業大學學報,2007,39(3):349-353.

[10]Tomizuka M, Zero phase error tracking algorithm for digital control[J].ASME Journal of Dynamic Systems Measurement and Control,1987,109(1):65-68.

[11]Chen Y C,Teng C C.A model reference control structure using a fuzzy neural network[J].Fuzzy Sets and Systems,1995,73(2):291-312.