電磁場中電勢的辨析

丁蕾

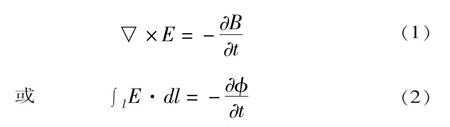
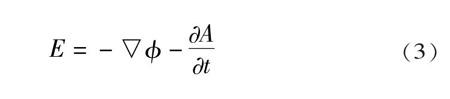
摘要：場是物理學科教學中電磁學部分的重要概念，而勢是場量求解過程中常用到的“輔助”物理量。在職業學校的物理教學中，學生熟悉的都是靜電場，對既有縱場也有橫場的情況感到難以理解。所以對電動勢和電勢這兩個常見的概念進行辨析，將有助于學生強化電磁場的概念。

關鍵詞：電磁場;電動勢;電勢

中圖分類號：G712 文獻標志碼：A 文章編號：1673-9094-（2015）12C-0025-03

電場強度E與磁感應強度B是求解電磁場的最終目標，但在求解的過程中，往往會根據具體情況引入標勢或矢勢。在職業學校的物理教學中，一般只涉及在靜電場的情況下引入電標勢，簡稱為電勢。但是教材同時也要求學生了解變化的磁場產生的渦旋電場。雖然對于電磁感應，教學重點內容是磁通量，但是從理解電磁場本質的角度來看，即理解麥克斯韋的電磁理論[1]：變化的磁場產生電場，變化的電場產生磁場，還是很有必要對靜電場與渦旋電場同時存在時的勢進行討論。

對于靜電場與渦旋場同時存在時是否可以使用電勢這個概念問題，目前有兩種觀點。[2]其一是電勢是無旋有源的靜電場中的概念，它不能被“引申”到無源有旋的渦旋場中去。其二是可以引進電勢的概念。因為在環路中存在電流時，從全電路來看電場的安培環路定理依然成立，所以可以使用電勢的概念。為了準確回答這個問題，我們必須先要厘清相關概念。

一、靜電場和感生電場的區別與聯系

從這兩種電場的產生來分析，靜電場中電荷密度不隨時間變化而變化，所以在理論上討論靜電場時都是分析相對于觀察者靜止的電荷產生的場。故而靜電場往往又稱為庫侖場，它與磁場的存在沒有必然的關系。在實驗中，描繪靜電場的等勢面或線時，往往用穩恒電流場來模擬靜電場。比如在平面上將直流電的正極設置在圓平面的圓心處，負極設置為以R為半徑的環形電極，如此等勢面便為以正極為圓心的一系列同心圓。雖然等勢面與處于圓心處的靜止電荷產生的場一致，但不同的是此時必定存在穩恒的磁場。

渦旋電場是由變化的磁場產生的，它的強弱由磁場隨時間的變化率決定。即

（1）

或（2）

從電與磁的對稱角度來看，變化的磁場能產生電場，變化的電場必定能對產生磁場做出貢獻。在高中階段一般只介紹穩恒電流產生的磁場，其實電場變化產生的磁場即是通過引入麥克思韋位移電流來體現的。雖然不必要求學生了解麥克思韋位移電流與磁場強度之間的定量關系，但是這種電與磁的對稱關系是有必要了解的，因為它涉及我們常說的物理圖像或物理思想。

從它們對放入其中的電荷的作用來分析，不論是靜電場還是渦旋場，放入的電荷都會受到電場力的作用，力的大小與電荷的量與場強都成正比，且正電荷受力的方向與場強方向一致。但通常將靜電場對電荷的作用稱為靜電力，而將渦旋電場對電荷的作用力歸屬為非靜電力的一種。在靜電場中沿任意一個回路移動電荷，電場力做功為零，且在靜電場中任意兩點間移動電荷，電場力做功與移動的路徑無關，只與電荷在電場中的初末位置有關，即電荷在場中的能量只與電荷在電場中的位置有關。與重力場相似，靜電場是有源無旋的保守力場，故可以引入電勢的概念來描述靜電場的各種性質。而渦旋電場的電場線是閉合的，它是無源有旋場。在渦旋電場中，電荷沿閉合回路移動一圈，渦旋電場對電荷做的功不為零，所以渦旋電場對電荷的作用力不是保守力，引入電標勢的概念是不適合的。事實上，在電磁學理論中，對于這種情況是用電標勢與磁矢勢一起來表達電場強度的，即

（3）

二、電路分析中的電動勢與電勢

上文用電磁場來分析和理解電勢，但是教材的習題或試題多是以電路的形式出現。雖然我們知道用電磁場的方法來分析電路與傳統的宏觀電路分析方法本質上是一致的，特別是在處理主頻電路時，必須使用場的分析方法，但在職業學校的物理教學中，學生還無法達到這一認識層次，所以電動勢的概念顯得尤為重要。

教材中明確指出：把單位正電荷從負極通過電源內部移到正極時，非靜電力所做的功，就是電源的電動勢。而感生電動勢是由非靜電力移動電荷做功而產生的，這里的非靜電力就是電荷在渦旋電場中受到的電場力。因為當我們討論確定的電路時，即是已經知道了確切的路徑，所以在分析電路時，如果存在渦旋場，則在電路中應等價引入一個或多個“電源”。這樣感生電動勢或電源是在導體中維持某種電荷（或電流）分布的必要條件，可以看作是電路的電源部分，因而在外電路中，電勢、電勢差和電壓等與沒有渦旋場存在時便一致，分析電路中的電勢高低或差值便可以應用含源的歐姆定律了。

三、涉及渦旋場的高考題分析

如上所分析的存在渦旋電場的電路問題，通常考察感應電動勢大小、電場中任一點的場強大小，以及渦旋電場做功的多少。這三類問題都可以用（2）式來進行分析。求感應電動勢大小的試題，對（2）式中環路積分可以用微元法，由于高中階段的學生沒有學過積分，所以需要定量計算的試題通常給出的是環狀回路。因為渦旋電場的方向與環路的切線方向總是一致的，所以（2）式左邊即是渦旋電場強度E乘以環路的周長，而利用（2）式右邊磁通量的變化率可求電動勢大小，然后除以環路的長度即可得到場強。

如2012年福建高考理科綜合試題[3][4]，這道試題的重點就在如何求出電場強度來。通過磁感應強度隨時間變化的關系圖可以看出，磁感應強度只是在一段時間內線性增加。在這一段時間內，環形導軌中存在渦旋電場，利用（2）式就可以計算得其大小。而渦旋場做功的大小可以用功能原理，也可以用電場力做功的公式求出，但此時考察的重點已經發生了變化。

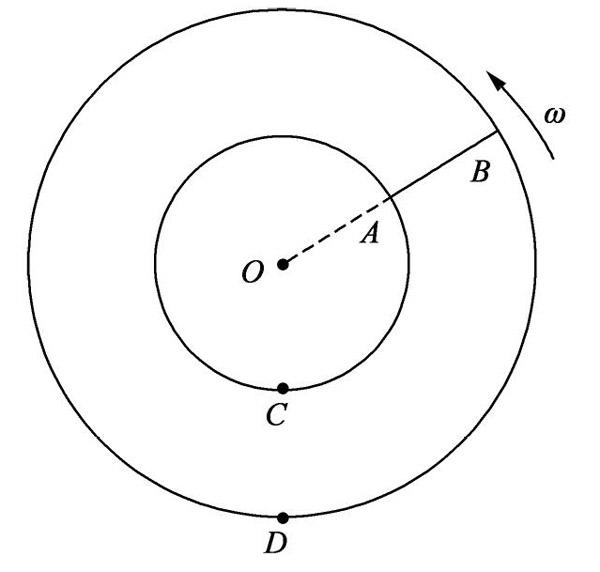
再如2011年浙江物理高考題，也是給出了磁感應強度隨著時間變化的關系圖，可以根據其線性變化關系，用（2）式求出感應電動勢的大小。但值得注意的是，（2）式雖然可以由（1）式兩邊取面積分推得，但（2）式在使用的時候，右邊的磁通量變化率未必是磁感應強暴隨時間變化而產生的。如新課標2014年的高考題：半徑分別為r和2r的同心圓形導軌固定在同一水平面內，一長為r、質量為m且質量分布均勻的直導體棒AB置于圓導軌上面，BA的延長線通過圓導軌中心O，裝置的俯視圖如圖所示。整個裝置位于一勻強磁場中，磁感應強度的大小為B，方向豎直向下。在內圓導軌的C點和外圓導軌的D點之間接有一阻值為R的電阻（圖中未畫出）。直導體棒在水平外力作用下以角速度ω繞O逆時針勻速轉動，在轉動過程中始終與導軌保持良好接觸。高導體棒與導軌之間的動摩擦因數為μ，導體棒和導軌的電阻均可忽略。策略加速度大小g。求通過電阻R的感應電流的方向和大小;外力的功率。

此題在求解過程中必須求出電動勢的大小，但此時顯然是動生電動勢，因為磁感應強度B并不隨時間變化。但磁通量卻是一直在變化，故而AB與CD間的阻，以及導軌構成的回路面積在隨時間變化，所以仍然可以使用（2）式進行求解。

綜上所述，涉及非靜電場時，電標勢的概念只對庫侖場有意義，而對渦旋場是沒有意義的。在討論電路問題時，將感應電動勢看作是電路中的電源，便可以應用含源電路的歐姆定律，如靜電場問題一樣來討論電勢、電勢差和電壓了。

參考文獻：

[1]郭碩鴻.電動力學[M].北京：高等教育出版社，2008.

[2]沈志斌.關于渦旋電場的電勢問題[J].物理教師，1990（4）.

[3]徐慧.談談2012年高考中渦旋電場問題[J].中學物理，2013（31）.

[4]王添華.渦旋電場中電勢高低如何判斷[J].物理教師，2014（35）.

（責任編輯：馮志軍）

Discrimination of Electric Potential in Electromagnetic Field

DING Lei

（Xuzhou Education Bureau， Xuzhou 221000， Jiangsu Province）

Abstract： Field is an important concept in electromagnetics in Physics teaching， while potential is commonly used in field solving process as an auxiliary physical quantity. In the Physics teaching in vocational schools， the students are familiar with the electrostatic field， but they have difficulty in understanding the situation with both longitudinal field and the transverse field. Therefore， the discrimination of electromotive force and electric potential will help to strengthen the students' understanding of the electromagnetic field.

Key words： ?electromagnetic field; electromotive force; electric potential