美國(guó)海軍陸戰(zhàn)隊(duì)傷病員醫(yī)療后送分析及啟示
齊亮,劉曉榮
自2017 年11 月美國(guó)參謀長(zhǎng)聯(lián)席會(huì)議發(fā)布JP4?02 聯(lián)合出版物《聯(lián)合衛(wèi)勤》條令(簡(jiǎn)稱(chēng)“條令”)至今,美海軍陸戰(zhàn)隊(duì)的衛(wèi)勤保障出現(xiàn)了諸多變化,反映出其衛(wèi)勤行動(dòng)理念和實(shí)踐,尤其是海軍陸戰(zhàn)隊(duì)醫(yī)療后送發(fā)展的新趨勢(shì)。現(xiàn)分析如下,并總結(jié)提出對(duì)我國(guó)海軍陸戰(zhàn)隊(duì)衛(wèi)勤改革的啟示與建議。
1 海軍陸戰(zhàn)隊(duì)在傷病員管理層級(jí)上的特殊性
條令中提出了4 個(gè)傷病員管理層級(jí)。美軍在使用“ca?sualty”時(shí),常暗含著衛(wèi)生減員的含義[1],因此傷病員管理層級(jí)所要救護(hù)的不僅包括傷員,而且包括病員。根據(jù)職責(zé)的不同,醫(yī)療救護(hù)人員被定義為不同的層級(jí),所有執(zhí)行野戰(zhàn)任務(wù)的部隊(duì)在遭受傷病后都會(huì)得到對(duì)應(yīng)層級(jí)的救護(hù),海軍陸戰(zhàn)隊(duì)也不例外。
第一級(jí)是第一反應(yīng)者救護(hù)(first responder care,F(xiàn)RC)層級(jí)(層級(jí)1)。FRC 是指由第一時(shí)間為傷病員提供急救措施的單位或個(gè)人所實(shí)施的救護(hù)工作,既包含了自救互救,也包含了由戰(zhàn)斗救生員、海軍看護(hù)兵等醫(yī)療相關(guān)人員實(shí)施的救治。如果實(shí)施救治的專(zhuān)業(yè)醫(yī)療人員能夠判定傷病員所患為常規(guī)疾病,并能給予簡(jiǎn)單治療,或能夠及時(shí)處置,在治療和處置后可要求傷病員即刻歸隊(duì)。對(duì)于必須執(zhí)行后送的傷病員,只能由專(zhuān)業(yè)醫(yī)療人員實(shí)施傷病員的集中處置,然后提出后送需求。美軍對(duì)所有需要為海軍陸戰(zhàn)隊(duì)傷病員實(shí)施救治的專(zhuān)業(yè)醫(yī)療人員都提出了比普通陸軍軍醫(yī)更高的要求:如果尚未具有專(zhuān)業(yè)醫(yī)師資格,醫(yī)療人員必須在執(zhí)行任務(wù)前完成強(qiáng)化醫(yī)療訓(xùn)練課程。
第二級(jí)是前沿復(fù)蘇救護(hù)層級(jí)(層級(jí)2)。其醫(yī)療人員任務(wù)是完成包含層級(jí)1 職責(zé)在內(nèi)的高級(jí)創(chuàng)傷管理和緊急醫(yī)療處置工作,要能在層級(jí)1 職責(zé)的基礎(chǔ)上,提供更高水平的傷病員復(fù)蘇,且至少能夠完成損傷控制手術(shù)。另外,在條件允許的情況下,他們也可以完成有限的輸血、輸液、影像診斷以及戰(zhàn)斗壓力控制工作。層級(jí)2 又可進(jìn)一步分為初級(jí)(light maneuver,LM)和高級(jí)(enhanced,E)這2 種類(lèi)型。層級(jí)2 初級(jí)人員的職責(zé)包含了將術(shù)后傷病員后送至層級(jí)3 處進(jìn)行救護(hù)的相關(guān)工作;而層級(jí)2 高級(jí)人員的職責(zé)中則又額外增加了在重癥加強(qiáng)護(hù)理病房?jī)?nèi)救治傷病員的工作,他們不僅要具備為傷病員開(kāi)展第一次手術(shù)的能力,而且要負(fù)責(zé)將術(shù)后的傷病員后送至層級(jí)4 處進(jìn)行救護(hù)。值得注意的是,對(duì)海軍陸戰(zhàn)隊(duì)傷病員實(shí)施救護(hù)的人員中沒(méi)有層級(jí)2 初級(jí)人員。也就是說(shuō),一旦發(fā)生傷病員,F(xiàn)RC 除了層級(jí)1 外,就只能依靠層級(jí)2 高級(jí)人員。按照美軍的相關(guān)規(guī)定,如果承擔(dān)高級(jí)人員職責(zé)的層級(jí)2 不是單獨(dú)的一個(gè)人而是一級(jí)救治機(jī)構(gòu),在該層級(jí)完成了對(duì)海軍陸戰(zhàn)隊(duì)傷病員的救治之后,傷病員可以無(wú)須通過(guò)層級(jí)3,直接被后送至層級(jí)4 處,實(shí)施越級(jí)后送。
第三級(jí)是戰(zhàn)區(qū)醫(yī)院治療層級(jí)(層級(jí)3)。該層級(jí)通常是能收治所有類(lèi)型傷病員的一級(jí)救治機(jī)構(gòu),如同一所完整的醫(yī)院,有足夠的資源實(shí)施復(fù)蘇、外科手術(shù),完成術(shù)后治療。這是對(duì)層級(jí)2 的一種拓展,不能經(jīng)受長(zhǎng)途后送的傷病員,可以被送往這一級(jí)機(jī)構(gòu)進(jìn)行手術(shù)。層級(jí)3 一般由野戰(zhàn)醫(yī)院承擔(dān),其工作職責(zé)中不包含醫(yī)療后送工作。海軍陸戰(zhàn)隊(duì)的醫(yī)療后送鏈中并沒(méi)有此層級(jí)。
第四級(jí)是確定性救護(hù)層級(jí)(層級(jí)4)。執(zhí)行者是位于美國(guó)本土的醫(yī)院,以及美軍海外基地內(nèi)的救治機(jī)構(gòu)。其通常作為醫(yī)療后送鏈的末端,如果沒(méi)有特殊情況,傷病員不會(huì)被繼續(xù)后送,而是在這類(lèi)機(jī)構(gòu)中完成全部治療。對(duì)海軍陸戰(zhàn)隊(duì)的傷病員而言,完成其確定性治療的機(jī)構(gòu)可以不是海軍陸戰(zhàn)隊(duì)或海軍的醫(yī)療機(jī)構(gòu)。只要實(shí)施后送的需求是由層級(jí)2 高級(jí)人員提出的,海軍陸戰(zhàn)隊(duì)的傷病員就有可能被安排到任何一家可以承擔(dān)層級(jí)4 的醫(yī)療機(jī)構(gòu)。
2 海軍陸戰(zhàn)隊(duì)的傷病員后送鏈
既往以陸軍為主體保障對(duì)象的醫(yī)療后送(medical evacu?ation,MEDEVAC)概念,在美軍軍語(yǔ)中是指利用專(zhuān)業(yè)后送平臺(tái)將傷病員從受傷地點(diǎn)送往醫(yī)療機(jī)構(gòu)或在兩級(jí)醫(yī)療機(jī)構(gòu)之間實(shí)施的后送活動(dòng),以及在途中于專(zhuān)業(yè)后送平臺(tái)上實(shí)施的救治活動(dòng)。而由非專(zhuān)業(yè)平臺(tái)執(zhí)行的活動(dòng),常被稱(chēng)為傷病員后送(casualty evacuation,CASEVAC)。以上2 個(gè)概念與我軍的醫(yī)療后送概念存在很大差異[2],都不屬于醫(yī)療救治的范疇。在《聯(lián)合衛(wèi)勤》中,美軍使用了一個(gè)更加直觀的概念。他們將傷病員單純?cè)诳臻g中的位置變化統(tǒng)稱(chēng)為患者移動(dòng),用于統(tǒng)一表示傷病員在醫(yī)療后送鏈中的轉(zhuǎn)運(yùn)過(guò)程。完成患者移動(dòng)的工作,既可以是規(guī)范化的專(zhuān)業(yè)MEDEVAC,也可以是單純的CASEVAC,同時(shí)還包括了空運(yùn)醫(yī)療后送(aeromedical evacua?tion,AE)。雖然專(zhuān)業(yè)的途中醫(yī)療救護(hù)不是必須的,但在資源允許且傷病員有切實(shí)需求的情況下,應(yīng)當(dāng)盡可能地提供MEDEVAC 而非CASEVAC。
圖1 顯示了美海軍陸戰(zhàn)隊(duì)完整的傷病員后送路徑。處于起點(diǎn)位置的是自救互救,用于完成FRC 層級(jí)1 的大部分工作。雖然每支海軍陸戰(zhàn)隊(duì)中都至少有一名學(xué)過(guò)基礎(chǔ)急救課程、接受過(guò)創(chuàng)傷救護(hù)訓(xùn)練的戰(zhàn)斗救生員,但他不屬于專(zhuān)業(yè)醫(yī)療人員,只相當(dāng)于我軍衛(wèi)生戰(zhàn)士的角色,所以,海軍陸戰(zhàn)隊(duì)傷病員的自救互救工作通常沒(méi)有專(zhuān)業(yè)醫(yī)療人員的介入。戰(zhàn)斗救生員只能負(fù)責(zé)在專(zhuān)業(yè)醫(yī)療人員到達(dá)之前提供強(qiáng)化急救措施,但沒(méi)有提出后送需求的權(quán)力。美國(guó)海軍陸戰(zhàn)隊(duì)在戰(zhàn)時(shí)往往采取戰(zhàn)斗編組形式,由地面戰(zhàn)斗單元、航空戰(zhàn)斗單元和后勤戰(zhàn)斗單元規(guī)模不等的陸空特遣部隊(duì)參與作戰(zhàn)。如果地面戰(zhàn)斗單元中的一線部隊(duì)可以得到航空戰(zhàn)斗單元下屬航空聯(lián)隊(duì)的支持,聯(lián)隊(duì)中的支援中隊(duì)衛(wèi)勤人員也可以擔(dān)負(fù)起層級(jí)1 的職責(zé)。完成自救互救的傷病員在被送往專(zhuān)業(yè)救治隊(duì)伍之前,絕大多數(shù)都會(huì)得到海軍看護(hù)兵的救護(hù)。看護(hù)兵相當(dāng)于我軍的衛(wèi)生員,編制在醫(yī)療排中的看護(hù)兵,戰(zhàn)時(shí)會(huì)被分配到每個(gè)戰(zhàn)斗隊(duì)伍之中,承接自救互救之后的救護(hù)工作。在前線為海軍陸戰(zhàn)隊(duì)隊(duì)員提供救護(hù)的相關(guān)人員也可能來(lái)自營(yíng)/連救護(hù)站。如果一線戰(zhàn)斗隊(duì)伍沒(méi)有配備衛(wèi)生力量,則團(tuán)一級(jí)的衛(wèi)生力量可以前出進(jìn)行保障。
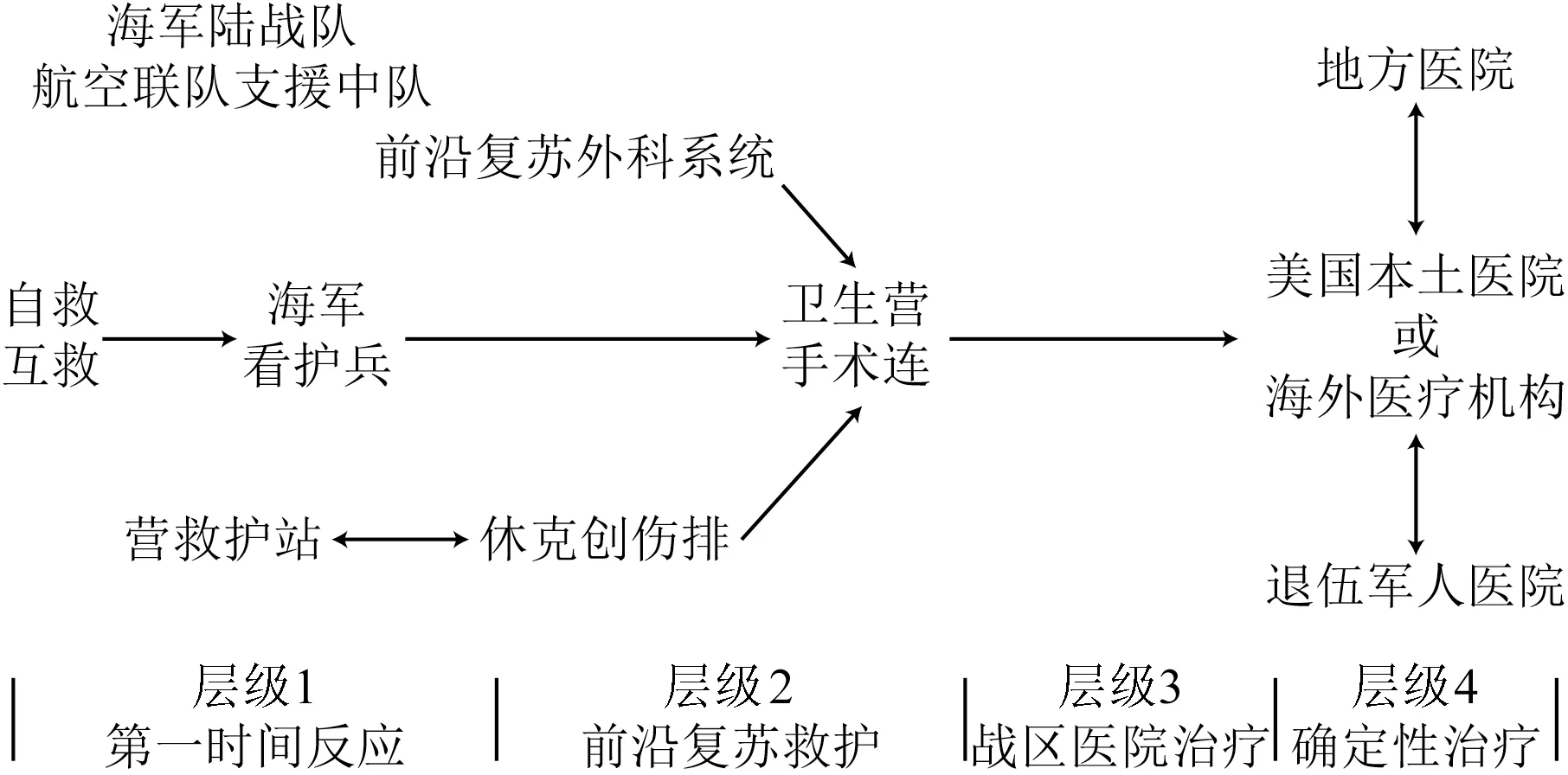
圖1 美海軍陸戰(zhàn)隊(duì)傷病員后送鏈
可以為海軍陸戰(zhàn)隊(duì)傷病員執(zhí)行層級(jí)2 高級(jí)人員職責(zé)的單元較多,包括前沿復(fù)蘇外科系統(tǒng)、休克創(chuàng)傷排以及衛(wèi)生營(yíng)、手術(shù)連等專(zhuān)業(yè)醫(yī)療隊(duì)伍。與美國(guó)陸軍的前沿外科手術(shù)隊(duì)相似,美國(guó)海軍陸戰(zhàn)隊(duì)的前沿復(fù)蘇外科系統(tǒng)(forward resuscita?tive surgery system,F(xiàn)RSS)是可以獨(dú)立開(kāi)展手術(shù)的最小單元,其最多可以承擔(dān)18 名傷病員的全類(lèi)型創(chuàng)傷救護(hù)任務(wù),包括傷病員分類(lèi)、高級(jí)創(chuàng)傷生命支持等,是海軍陸戰(zhàn)隊(duì)在登陸作戰(zhàn)一線實(shí)施復(fù)蘇治療的主要力量。FRSS 留置傷病員的時(shí)間不能超過(guò)4 h,一旦條件允許,就應(yīng)當(dāng)盡快實(shí)施MEDEVAC。休克創(chuàng)傷排(shock trauma platoon,STP)是為陸空特遣部隊(duì)中除后勤戰(zhàn)斗單元外其他戰(zhàn)斗單元的傷病員提供直接保障的專(zhuān)業(yè)醫(yī)療隊(duì)伍,其可以根據(jù)衛(wèi)勤預(yù)案進(jìn)行提前部署,幫助營(yíng)救護(hù)站減輕救護(hù)壓力,接收經(jīng)營(yíng)救護(hù)站處置過(guò)的傷病員,使其有機(jī)會(huì)更加靠近一線部隊(duì)。STP 有時(shí)也會(huì)被部署到前沿復(fù)蘇外科系統(tǒng)附近,為其提供傷病員的術(shù)前或術(shù)后救護(hù)。與上述2 種更具有機(jī)動(dòng)衛(wèi)勤力量屬性的專(zhuān)業(yè)醫(yī)療隊(duì)伍不同,衛(wèi)生營(yíng)是美國(guó)海軍陸戰(zhàn)隊(duì)傷病員醫(yī)療后送鏈中唯一能承擔(dān)層級(jí)2 全部職責(zé)的正規(guī)力量。美國(guó)海軍陸戰(zhàn)隊(duì)現(xiàn)有4 個(gè)衛(wèi)生營(yíng),一營(yíng)和三營(yíng)配屬于太平洋艦隊(duì)陸戰(zhàn)隊(duì)的第一陸戰(zhàn)師和第三遠(yuǎn)征部隊(duì),二營(yíng)配屬于大西洋艦隊(duì)陸戰(zhàn)隊(duì)的第二遠(yuǎn)征部隊(duì),四營(yíng)配屬于作為后備力量的第四陸戰(zhàn)師。在戰(zhàn)場(chǎng)上,衛(wèi)生營(yíng)接受后勤戰(zhàn)斗單元的指揮。既設(shè)有營(yíng)指揮部,也下設(shè)了專(zhuān)業(yè)的勤務(wù)連。除交通、藥材等下屬勤務(wù)單元外,衛(wèi)生營(yíng)最核心的業(yè)務(wù)組織,是作為營(yíng)直屬單位的2 個(gè)手術(shù)排。每一個(gè)直接服務(wù)于一線部隊(duì)的戰(zhàn)斗后勤營(yíng),往往都與一個(gè)手術(shù)連同時(shí)部署,以保障團(tuán)一級(jí)的戰(zhàn)斗隊(duì)伍。戰(zhàn)斗后勤營(yíng)可以為手術(shù)連提供電力、交通等勤務(wù)資源,手術(shù)連的任務(wù)則是充分利用自己下屬的4 個(gè)手術(shù)排接收FRSS、STP 后送來(lái)的傷病員,并臨時(shí)留置歸自己負(fù)責(zé)保障的一線部隊(duì)的傷病員。由于手術(shù)排可以提供傷病員的途中救護(hù),衛(wèi)生營(yíng)和手術(shù)連都有能力實(shí)施MEDEVAC,將CASEVAC 至承擔(dān)層級(jí)4 職責(zé)的救治機(jī)構(gòu)。
3 對(duì)我海軍陸戰(zhàn)隊(duì)的啟示與建議
3.1 應(yīng)為我海軍陸戰(zhàn)隊(duì)籌建專(zhuān)業(yè)化的機(jī)動(dòng)衛(wèi)勤力量從美軍的配置情況來(lái)看,在海軍陸戰(zhàn)隊(duì)的前2 個(gè)救護(hù)層級(jí)中存在著FRSS、STP 等專(zhuān)門(mén)針對(duì)海軍或海軍陸戰(zhàn)隊(duì)的多種機(jī)動(dòng)衛(wèi)勤力量。當(dāng)前我陸軍的前沿外科手術(shù)隊(duì)建設(shè)方興未艾,我海軍艦艇部隊(duì)的醫(yī)院船醫(yī)療隊(duì)、編隊(duì)救護(hù)所醫(yī)療隊(duì)等機(jī)動(dòng)衛(wèi)勤力量的訓(xùn)練如火如荼,但專(zhuān)門(mén)針對(duì)海軍陸戰(zhàn)隊(duì)特殊作戰(zhàn)樣式和任務(wù)背景的機(jī)動(dòng)衛(wèi)勤力量建設(shè)工作尚未引起足夠的重視。在今后的建設(shè)中,我軍應(yīng)借鑒美軍對(duì)普通海軍醫(yī)院看護(hù)兵進(jìn)行強(qiáng)化培訓(xùn)以適應(yīng)陸戰(zhàn)隊(duì)需求、模仿陸軍前沿外科手術(shù)隊(duì)建設(shè)FRSS 的做法,對(duì)我海軍陸戰(zhàn)隊(duì)機(jī)動(dòng)衛(wèi)勤力量體系進(jìn)行新的設(shè)計(jì)論證,加速醫(yī)療增援組織模塊的設(shè)計(jì)研究[3],為建設(shè)目標(biāo)、力量構(gòu)成、編組模式等確立標(biāo)準(zhǔn),切實(shí)增強(qiáng)對(duì)我海軍陸戰(zhàn)隊(duì)的衛(wèi)勤綜合保障能力。
3.2 應(yīng)為我海軍陸戰(zhàn)隊(duì)構(gòu)建強(qiáng)協(xié)同的立體后送體系從美軍的后送層級(jí)來(lái)看,其海軍陸戰(zhàn)隊(duì)比常規(guī)的陸軍后送層級(jí)更少,越級(jí)后送的頻率更高,這說(shuō)明美軍已經(jīng)在實(shí)戰(zhàn)中認(rèn)識(shí)到,海軍陸戰(zhàn)隊(duì)一旦發(fā)生傷病員,傷情、病情的嚴(yán)重程度更高,從受傷地點(diǎn)到后送鏈末端實(shí)施傷病員醫(yī)療后送的難度也更大。我軍已經(jīng)初步完成了衛(wèi)生連等專(zhuān)業(yè)衛(wèi)勤隊(duì)伍的編制體制改革,但對(duì)聯(lián)合作戰(zhàn)衛(wèi)勤協(xié)同的認(rèn)識(shí)還有待加強(qiáng),尤其是對(duì)衛(wèi)勤保障從軍種向聯(lián)勤發(fā)展的跨域協(xié)同缺乏深層次的理解。海軍陸戰(zhàn)隊(duì)有其特殊性,只有依靠聯(lián)合指揮,基于每次具體的衛(wèi)勤保障行動(dòng)理順協(xié)同關(guān)系,利用空軍、陸軍等各軍種各類(lèi)衛(wèi)勤力量,有效組織,合理搭配,才能順利構(gòu)建起符合陸戰(zhàn)隊(duì)傷病員醫(yī)療后送真實(shí)需求的立體后送體系。基于目前的發(fā)展水平,應(yīng)先借助多方力量,以提高CASEVAC 能力為第一目標(biāo),以提高專(zhuān)業(yè)性MEDEVAC 能力為未來(lái)方向。
3.3 應(yīng)為我海軍陸戰(zhàn)隊(duì)創(chuàng)建高標(biāo)準(zhǔn)的衛(wèi)勤訓(xùn)練課程從美國(guó)海軍陸戰(zhàn)隊(duì)對(duì)一線救治能力的要求來(lái)看,他們對(duì)陸戰(zhàn)隊(duì)傷病員救治有著更高的時(shí)效要求,對(duì)醫(yī)療后送平臺(tái)的途中救護(hù)工作也有著更高的質(zhì)量要求。2015 年之前,美國(guó)海軍看護(hù)兵要先完成由美國(guó)陸軍負(fù)責(zé)訓(xùn)練及考核的飛行軍醫(yī)課程,才有資格參加海軍陸戰(zhàn)隊(duì)的戰(zhàn)斗任務(wù),在其傷病員管理層級(jí)中承擔(dān)層級(jí)1 的職責(zé)。多年來(lái),該類(lèi)課程的內(nèi)容不斷拓展,目前已將能力標(biāo)準(zhǔn)提高到了重癥監(jiān)護(hù)人員的水平[4]。雖然從2015 年開(kāi)始至今海軍看護(hù)兵沒(méi)有對(duì)任何傷病員實(shí)施過(guò)空運(yùn)醫(yī)療后送,培訓(xùn)壓力已大幅下降,不再需要前往陸軍接受大規(guī)模培訓(xùn),但美國(guó)海軍寧愿改為由海軍自己提供相關(guān)課程,也要維持此類(lèi)訓(xùn)練[5]。顯然,他們非常重視以提高海軍陸戰(zhàn)隊(duì)保障能力為目標(biāo)的衛(wèi)勤訓(xùn)練,即使短期內(nèi)沒(méi)有現(xiàn)實(shí)需求也不允許停止訓(xùn)練。我軍在不斷推進(jìn)戰(zhàn)傷救護(hù)實(shí)戰(zhàn)化訓(xùn)練的同時(shí)[6],還要持續(xù)關(guān)注參與保障海軍陸戰(zhàn)隊(duì)的非建制性力量中的衛(wèi)勤人員。他們雖然不屬于海軍陸戰(zhàn)隊(duì)編制,不在海軍陸戰(zhàn)隊(duì)所屬機(jī)構(gòu)進(jìn)行培訓(xùn),但必須接受標(biāo)準(zhǔn)更高、要求更嚴(yán)、時(shí)效性更強(qiáng)的衛(wèi)勤訓(xùn)練,時(shí)刻準(zhǔn)備為我海軍陸戰(zhàn)隊(duì)提供高質(zhì)量的衛(wèi)勤保障。

