創意折疊桌的最優設計加工參數研究
江偉 劉嬋

摘 要:該文采用2014年全國大學生數學建模競賽B題的數據,在對折疊桌的穩定性、用料等方面做出科學性分析的基礎上,建立以用料和桌面重心為優化目標的優化模型Ⅰ,并使用MATLAB編程求解,結果為:最外側桌腿的長度為73cm,平板的長度為150cm,最外側桌腿與地面的夾角為66.7°,并使用該模型對問題一中折疊桌進行了優化,驗證了優化模型Ⅰ的正確性。另外,設計了一個桌面形狀為橢圓形的創意平板折疊桌并使用MATLAB編程求解出最優化加工參數,并使用Solidwokes軟件畫出了該折疊桌的動態變化圖。
關鍵詞:優化模型 最優加工參數 穩固性
中圖分類號:TS665 文獻標識碼:A 文章編號:1672-3791(2015)02(c)-0045-02
1 優化目標分析
分析折疊桌的重心、桌腿的開槽的長度、桌腳與地面的夾角之間的關系,可發現如下規律。
(1)平板折疊后重心越低,即鋼筋的位置越低,穩定性越好。
(2)平板折疊后開槽長度越長,穩定性越好,但用料會增加。
(3)平板折疊后桌腳與地面夾角越大,穩定性越好,但用料增多。
綜上所述,可知折疊桌的穩定性和用料不可能同時達到最優,只能根據實際情況設計出最優模型。
2 優化模型的建立與求解
首先先找到平板長度以及第一根桌腿邊緣到鋼筋的長度(也可以看成是鋼筋的高度)的約束條件,不失一般性的情況下,假設桌面厚度為=3,為保證木條根數為整數,故取=2cm。
約束條件①:
由于三角形的斜邊大于直角邊可以得到如下關系:
(1)
約束條件②:
想要穩固性好,但用料又最省,即最中間木條桌腿的長度等于第一根桌腿從桌面到鋼筋的長度,也就是說滿足方程組(2)。
(2)
約束條件③:
畫出折疊桌第一根桌腿與最中間桌腿的幾何投影圖如圖2。
當桌腳與地面的角度θ與半徑固定時,在與垂直情況下距離最短,折疊桌的用材最省,參數滿足方程(3)。
(3)
由此可得折疊桌設計加工參數優化模型:
約束目標:
約束條件:
(Ⅰ)
當桌面高度和平板尺寸,木條寬度給定時,可以找到使桌面達到最穩定狀態時鋼筋的位置,例如,在問題一中,=53cm,平板尺寸為120×50×3,=2.5cm由(2)式可求出≈17.44cm,這時鋼筋的位置最低,折疊桌的重心也最低,因而穩固性最好,但相對來說開槽長度是最長的,在第一問中給出的折疊桌從桌腿邊緣到鋼筋的長度為28.75>17.44,因此穩固性沒有達到最優,但開槽長度較短,加工較為方便。
現在我們給定=70cm,=80cm則由式(1)得出平板長度a>138cm,利用MATLAB軟件編程求解優化模型Ⅰ可得:=73cm(最外側桌腿的長度),=150cm(平板的長度),=66.7°(最外側桌腿與地面的夾角),也就是說在給定平板寬度和桌面高度時,上述結果為用料相對最省、穩固性最好的折疊桌面設計加工參數最優值。
3 創意折疊桌設計
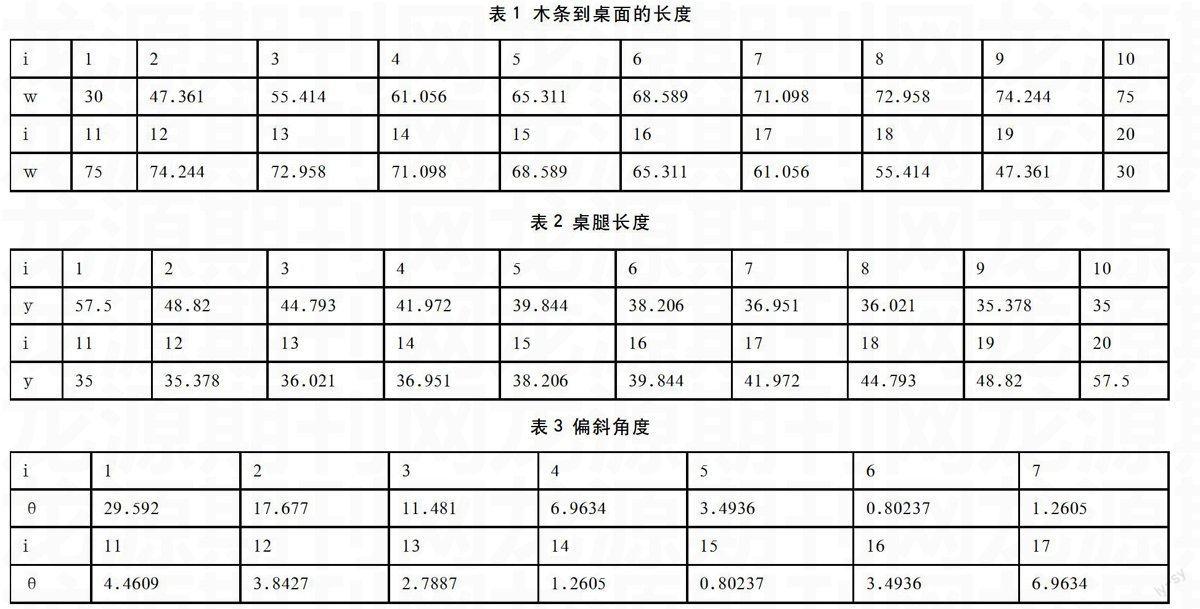
要根據用戶給定指標設計疊桌邊緣線形狀(如設計成橢圓形等形狀),考慮到制作成本、實用性、美觀程度和穩定性的因素,設計了一款桌面形狀為橢圓形的折疊桌:平板長度為145cm,寬度為50cm,桌面高度為53cm時,使用MATLAB軟件編程求解可得橢圓形折疊桌最優加工參數見表1、2、3。
為了連續的觀察折疊桌折疊時的變化,使用SolidWorks軟件,使用上述設計加工參數數據,可畫出該折疊桌的動態變化過程的示意圖,見圖3。
4 結語
該文根據客戶的設計要求,在對折疊桌設計加工參數做優化時綜合考慮了用料省和穩固性好這兩個因素來建立模型,使用軟件編程求解模型的最優參數值,具有很強的實用性和推廣性。
參考文獻
[1] 汪曉銀,周保平.數學建模與數學實驗[M].北京:科學出版社,2011.
[2] 劉衛國.MATLAB程序設計教程[M].北京:中國水利水電出版社,2010.
[3] 董辰輝,彭雪峰.MATLAB2008全程指南[M].北京:電子工業出版社,2008.

