與正整數的k次冪補數有關的恒等式

(渭南師范學院 數學與信息科學學院, 陜西 渭南 714000)

· 基礎學科·

與正整數的k次冪補數有關的恒等式

王明軍

(渭南師范學院 數學與信息科學學院, 陜西 渭南 714000)

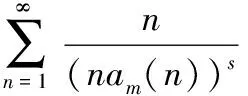
k次冪補數；Zeta函數；恒等式

1 引言及結論

本文用初等方法研究了補數序列的一些性質,得到了補數序列的幾個恒等式,即就是下面的定理：

定理1 對任意復數s，其中Res≥2,則有恒等式

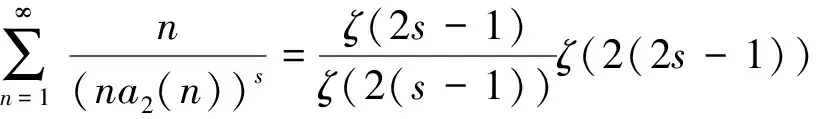
(1)

其中ζ(s)表示Zeta函數。

定理2 對任意復數s，其中Res≥2,則有恒等式

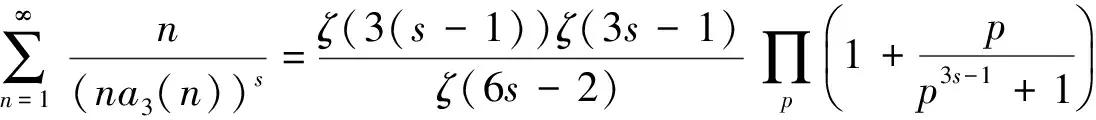
(2)

其中：ζ(s)表示Zeta函數；p為素數。

定理3對任意復數s，其中Res≥2,則有恒等式

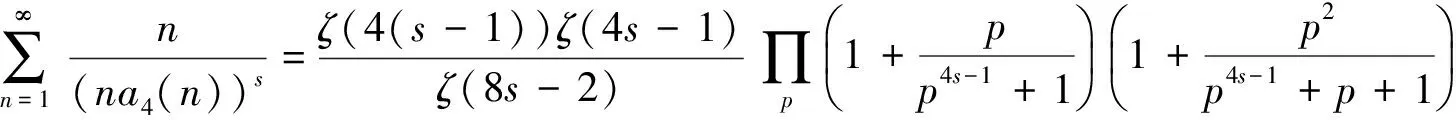
(3)

其中：ζ(s)表示Zeta函數；p為素數。

2 定理的證明

2.1 定理1的證明

證明對任意的正整數n,可唯一表示為n=u2v,其中u、v均為正整數，且v是無平方因子數,μ(n)表示Mobius函數，所以有

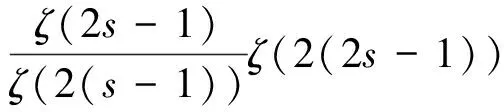
(4)

2.2 定理2的證明

證明對任意的正整數n,又可唯一表示為n=u3v2w,其中u、v、w均為正整數，v、w均無大于1的平方因子，且(v,w)=1；所以有

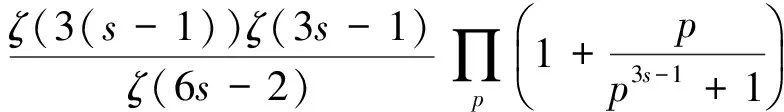
(5)

2.3 定理3的證明

證明

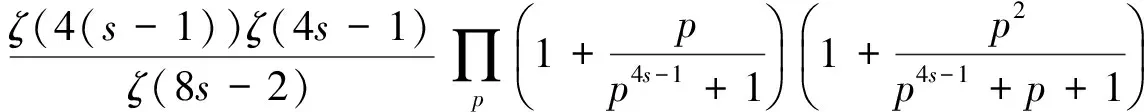
(6)

[1] Smarandache F. Only Problems,Not Solutions[M].Chicago： Xiquan Publ House,1993.

[2]劉紅艷,茍素.關于F.Smarandache的一個問題[J].延安大學學報：自然科學版，2001，20(3):5-6.

[3]王陽.關于三次方冪補數的均值[J].純粹數學與應用數學,2002 ,18 (3) ：137-139.

[4]王明軍，李海龍.關于平方補數的幾個均值公式[J].哈爾濱師范大學學報：自然科學版，2008 ,24 (1):19-21.

[5]Tom M. Apostol. Introduction to Analytic Number Theory [M]. New York：Springer Verlag,1976.

(編校：葉超)

Identitiesonthek-thPowerComplements

WANG Ming-jun

(DepartmentofMathematicsandInformationScience,WeinanTeachersUniversity,Weinan, 714000)

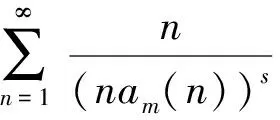
k-thpower complement number; Zeta function; identities

2013-11-25

陜西省自然科學基礎研究計劃項目(2014JM2-1004)；陜西省(數學)扶持學科建設項目。

王明軍(1972—)，男，副教授，碩士，主要研究方向為數論。

O156.4

：A

：1673-159X(2015)03-0094-03

10.3969/j.issn.1673-159X.2015.03.019