感應線圈車輛檢測器數據的預處理方法研究

陶漢卿

(柳州鐵道職業技術學院電子工程系，廣西 柳州 545616)

感應線圈車輛檢測器數據的預處理方法研究

陶漢卿

(柳州鐵道職業技術學院電子工程系，廣西 柳州 545616)

為提高感應線圈車輛檢測器的感應曲線特征提取和交通信息檢測的準確率，文章以感應線圈車輛檢測器的感應曲線信號為基礎，研究了感應線圈信號曲線的預處理方法，并通過基于中值濾波和聚類分析的基頻漂移抑制實驗驗證，表明該預處理方法能很好地抑制噪聲，達到了較為理想的效果，具有極大的應用前景和推廣價值。

車輛檢測器；中值濾波；聚類分析；數據預處理

0 引言

隨著經濟和社會的高速發展，交通問題越來越突出，智能交通系統(ITS)運用計算機技術、網絡技術、自動控制技術解決交通問題，提高交通的運輸能力和效率，要實現智能交通系統的管理和控制，交通信息獲取是基礎，是智能交通系統中的關鍵部分。應用于交通信息采集的設備很多，如感應線圈、視頻監控、紅外線、激光信息采集，感應線圈于同類設備比較，具有穩定和可靠性好、性價比和檢測精度高、使用時間長和技術成熟等優勢。本文以感應線圈車輛檢測器采集到的數據為基礎，對感應曲線數據預處理算法進行了研究。

目前感應線圈交通信息采集的技術已經相當成熟，但利用其采集的數據進行處理分析的研究還很有限，提升空間較大，因此近年來吸引了不少研究者的關注。而現有的基于感應線圈的感應數據曲線的預處理技術還很少，基線漂移抑制具有不同的解決方案，如基于FIR和IIR濾波器的基線漂移抑制法、基于自適應濾波器的基線漂移抑制方法、運用小波分解方法抑制基線漂移，但是這些方法具有不同的缺陷：基于FIR和IIR濾波器的基線漂移抑制法，不適用于噪聲頻率超過截止頻率的情況[1]；基于自適應濾波器的基線漂移抑制方法需要參考一段時間內采集到的噪聲信號，而該信號與所需要采集的信號沒有關聯[2]；小波分解方法需要對基線移頻信號進行分解，然后再濾波，對于和噪聲信號接近時的采集信號，該方法無法準確濾波。在平滑濾波方面，文獻[4]提出了“五點三次”的方法對感應線圈曲線數據進行平滑濾波，平滑后的曲線很好地揭示了信號的主要起伏特征(突出波峰、波谷)，但是還可以進一步改進。因此，有必要對感應數據曲線的預處理技術進行深入的研究。

1 感應線圈數據曲線感應數據預處理需求分析

本文以感應線圈車輛檢測器的感應曲線信號為基礎，對感應線圈數據處理分析技術進行深入研究。各種車輛經過感應線圈時產生的典型信號曲線如圖1所示，其中橫坐標為時間，縱坐標為頻率變化值[4]，感應線圈數據是離散的時間序列，具有隨機性。

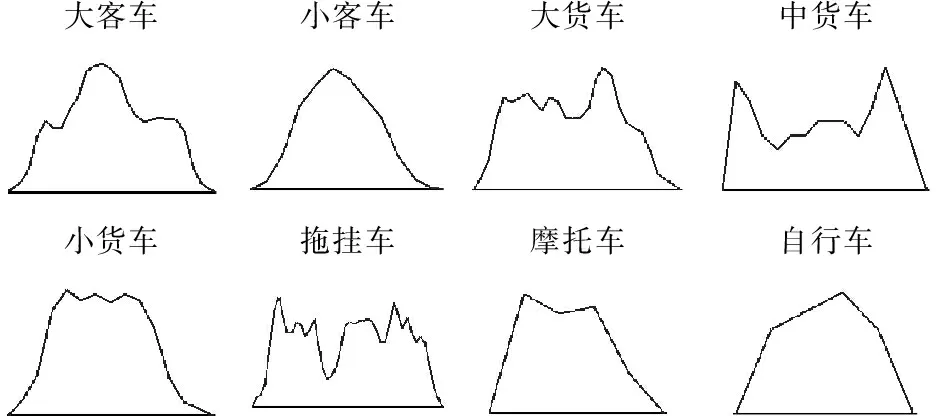
大客車小客車大貨車中貨車小貨車拖掛車摩托車自行車

圖1 常用車識別典型曲線圖

由數據采集系統獲取的感應數據是最原始的，其蘊含了各種不同成因下的干擾信號，包括長期工作后感應線圈的老化變形，溫度、電磁場等環境因素的影響，倘若直接利用這些數據進行實時交通信息處理和分析，必然導致較差的效果，嚴重影響交通信息檢測的精度和結果的可靠性。因此，在實時交通信息處理和分析步驟之前，必須對原始數據進行一系列的預處理，剔除不同干擾因素的噪聲信號，提取原始數據的真實信息。感應線圈曲線數據預處理的流程如圖2所示。

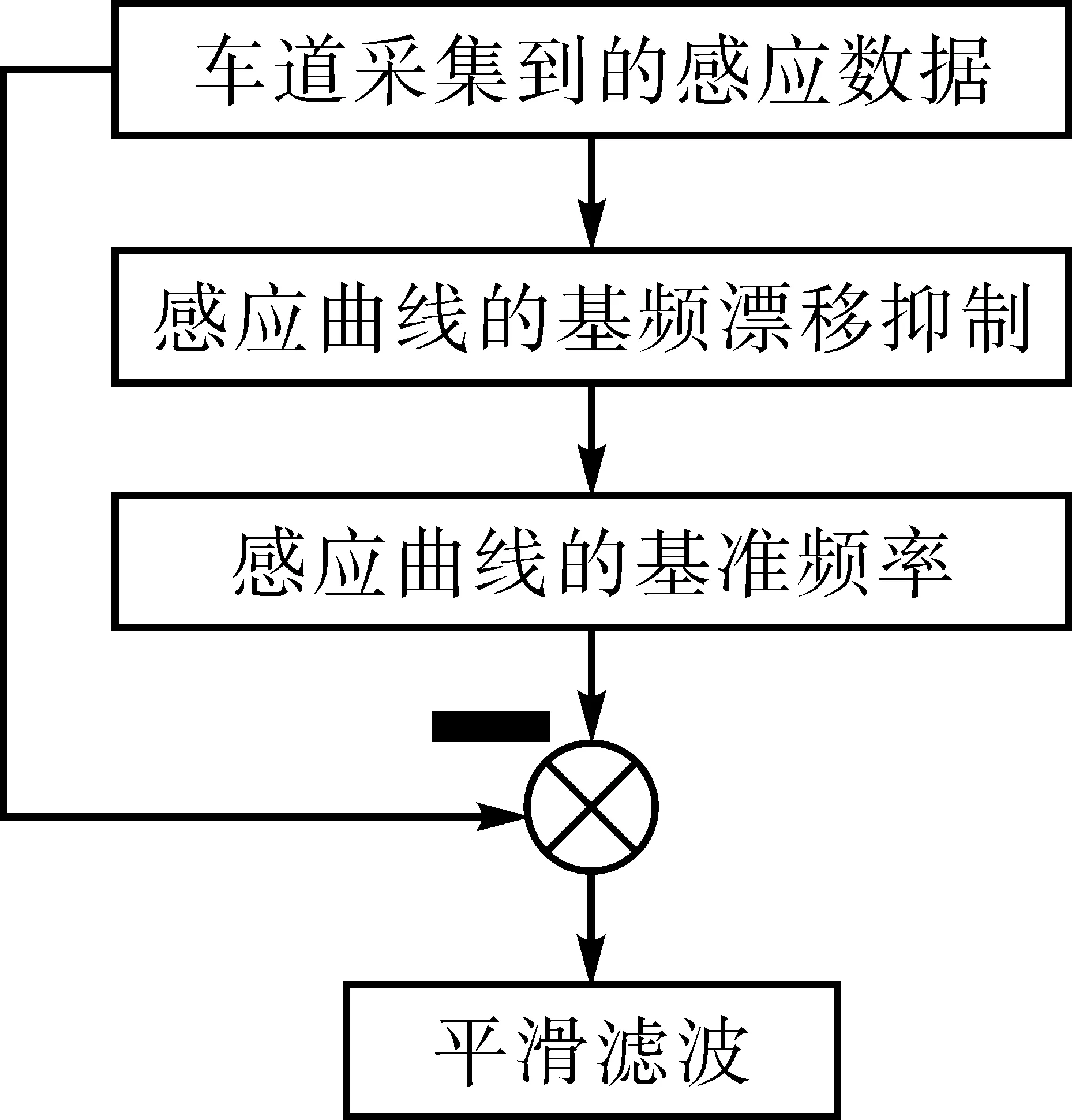
圖2 感應數據預處理流程圖

(1)感應線圈車輛檢測器采集原始數據，對噪聲和信號進行壓縮處理；

(2)采用聚類分析融合分離和剔除出無效信號，用中值濾波的方法獲取準確的車輛檢測器感應數據；

(3)采用chebyshev多項式擬合的方法進行平滑濾波處理，得到感應曲線的準確特征。

2 感應線圈車輛檢測器數據的預處理方法

2.1 中值濾波的算法

傳統中值濾波的算法[5]是：建立一個長度為N=2L+1(L=1，2，…，n)，N為奇數，組成濾波窗口，移動離散信號序列窗口中心，采用升序或降序的方式排列每個窗口的數據；把原中心位置的值更換為排序所得的中值，該算法窗口數據排序頻繁，速度慢，實時性低。

2.2 基于中值濾波和聚類分析的基頻漂移抑制方法

本文在傳統中值濾波算法的基礎上進行改進，對車輛檢測器的基頻漂移進行抑制：利用一個長度為N的時間窗沿著時間軸作聚類分析，把窗內的N個原始數據序列x(n)，…，x(n+N-1)分成基頻信號和“異常信號”兩個簇(通常基頻類的聚類中心值較小，而“異常信號”類的聚類中心值較大)，以基頻信號序列中第K個位置為中心，取2L+1個數據，建立一個滾動窗口，設窗口數據為：W[i](i=0，1…，2L+1)，將窗口的前2L+1個數據進行降序排序放到數組F[i](i=0，1…L)，則中值為F1[L]，更新基頻值為中值點，向橫坐標時間軸移動窗口，然后插入前一個窗口數據的中值F1[L]作為新數據，為保持窗口的長度2L+1不變，需要剔除原窗口中最左端的數據，然后重復上述的步驟，對新窗口進行聚類分析，新窗口為2L+1個數據序列x(n+1)，…(x+N)，根據以下公式(1)～(4)對窗口的后2L+1數據進行比較判斷[6]，F2[L]為窗口后2L+1個數據的中值，作為該窗口的新基頻值，通過窗口和中值的滾動計算，選取，可以跟蹤基頻，從而實現基頻漂移抑制。

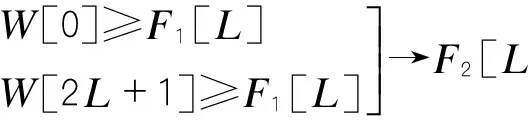
(1)

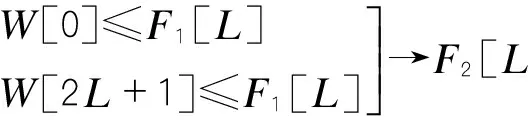
(2)

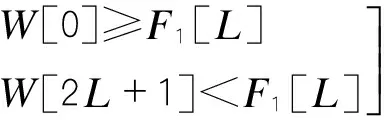
(3)

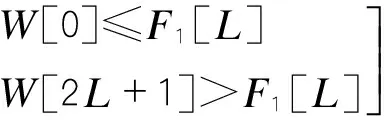
(4)

正確地選取濾波窗口的大小N直接影響基頻漂移跟蹤的效果[7]。N值太小，會影響聚類的準確性，算法失去了基頻漂移抑制的效果；N值過大，濾波窗口過大，會導致時間間距太大，計算的基頻聚類中心值與當前值具有一定的差距，基頻漂移無法進行跟蹤。根據實驗計算，N一般取7～11(L一般取3～5)。

2.3Chebyshev多項式

Tn(x)=cos(narccosx)

(5)

該式被稱為切比雪夫(Chebyshev)多項式。

切比雪夫多項式具有以下性質[8]：

(1)正交性

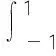
(6)

(2)遞推關系

Tn+1(x)=2xTn-Tn-1(x)，n≥1

(7)

由T0(x)=1，T1(x)=x遞推可得：

T2(x)=2x2-1

T3(x)=4x3-3x

T4(x)=8x4-8x2+1

T5(x)=16x5-20x3+5x

T6(x)=32x6-48x4+18x2+1

(8)

顯然，Tn(x)的首項系數an=2n-1(n≥1)。

(3)奇偶性

當n為奇數時，Tn(x)為奇函數；當n為偶數時，Tn(x)為偶函數。即Ln(-x)=(-1)nLn(x)。

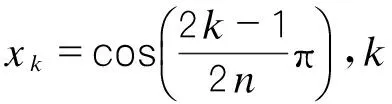
2.4 感應數據的Chebyshev多項式擬合

應用Chebyshev多項式擬合感應數據的步驟如下：

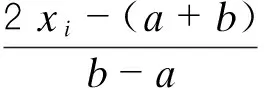
(9)

(2)根據性質2中的式(8)，計算

T0(ti)=1，T1(ti)=ti，i=1，…，m，

(10)

以及

T2(ti)，…，Tn(ti)，i=1，…，m；

(11)

(3)計算內積

(12)

(13)

(4)求法方程組

[(Tj，Tk)]c=b

(14)

的解c=[c0，c1，…，cn]T，其中b=[(y，T0)，(y，T1)，…(y，Tn)]T；

(5)由區間變換

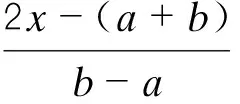
(15)

計算得到t值后，相應計算Tk(t)的值(k=0，1，…，n)。

(6)感應數據的多項式擬合為

f(x)=c0T0(t)+c1T1(t)+…+cnTn(t)。

(16)

在感應數據時間序列個數>m+1(m>0)的情況下，都能夠擬合到一個n階Chebyshev多項式，該Chebyshev多項式擬合方法要求m遠大于n，這對于感應線圈數據信號序列是普遍適合的。擬合的階數越高，擬合點越準確，由于高階次會增加計算量，數據點吻合好不代表擬合合理，但是并非擬合的階次越高越好[9]。實驗證明階數≤6效果最好，所以本文階數取n=5。

3 實驗分析

基于中值濾波和聚類分析的基頻漂移抑制實驗如圖3所示。

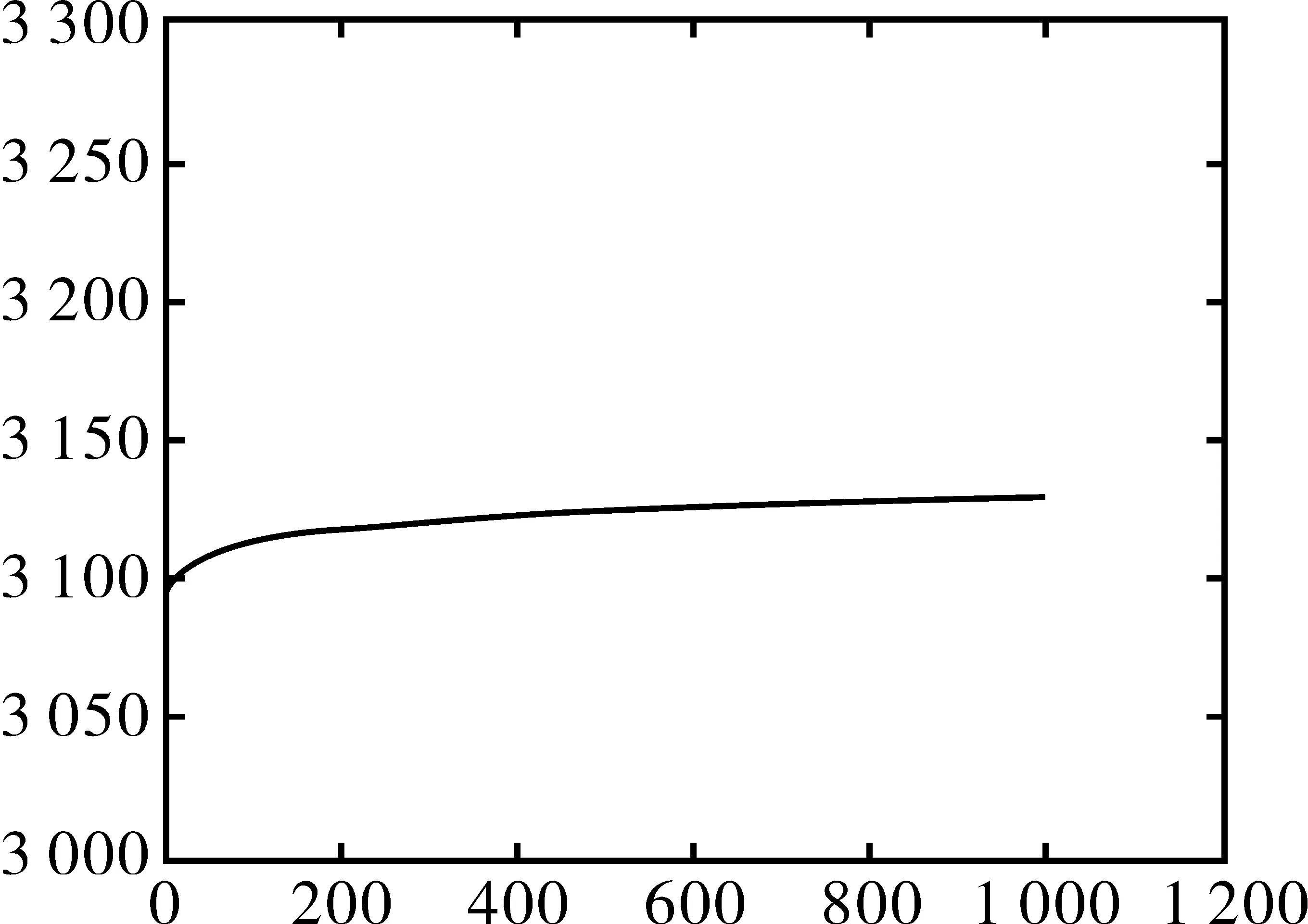
(a)基于中值濾波和聚類分析的基頻漂移跟蹤曲線

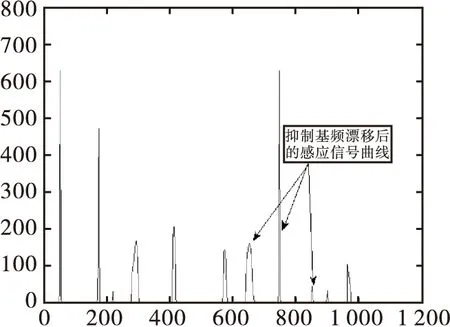
(b)基頻漂移抑制后的車輛感應曲線

從圖3(b)可以看出，感應信號較強的車輛(如小轎車)，其頻率數據(單位為HZ)變化峰值>600，而感應信號較弱的車輛(如自行車)，其頻率數據變化峰值很小，一般在30左右，同時也可以從圖3(a)中看出，基頻漂移是緩慢變化的，但是變化的幅度在一定時間內超過了感應信號較弱的車輛的幅值。因此需要對基頻漂移進行跟蹤和抑制。

采集到的原始信號序列為X1=[3 46 103 188 201 193 182 190 192 171 53 22 18 8 29 48 100 170 173 176 166 167 173 185 178 68 36 17 8]；

經過中值濾波和聚類分析的基頻漂移進行基頻漂移后為X2=[3 46 98 189 201 183 185 190 192 150 55 22 18 8 20 50 102 170 173 168 171 167 170 175 178 70 33 17 8]；

根據理論計算值為X3=[3 46 98 188 201 183 182 190 192 150 53 22 18 8 20 48 100 170 173 168 166 167 173 175 178 68 33 17 8]；

利用公式S=max{Xi，j[k]-X3[k]}(i，j=1，2，k=1，2，3…)計算最大誤差。采集到的原始信號最大誤差為：X1[10]-X3[10]=171-150=21；中值濾波和聚類分析的基頻漂移抑制后最大誤差為：X2[21]-X3[21]=171-166=5。

實驗結果表明：中值濾波和聚類分析的基頻漂移抑制后最大誤差僅為5，比采集到的原始信號最大誤差小很多，提高了采集的感應線圈車輛傳感器數據的準確性，因此基于中值濾波和聚類分析的基頻漂移抑制方法，能自動區分車輛感應數據和基頻漂移數據的能力，并且可以利用基頻信號聚類中心實時更新當前基頻值。故能有效抑制基頻漂移，并且成功分離車輛感應信號，達到較理想的效果。

經過抑制基線漂移后，對采集到的感應線圈數據信號，進行Chebyshev多項式擬合平滑濾波，結果如圖4所示。實驗結果表明：平滑濾波后能更為準確地反映感應曲線的特征，所以該方法是有效的。

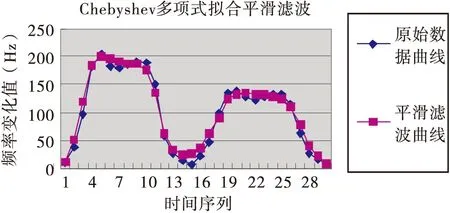
圖4 感應曲線平滑濾波圖

4 結語

本文闡述的感應線圈數據的預處理方法能很好地抑制基頻漂移，平滑濾波后的數據曲線進一步揭示了信號的主要起伏特征(突出波峰、波谷)，這對于提高感應線圈車輛檢測器的抗干擾能力具有重要的意義，平滑濾波使得曲線的特征提取更加準確，從而提高了車流量、車速、車型等交通信息的檢測精度。

[1]鄒 波，周 遠.一種濾除基線漂移和工頻干擾的數字濾波算法[J].深圳職業技術學院學報，2005(4)：3-5.

[2]李 剛，劉 巍，虞啟璉，等.抑制工頻干擾及基線漂移的快速算法[J].中國生物醫學工程學報，2000，19(1)：63-65.

[3]李小燕，王 濤，馮煥清，等.基于小波變換的自適應濾波器消除ECG中基線漂移[J].中國科學技術大學學報.2000，30(4)：450-454.

[4]林培群.道路交通參數及交通事件智能檢測關鍵技術研究[D].廣州：華南理工大學，2008.

[5]林成森.數值計算方法[M].北京：科學出版社，2005.

[6]危疆樹.中值濾波算法及其并行化研究[J].福建電腦，2008(7)：101-101.

[7]YINL，YANGR，GABBOUJM，NEUVOY.Weightedmedianfilters：atutorial[J].IEEETransCircuitsSystem，1996，43(3)：157-192.

[8]張可村，趙英良.數值計算的算法與分析[M].北京：科學出版社，2002.

[9]徐宜會，趙寶貴.Matlab在數據擬合中的應用[J].科技廣場，2007，34(2)：169-170.

Study on the Preprocessing Methods of Induction Coil Vehicle Detector Data

TAO Han-qing

(Department of Electronic Engineering，Liuzhou Railway Vocational and Technical College，Liuzhou，Guangxi，545616)

To improve the accuracy of induction curve feature extraction and traffic information detection for the induction coil vehicle detector，based on induction curve signal of induction coil vehicle detector，this article studied the preprocessing methods of induction coil signal curve，and through the base fre-quency drift suppression experiments based on median filtering and cluster analysis，it showed that this preprocessing method can suppress the noise，reaching more satisfactory results，thus it has great ap-plication prospects and promotional value.

Vehicle detector；Median filtering；Cluster analysis；Data preprocessing

陶漢卿，碩士，講師，從事智能交通系統方面的教學科研工作。

2013年度廣西高校科學技術研究項目“城市軌道交通車載測速定位裝置的研制”(編號：2013YB358)

U

A

10.13282/j.cnki.wccst.2015.07.015

1673-4874(2015)07-0063-05

2015-06-06