用數學思想引領高三復習教學——以“函數與方程思想”破解“函數零點與方程的根”為例

☉江蘇省清浦中學 吳洪生

2015年江蘇高考數學《考試說明》將“函數與方程”考點由過去的A級要求提升為B級要求，足見“函數與方程”在高考中的重要地位.函數與方程是兩個不同的概念，但它們之間有著十分密切的聯系.很多函數問題需要用方程的知識與方法來支持；很多方程的問題，需要用函數的知識與方法去解決.

函數與方程思想，既是函數思想與方程思想的體現，也是兩種思想綜合運用的體現，本質是實現函數與方程的相互轉化.一個函數若有解析式，那么這個解析式就可看成一個方程，如函數y=f（x）也可看成二元方程f（x）－y=0；反之，一個二元方程，兩個變量存在著對應關系，如果這個對應關系是函數，那么這個方程就可看成函數.

一、教學目標要求

（1）理解并掌握“一個定理”、“兩個轉化”.

“一個定理”即函數零點存在定理：條件①f（x）在區間［a，b］上連續；②f（a）·f（b）＜0.結論：存在c∈（a，b），使得f（c）=0.

兩個轉化：①零點與方程的根的相互轉化：函數y=f（x）的零點?方程f（x）=0的根；②零點與函數圖像與x軸的交點或兩個函數圖像的交點的相互轉化：函數y=f（x）的零點?函數y=f（x）的圖像與x軸交點的橫坐標；函數y=f（x）－g（x）的零點?函數y=f（x）與y=g（x）圖像交點的橫坐標.特別地，如果f（x）=g（x）－a，則函數y=f（x）的零點?函數y=g（x）的圖像與直線y=a交點的橫坐標.透徹理解“函數的零點、方程的根、函數圖像交點的橫坐標”的意義是實現上述轉化的關鍵.

（2）通過復習使學生強化對函數與方程相互轉化的認識與理解，進而解決函數的零點、方程的根及相關參數問題.提高學生分析問題、解決問題的能力.

二、把握函數與方程思想的內涵

函數問題的方程思想，方程問題的函數視角，是函數與方程思想在處理數學問題時的具體體現.

（一）從函數視角研究方程根的問題

函數思想是對函數內容在更高層次上的抽象、概括與提煉，是通過建立函數，運用函數的圖像、性質去分析問題、解決問題.函數思想不僅僅是用函數的方法研究問題，更重要的是產生函數的方法，上升到思想高度主動思考問題.方程問題的函數視角就是利用函數的圖像、性質來研究方程的根及其范圍問題.

1.用函數圖像研究方程根的問題

利用導數知識畫出h（x）的圖像，如圖1，h（x）=1及h（x）=－1各有2個實數根.所以方程|f（x）+g（x）|=1的實根個數為4.

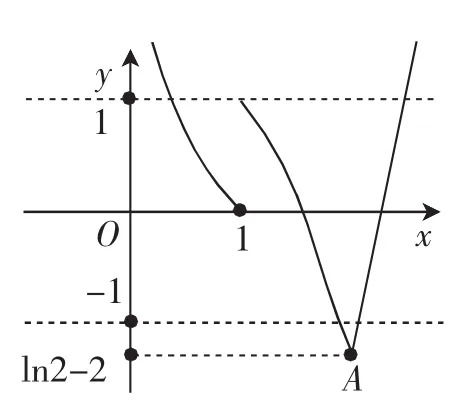
圖1

點評：由函數的零點、方程的根、圖像的交點三者之間的轉化關系可知，圖像法是解決方程根的問題的最常用方法，圖像也是它們之間聯系的橋梁.本題函數h（x）的圖像比較難畫，需要綜合運用函數與導數等知識.

2.用函數奇偶性研究方程根的問題

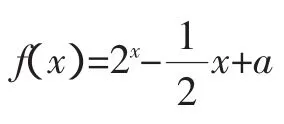
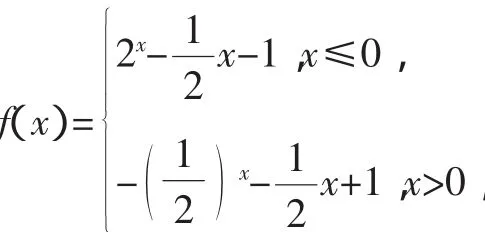
點評：奇函數的圖像關于原點對稱，偶函數的圖像關于y軸對稱，函數圖像與x軸正半軸有交點必與負半軸有交點，因此，對于奇、偶函數零點的研究，往往只需考慮大于0或小于0的零點，便知另一側的零點情況.

3.用函數對稱性研究方程根的問題

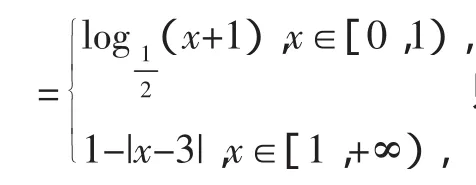
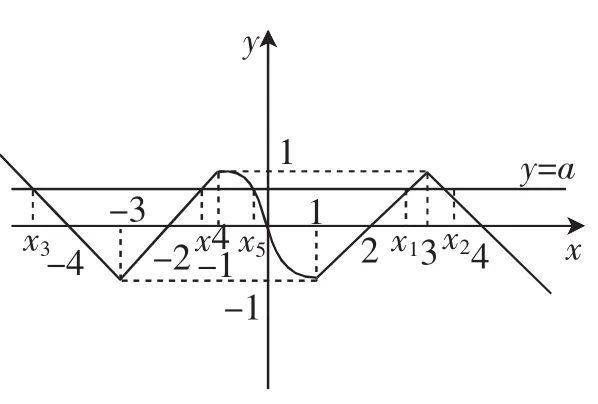
圖2

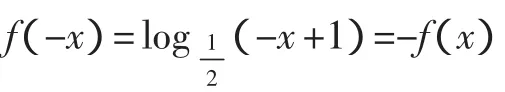
點評：本題三次應用對稱關系，函數本身是奇函數，其圖像關于原點對稱，兩次局部應用軸對稱，從而把求5個根和的問題轉化為求x5.輕松解決了貌似很難的問題.

4.用導數研究方程根的問題

例4 已知方程ax3－3x2+1=0存在唯一的根x0，且x0＞0，則實數a的取值范圍是_______.

解析：構造函數f（x）=ax3－3x2+1.

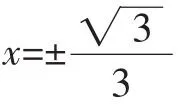
若a＞0，則f（－1）=－a－2＜0，f（0）=1＞0，所以f（x）存在負的零點，不合題意.

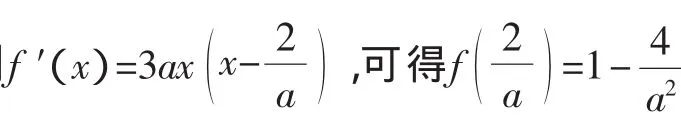
綜上，a的取值范圍是（－∞，－2）.

點評：本題首先將方程根的問題轉化為函數零點問題，借助導數勾畫函數草圖，依題意可知f（x）的極小值大于0，從而確定a的取值范圍.

5.用函數伸縮變換研究方程根的問題

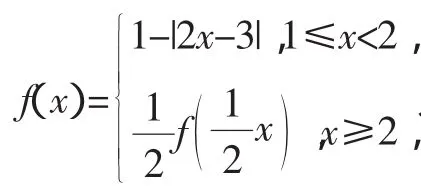
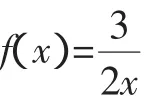
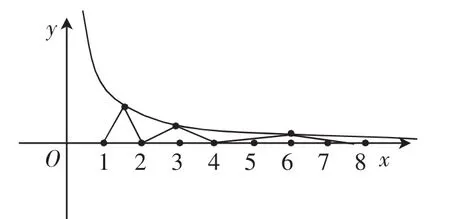
圖3

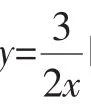
注意：（1）f（1）=f（2）=f（22）=f（23）=…=f（210）=0；

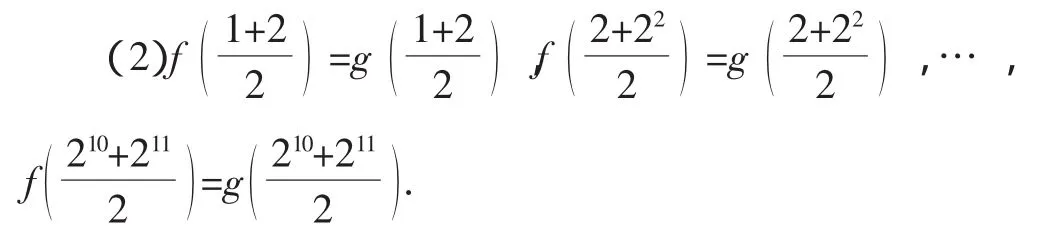
所以，兩函數圖像共有11個交點，方程2xf（x）－3=0在區間（1，2015）上有11個根.

點評：本題的本質是借助函數圖像研究方程的根，但作函數圖像包含圖像的伸縮變換，因此作圖較為困難，必須熟練掌握伸縮變換規律.

6.用函數單調性研究方程根的問題

例6 設函數f（x）=x3+2x2－4x+2a.

（1）求函數f（x）的單調區間；

（2）關于x的方程f（x）=a2在［－3，2］上有三個相異的實根，求a的取值范圍.

解析：（1）f′（x）=3x2+4x－4.

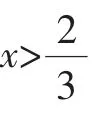
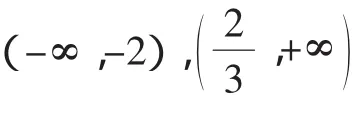
（2）由f（x）=a2?x3+2x2－4x－a2+2a=0，

構造函數g（x）=x3+2x2－4x－a2+2a.

所以g′（x）=3x2+4x－4.

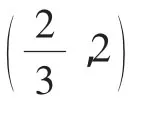
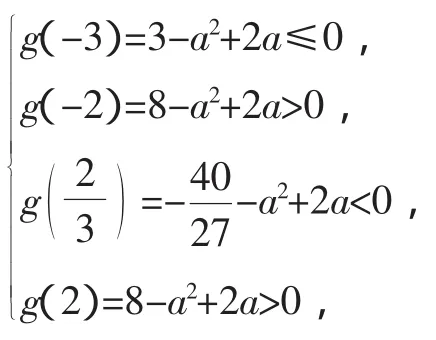
解得－2＜a≤－1或3≤a＜4.

點評：（1）先求f′（x），由f′（x）=0求出極值點，再討論單調性；（2）利用（1）及函數f（x）的大致圖形，找到滿足題設的a的條件.

7.用函數周期性研究方程根的問題

例7 定義在R上的函數f（x）滿足f（x）+f（x+5）=16，當x∈（－1，4］時，f（x）=x2－2x，則函數f（x）=0在［0，2013］上的根的個數是_______.

解析：由f（x）+f（x+5）=16，可知f（x+5）+f（x+10）=16，則f（x）=f（x+10），所以f（x）是以10為周期的周期函數.在一個周期（－1，9］上，函數f（x）=x2－2x在x∈（－1，4］內有3個零點，在x∈（4，9］內無零點，故f（x）在一個周期上僅有3個零點，由于區間（3，2013］中包含201個周期，又x∈［0，3］時也存在一個零點x=2，故f（x）=0在［0，2013］上的根的個數為3×201+1=604.

點評：周期性是函數的一種重要性質，一般來講，當所研究的區間相對較長時，題目往往與周期性有關.

（二）用方程思想研究函數的零點問題

方程思想就是突出研究已知量與未知量之間的等量關系，通過設（未知量）、列（方程（組））、解（方程（組））等步驟，達到求值目的的解題思路和策略，它是解決各類計算問題的基本思想.函數中的零點問題或兩個函數圖像的交點問題，常常化動為靜，轉化為方程的根來解，這就是函數問題的方程思想.

1.可通過直接解方程研究函數的零點問題

解析：令f（x）=t，方程f（t）－1=0的根為t1=0，t2=2，由f（x）=0，得x1=1；由f（x）=2，得x2=4.故有2個零點.

點評：直接求零點，令f（x）=0，如果能求出解，則有幾個解就有幾個零點.

2.可通過三角方程研究函數的零點問題

例9 （2012年高考湖北文）函數f（x）=xcos2x在區間［0，2π］上的零點個數為________.

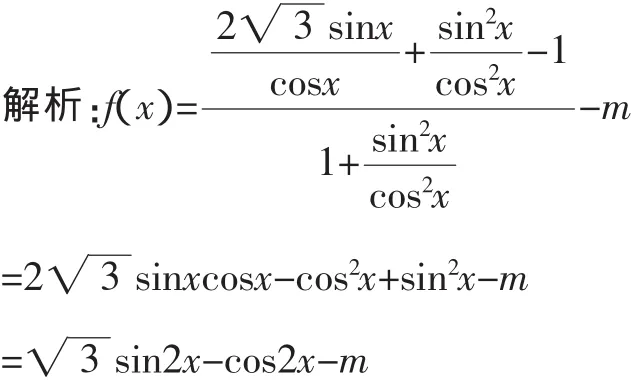
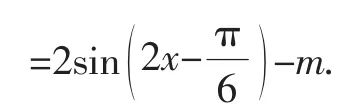
點評：三角函數的零點相對于我們常見的初等函數的零點要復雜一些，需要綜合運用三角函數的圖像、特殊值、取值范圍等知識.例9主要考查三角函數特殊值，例10綜合考查三角變換、輔助角公式、取值范圍、函數零點等考點.

3.可通過方程運算研究函數的零點問題

A.x1x2＜1 B.x1x2＞x1+x2

C.x1x2＜x1+x2D.x1x2=x1+x2

4.可用二次方程根的分布研究函數的零點問題

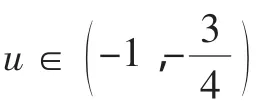
圖4

點評：函數是方程與不等式的“中介”，它們既有區別，又聯系緊密.本題主要是通過二次方程根的研究，來探究函數的零點，而研究二次方程根的分布，又依賴于不等式理論的支撐.本題是對函數與方程的綜合考查.

三、總結提煉，登高望遠

高三復習的主要目的就是提煉并建構數學思想方法體系，使解題策略與方法明確化、系統化.復習課的首要任務是把學生先前所學的知識連成線、鋪成面、織成網，實現融會貫通.這就要求我們登高望遠，站在思想方法的高度進行復習教學，不僅要讓學生知道解題的方法、有幾種方法？更應讓學生了解這些方法有何聯系？是如何發現的？這樣才能有效提高復習的效率.如果說數學思想方法是根，那么解題方法就是葉，正所謂根深自然葉茂.

“函數與方程”是高三復習的核心內容與基本思想，一直受到高考命題專家的青睞，通過對這一思想方法的考查，可以檢測學生的思維能力、轉化能力、運算能力，從而實現知識向能力的轉化.對于此類問題的探究與考查，大多考查零點的個數及字母的取值范圍.（1）零點個數的考查主要是利用轉化思想，轉化為對應方程的根的個數或對應函數圖像與x軸的交點個數來研究；（2）字母取值范圍問題的考查主要是：①根據平移理論，結合零點個數平移直線，進而確定字母的范圍；②轉化為函數的值域來加以研究.因此，用“函數與方程思想”破解“函數零點與方程的根”，僅是數學思想方法論的一方面，還可通過數形結合思想、轉化思想去解決，或多種數學思想方法聯合應用.