探析二次方程根的分布問題高考命題視角

☉江蘇省丹陽高級中學 謝洪濤

教材是數學教育專家集體智慧的結晶，里面包含要求高中學生必須掌握的知識點及相關問題的解題思想方法，但受承載容量的限制，題型、方法的介紹不可能面面俱到，有一部分重要的題型和方法是以習題的形式體現的，因此對習題的拓展、探究就格外重要了.對習題的探究不僅可以對題型和方法進行歸納總結，而且還可以找到很多高考題的生長點.本文以一道二次方程根的分布的習題為例，就相關題型及解法進行探究.以期拋磚引玉.

題目（人教版必修5練習題）關于x的方程x2－（m+3）·x+m+3=0有兩個不相等的正實數根，求實數m的取值集合.

教材中并沒有對二次方程根的分布問題作系統的歸納，本文以此題為例，進行題型歸納及解題方法總結.

一、解法展示

解決此類問題可以從兩種視角入手.

解法1：（利用二次函數圖像）方程x2－（m+3）x+m+3=0有兩個不相等的正實數根，即二次函數f（x）=x2－（m+3）x+m+3與x軸正半軸有兩個不同交點.由二次項系數大于0知，二次函數f（x）的圖像開口向上，欲使其與x軸正半軸有兩個不同交點，則：

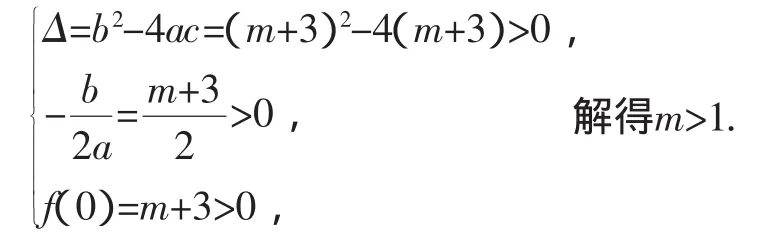
解法2：（利用根與系數的關系）方程x2－（m+3）x+m+3=0有兩個不相等的正實數根，即：

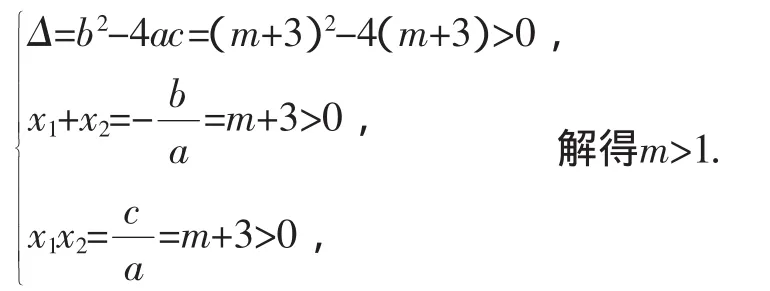
解題中根據不同的題型，兩種方法要擇優而用.

二、題型歸納

設一元二次方程ax2+bx+c=0（a＞0）的兩個實根為x1，x2，其根的分布問題除題目所示類型外，還有如下幾種類型.

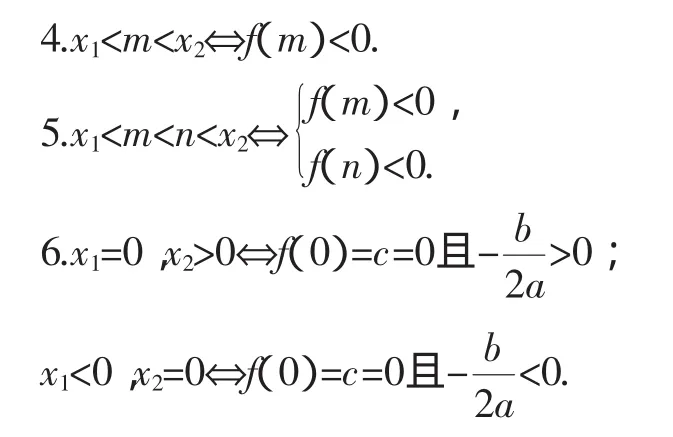
說明：在上述問題的解答中，若二次項系數的正負不確定，應就其可能取值情況進行分類討論.若二次項系數可能為0，則問題轉化為一次函數.

例1 若二次方程x2+（2m－3）x+4=0有且只有一個根在（0，1）內，求m的取值范圍.

解析：令f（x）=x2+（2m－3）x+4，由f（x）=0有且只有一個根在（0，1）內可知，

①f（0）f（1）＜0?4（2m+2）＜0?m＜－1；

綜上，m＜－1.

例2 若關于x的方程x2－x－m－1=0在［－1，1］上有兩個根，求m的取值范圍.

解析：令f（x）=x2－x－m－1，原問題轉化為以下兩種情況.

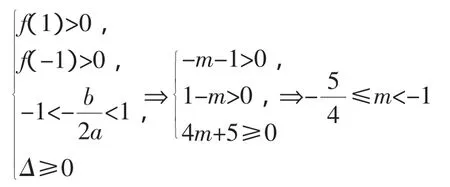
②f（1）f（－1）=0?m=±1.

當m=1時，原方程為x2－x－2=0?x1=－1，x2=2，不合題意；

當m=－1時，原方程為x2－x=0?x1=1，x2=0，合題意.

評析：在對上述兩題的解答中，除了注意零點個數的不同，還需要注意所給區間端點的變化對問題的影響.

三、高考命題視角

高考中對二次方程根的分布問題的考查多數都體現在利用導數求解函數的綜合題目中.解此類問題的基本策略是對函數求導后，在定義域內討論導數的正負，而導函數多為二次型或局部為二次型，進而將問題轉化為二次方程根的分布問題.

例3 （2015年山東理科）設函數f（x）=ln（x+1）+a（x2－x），其中a∈R.

（1）討論函數f（x）極值點的個數，并說明理由；

（2）若?x＞0，f（x）≥0成立，求a的取值范圍.

解析：（1）f（x）=ln（x+1）+a（x2－x），定義域為（－1，+∞）.

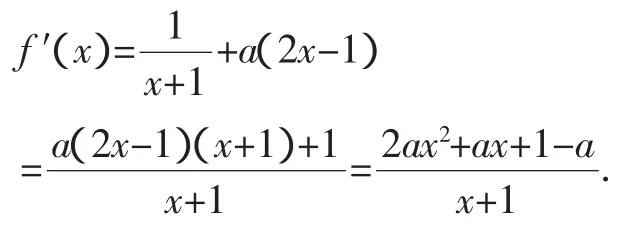
設g（x）=2ax2+ax+1－a，

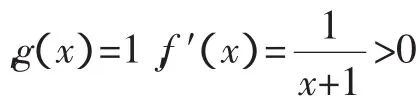
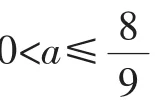
所以當x∈（－1，x1）時，g（x）＞0，f′（x）＞0，f（x）單調遞增；當x∈（x1，x2）時，g（x）＜0，f′（x）＜0，f（x）單調遞減；當x∈（x2，+∞）時，g（x）＞0，f′（x）＞0，f（x）單調遞增.

因此，此時函數f（x）有兩個極值點.

當a＜0時，Δ＞0，但g（－1）=1＞0，x1＜－1＜x2，所以當x∈（－1，x2）時，g（x）＞0，f′（x）＞0，f（x）單調遞増；當x∈（x2，+∞）時，g（x）＜0，f′（x）＜0，f（x）單調遞減.

所以函數只有一個極值點.

（2）略.

評析：本題在對函數求導、整理后決定導函數正負的是分子，分子為二次函數型，因此二次方程根的分布問題就登上了高考的舞臺.但二次項系數不確定，故應對其可能情況進行分類討論.

（1）若a＞0，函數y=f（x）在區間（a，a2－3）上存在極值，求a的取值范圍；

（2）若a＞2，求證：函數y=f（x）在（0，2）上恰有一個零點.

解析 ：（1）f′（x）=x2－2ax，令f′（x）=0，即f′（x）=x（x－2a）=0，所以x=0或x=2a.

因為a＞0，所以x=0不在區間（a，a2－3）內，要使函數在區間（a，a2－3）內存在極值，只需a＜2a＜a2－3，所以a＞3.

（2）略.

評析：函數在區間內存在極值點，即其導函數在區間內存在零點，求導后導函數為二次函數型，故問題轉化為二次方程根的分布問題.

解析：因為函數f（x）在區間（－1，1）不單調，所以函數f′（x）在（－1，1）上存在零點.而f′（x）=0的兩根為a－1，a+1，區間長為2，所以在區間（－1，1）上不可能有2個零點.所以f′（－1）f′（1）＜0，即a2（a+2）（a－2）＜0.

因為a2＞0，所以（a+2）（a－2）＜0，－2＜a＜2.

又因為a≠0，所以a∈（－2，0）∪（0，2）.

評析：本題從表面看，命題形式上有所變化，即函數在區間內不單調，但其本質仍是導函數在區間存在零點問題.通過挖掘隱含條件不難發現在區間內不可能存在兩個零點，故減少了分類討論的情況，優化了解題過程.

綜上所述，二次方程實根分布的理論，雖然直觀易懂，但在解決高考問題中的作用卻不可低估.它不但可以使相關問題的求解直觀簡潔，富有新意，而且對于培養學生運用函數與方程以及數形結合等思想方法解題的意識大有裨益.因此，在教學中，要注意引導學生重視對教材習題的探究、歸納、總結，進而提升學生對問題的分析、求解能力.