光伏系統模糊PSO的MPPT控制

李繼生，李金羽，游國棟，雷淑英

（天津科技大學電子信息與自動化學院，天津 300222）

光伏系統模糊PSO的MPPT控制

李繼生，李金羽，游國棟，雷淑英

（天津科技大學電子信息與自動化學院，天津 300222）

在局部陰影條件下，光伏陣列的功率-電壓特性曲線呈現多峰狀，傳統最大功率點跟蹤方法出現搜索精度低和收斂速度慢的問題.針對此問題提出一種基于模糊控制的粒子群優化算法，采用模糊控制器對粒子群優化算法的慣性權重ω進行優化，實時調整參數，使光伏陣列在光照強度變化時有較好的動態特性和穩態性能.分別采用常規PSO算法和模糊PSO算法在相同條件下對系統進行仿真，結果表明所提出的算法在局部陰影條件下能快速跟蹤外部環境變化，且準確地工作在最大功率點.

最大功率點跟蹤；局部陰影；粒子群優化算法；模糊控制

本文提出一種基于模糊控制的粒子群優化算法，對光伏陣列的最大功率點進行跟蹤控制，根據粒子群算法中參數的特點，采用模糊控制器優化粒子群算法的慣性權重ω，當光照強度發生變化時，能跟蹤控制并實時調整參數值，避免陷入局部最優值.最后采用常規粒子群優化算法和模糊粒子群優化算法對仿真模型進行對比分析.

1 光伏電池的建模

通常，太陽能光伏發電系統的電氣特性表示為功率對電壓（電流/占空比）和電流對電壓的比［10］.光伏電池的特性曲線呈非線性.圖1為光伏電池的等效電路.

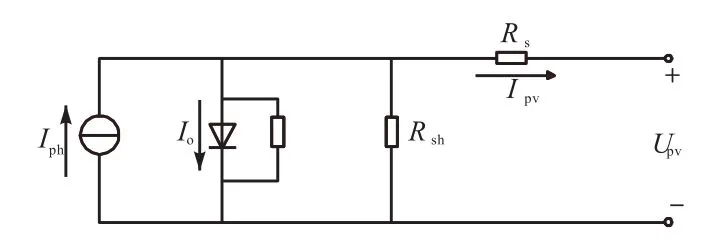
圖1 光伏電池的等效電路Fig. 1 Equivalent circuit of a PV array

光伏發電系統產生電流的數學模型為

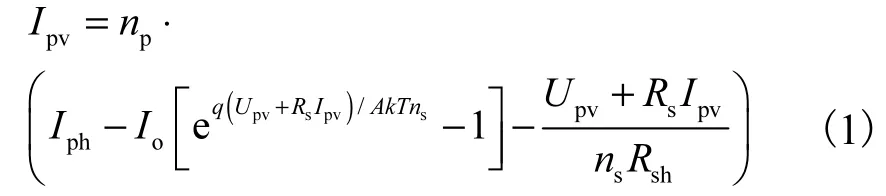
式中：Upv和Ipv分別為光伏輸出電壓和電流；Rs和分別為光伏電池的串聯和并聯電阻；q為電子電荷（1.6×10-19C）；Iph為光生電流；Io為二極管電流；A為光伏電池中半導體器件的P-N結系數；k為波爾茲曼常數（1.38×10-23J/K）；T為熱力學溫度；np和ns分別為光伏電池的串聯數目和并聯數目.

2 PSO算法在多峰MPPT中的應用

2.1 PSO算法

粒子群優化算法（PSO）是從鳥群覓食這一行為中推演產生的，它通過粒子群中各個粒子的不斷迭代、更新來找尋最優解［11］.粒子根據其追隨的2個“最優值”使個體得到更新.其中一個“最優值”指粒子從初始至當前時刻內的最好位置，即個體最優值（Pbest），另一個“最優值”是種群里全部粒子至當前時刻為止找到的最好位置，即全局最優值（Gbest）.第t+1次迭代時，第i個粒子的速度及位置通過式（2）和式（3）更新.

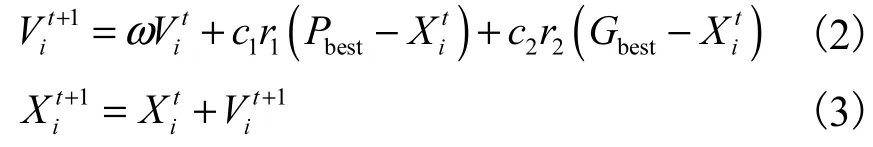
式中：t為迭代次數；ω為慣性權重；c1和c2為學習因子；1r和r2為［0，1］上的隨機數.

2.2 PSO算法在多峰MPPT中的應用

當光伏電池所受光照強度均勻時，光伏電池的P-U、I-U特性曲線呈單峰狀；當光伏電池所受光照強度不均勻，即存在局部陰影情況時，P-U、I-U特性曲線呈多峰狀，這種情況下很容易產生誤判，將追蹤到的局部極值點當成全局極值點［12］.局部陰影下光伏陣列的輸出特性見圖2.其中，曲線a和曲線b分別表示光照強度均勻和不均勻時的特性曲線.

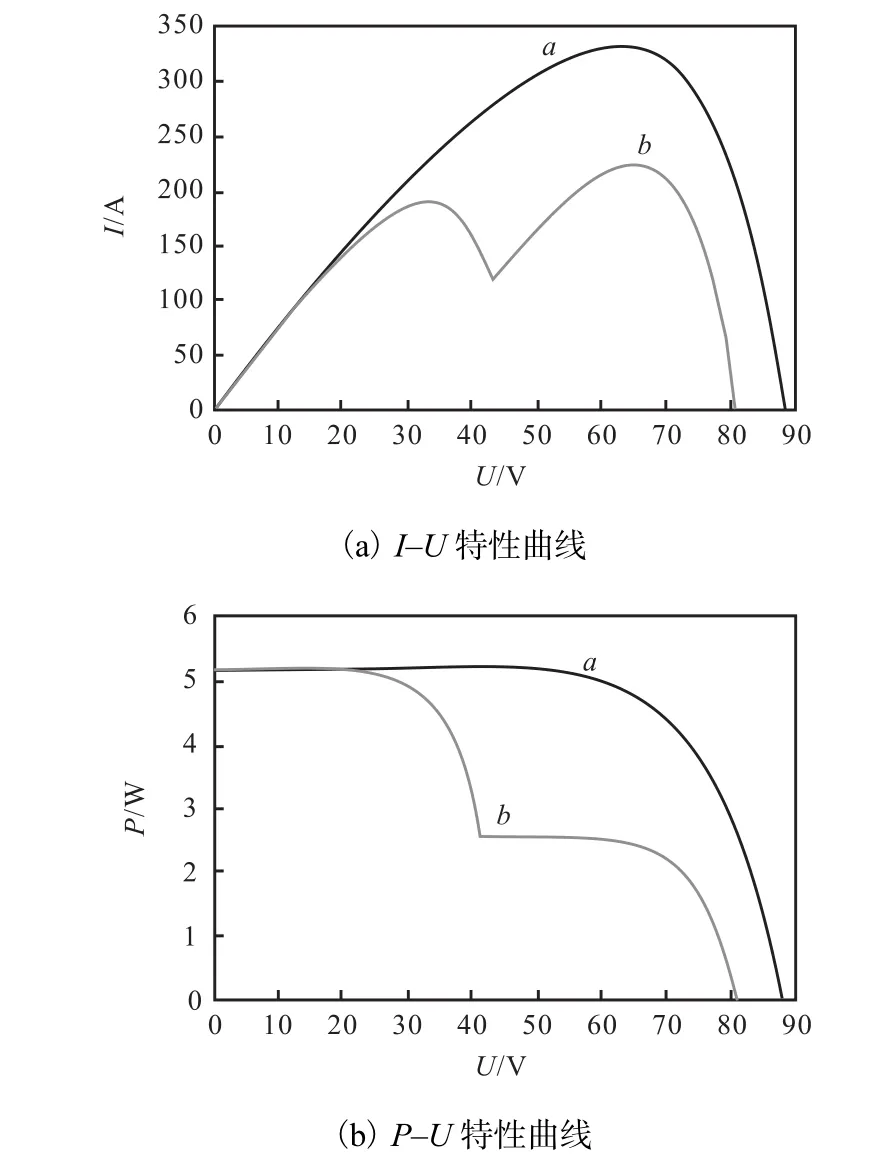
圖2 局部陰影下光伏陣列的輸出特性Fig. 2Output characteristics of the PV array under partial shade

在局部陰影條件下，采用粒子群優化算法進行最大功率點跟蹤時，需要對粒子群的參數進行初始化，以往對參數的設置基本上是依據經驗.文獻［11］指出，粒子的維數是取決于與其相關的優化問題；粒子的最大速度決定當前時刻位置與最優值間區域的分辨率；學習因子取值過小或過大，都會導致粒子遠離目標區域.本文參考現有文獻資料，并結合實驗，設置PSO算法的參數為：粒子總數N=100，粒子初始速度V0=0，最大速度限定值Vmax=2，學習因子c1==2，慣性權重ω=0.4.選擇光伏陣列輸出總功率函數作為適應函數.由式（2）、式（3）可知，每次迭代時，粒子的速度和位置會更新.

2.3 特性分析

為準確且快速地獲得全局最優解，粒子群優化算法的參數設置至關重要，而慣性權重ω又在參數中占據主要地位，它決定粒子的此次迭代速度對下次迭代速度的影響程度.在算法中，若慣性權重保持恒定不變，則無法保證局部搜索與全局搜索之間的平衡.慣性權重過小或過大也會對算法造成不利影響：慣性權重過小，雖然能提高算法的局部搜索能力，但會延長收斂時間，容易陷入局部最優值；慣性權重過大，會導致精確解的搜索變困難，難以獲得全局最優值［13］.只有當慣性權重取值恰當時，才能既避免陷入局部最優值，又快速獲得精確解.

3 基于模糊控制的粒子群優化算法MPPT

本文將模糊控制器加入到粒子群算法中，采用模糊控制來調整粒子群慣性權重ω，避免粒子陷入局部最優值［14-15］.在充分考慮粒子群個體分布、進化程度及最優適應度對慣性權重的影響后，建立相應的模糊規則，通過計算最近3次迭代中粒子的平均適應度值，優化慣性權重ω.

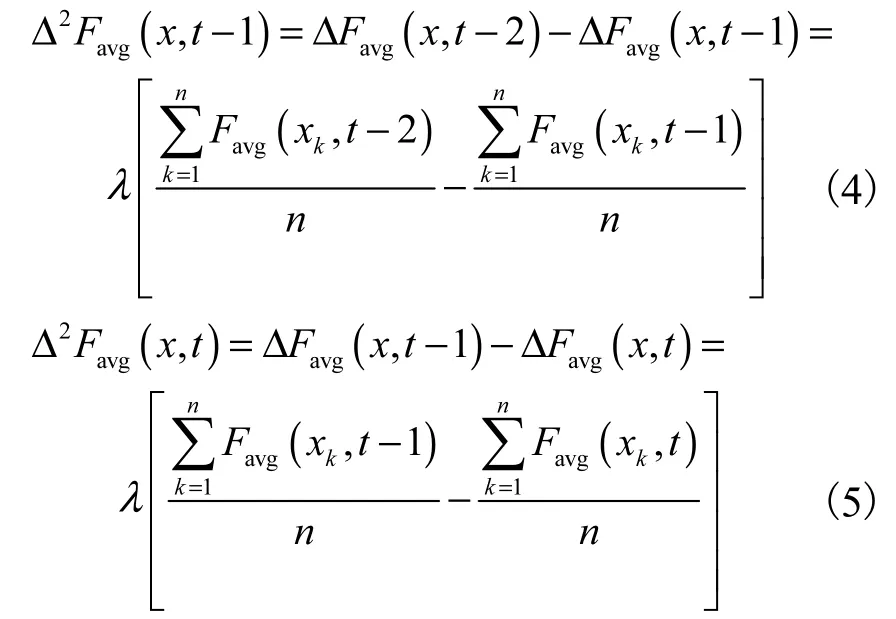
按照以下規則判斷并調整參數ω：

其中，ε為給定的趨近于零的正實數；γω為隸屬函數的最大值（本文中γω=1）.

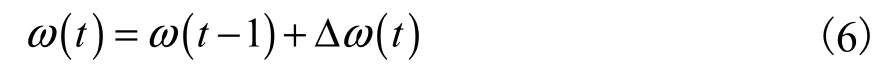
模糊控制器包括模糊化、模糊推理和解模糊3個部分，它將輸入量模糊化，采用模糊規則進行模糊推理，最后通過反模糊化，使輸出量精確化.模糊控制器框圖如圖3所示.

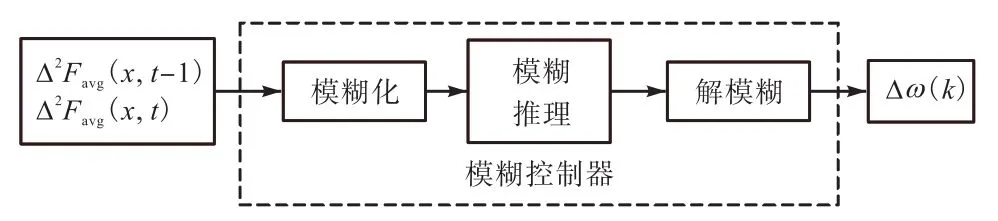
圖3 模糊控制器框圖Fig. 3 Diagram of the fuzzy controller

輸入量和輸出量均離散化為11級，分別標準化到［-1，1］和［-0.1，0.1］；模糊子集均為｛NB，NL，NM，NS，ZE，PS，PM，PL，PB｝，即｛負大，負較大，負中，負小，零，正小，正中，正較大，正大｝.輸入量和輸出量隸屬度函數分別如圖4、圖5所示.

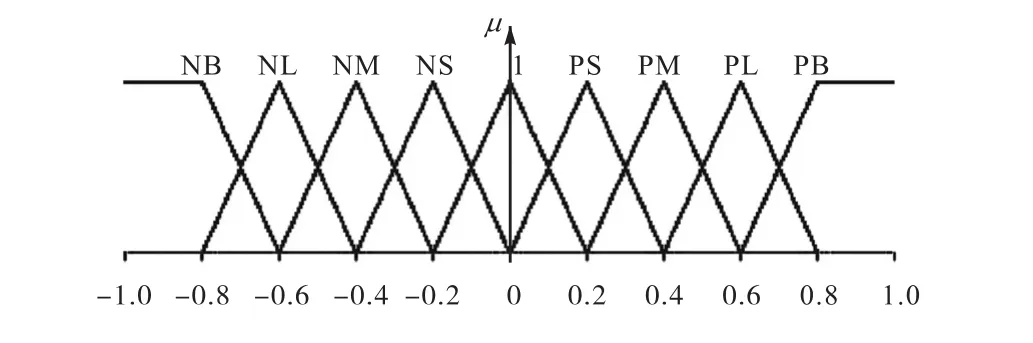
圖4 輸入量Δ2（x，t -1）和Δ2（x，t ）的隸屬度函數Fig. 4 Member functions of Δ2（x，t -1）and Δ2（x，t ）

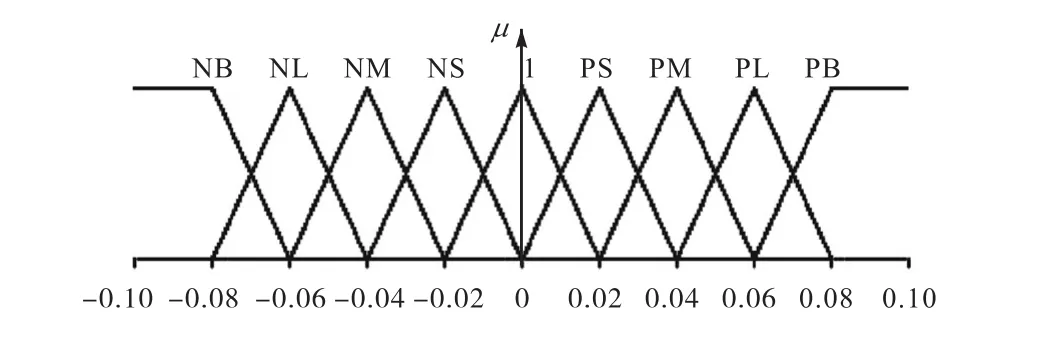
圖5 輸出量Δω的隸屬度函數Fig. 5 Member function of Δω

根據粒子群算法特點、參數特性及其對算法的影響，制定模糊控制規則和反模糊化表.模糊控制規則共81條，見表1.

表1 的模糊控制規則Tab. 1 Fuzzy control rules for

表1 的模糊控制規則Tab. 1 Fuzzy control rules for

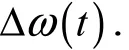
表2 反模糊對應值的規則表Tab. 2 Defuzzification control rules for

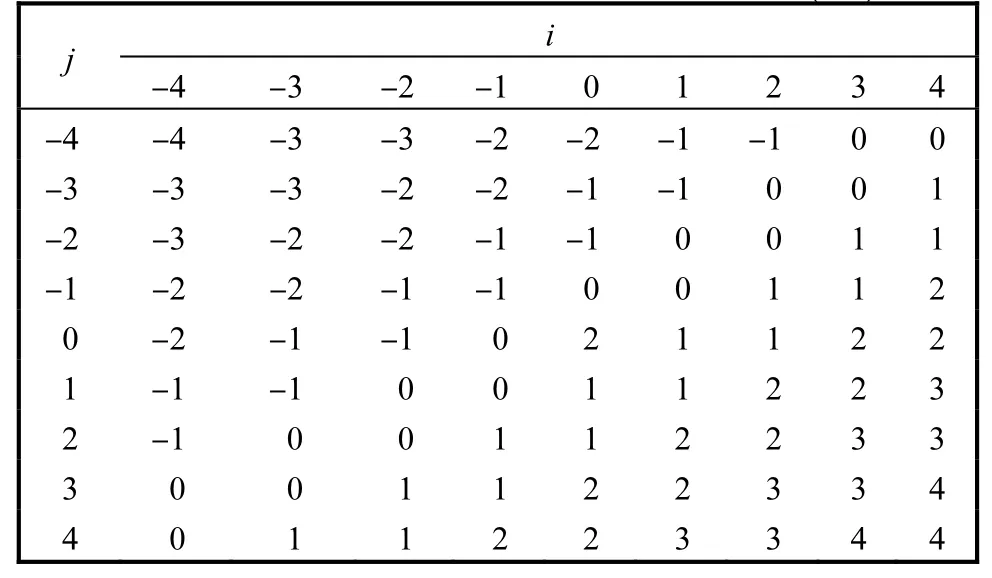
表2 反模糊對應值的規則表Tab. 2 Defuzzification control rules for

?

算法的實現步驟如下：

（1）根據設定算法的各個參數，對粒子的位置及速度進行初始化；

（2）根據適應函數計算各粒子的適應值，確定個體歷史最優值Pbest和全局最優值Gbest；

（5）按照式（2）、式（3）更新各粒子的速度及位置，根據函數判斷當前粒子個體歷史最優值、粒子群是否處在全局最優值，更新Pbest和Gbest；

（6）判斷是否滿足終止條件，若滿足則輸出結果并結束算法，否則返回步驟（3），繼續執行.

4 仿 真

根據本文提出的改進的粒子群優化算法，采用Matlab/Simulink對10個額定功率為850，W的系列模塊進行仿真，仿真模型如圖6所示.設置光伏模塊的參數為：輸出電壓300，V，升壓電感0.3，H，濾波電容2，200，μF，開關頻率4，kHz.

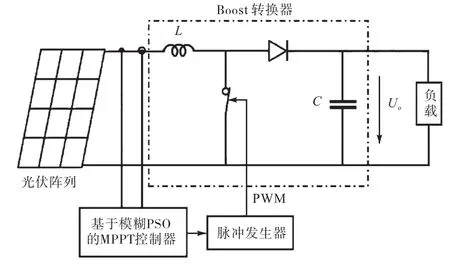
圖6 基于模糊PSO的仿真模型Fig. 6 Simulation model based on fuzzy PSO

局部陰影條件下，為了比較常規PSO與模糊PSO（MPPT）的性能，在相同條件下對兩種方法進行仿真，采用不同的分布式輻射水平進行測試：7個非陰影模塊接收的輻射為1，000，W/m2，另外3個部分陰影模塊接收的輻射水平分別為800、500和100，W/m2.光伏陣列的輸出功率如圖7所示.

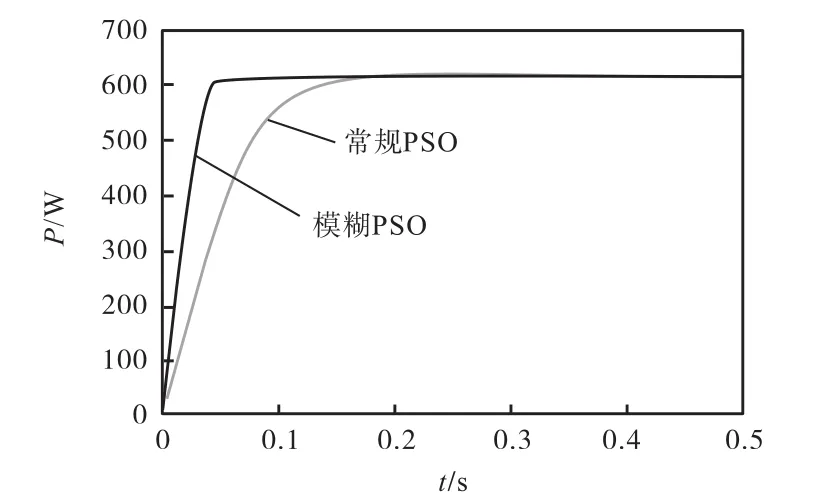
圖7 局部陰影條件下光伏系統的動態響應Fig. 7Dynamic response of the PV system under partially shaded conditions

由圖7可以看出，局部陰影條件下，常規PSO算法與模糊PSO算法均能跟蹤到最大功率點.常規PSO算法在整個MPPT跟蹤過程中功率波動較大，跟蹤速度較慢，而模糊PSO的全局極值點跟蹤速度較快，振蕩幅度較小，穩態精度較高.

為進一步驗證該方法，對非陰影模塊使用具有不同輻射水平的相同的局部陰影條件.輻射水平在0.5，s內從500，W/m2變化至1，000，W/m2，再在1，s內從1，000，W/m2變化至500，W/m2.結果見圖8.可以看出：即使是在變化的天氣條件下，MPPT也能在較短時間內掃描并跟蹤全局極值點；在光照強度發生劇烈變化的情況下，與常規PSO相比，采用模糊PSO的系統到達穩定所需的時間更短，波形畸變更小，具備良好的跟蹤性能.

5 結 語

本文提出了一種基于模糊控制的粒子群優化算法，用于跟蹤控制局部陰影下光伏陣列的最大功率點.將模糊控制器加入到粒子群優化算法中，優化粒子群算法中的參數ω，建立光伏陣列數學模型，并在局部陰影條件下進行仿真研究.通過仿真分析可以看出：與傳統粒子群算法相比，模糊粒子群算法的跟蹤速度更快，穩態精度更高；本文提出的算法在不同陰影條件及陰影條件變化時均能有效追蹤到最大功率點，并能有效減少采用常規PSO時在最大功率點附近的振蕩幅度.

［1］ 周林，武劍，栗秋華，等. 光伏陣列最大功率點跟蹤控制方法綜述［J］. 高電壓技術，2008，34（6）：1145-1154.

［2］ 楊水濤，張帆，丁新平，等. 基于輸入-輸出參數的光伏電池最大功率控制的比較［J］. 電工技術學報，2009，24（6）：95-102.

［3］ 吳理博，趙爭鳴，劉建政，等. 單級式光伏并網逆變系統中的最大功率點跟蹤算法穩定性研究［J］. 中國電機工程學報，2006，26（6）：73-77.

［4］ 劉曉艷，祁新梅，鄭壽森，等. 局部陰影條件下光伏陣列的建模與分析［J］. 電網技術，2010，34（11）：192-197.

［5］ 肖景良，徐政，林崇，等. 局部陰影條件下光伏陣列的優化設計［J］. 中國電機工程學報，2009，29（11）：119-124.

［6］ 朱艷偉，石新春，但揚清，等. 粒子群優化算法在光伏陣列多峰最大功率點跟蹤中的應用［J］. 中國電機工程學報，2012，32（4）：42-48.

［7］ Noguchi T，Togashi S，Nakamoto R. Short-current pulsebased adaptive maximum-power-point tracking for a photovoltaic power generation system［J］. Electrical Engineering in Japan，2002，139（1）：65-72.

［8］ Kobayashi K，Takano I，Sawada Y. A study of a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions［J］. Solar Energy Materials and Solar Cells，2006，90（18）：2975-2988.

［9］ Miyatake M，Toriumi F，Endo T，et al. A novel maximum power point tracker controlling several converters connected to photovoltaic arrays with particle swarm optimization technique［C］//2007 European Conference on Power Electronics and Applications. Piscataway：IEEE，2007：1-8.

［10］ Alajmi B N，Ahmed K H，Finney S J，et al. A maximum power point tracking technique for partially shaded photovoltaic systems in microgrids［J］. IEEE Transactions on Industrial Electronics，2013，60（4）：1596-1606.

［11］ 吳海濤，孫以澤，婥孟. 粒子群優化模糊控制器在光伏發電系統最大功率跟蹤中的應用［J］. 中國電機工程學報，2011，31（6）：52-57.

［12］ Gen M，Yun Y S. Soft computing approach for reliability optimization：State-of-the-art survey［J］. Reliability Engineering & System Safety，2006，91（9）：1008-1026.

［13］ 趙陽，符強，王鐳，等. 基于粒子群算法的最大功率點跟蹤方法研究［J］. 電力電子技術，2010，44（6）：32-33.

［14］ 劉琳，陶順，鄭建輝，等. 基于最優梯度的滯環比較光伏最大功率點跟蹤算法［J］. 電網技術，2012，36（8）：56-61.

［15］ 任海鵬，郭鑫，彧楊，等. 光伏陣列最大功率跟蹤變論域模糊控制［J］. 電工技術學報，2013，28（8）：13-19.

責任編輯：常濤

MPPT Control of PV System Based on Fuzzy PSO Algorithm

LI Jisheng，LI Jinyu，YOU Guodong，LEI Shuying
（College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China）

Under partially shaded conditions，multiple local maximum can be exhibited on the power-voltage characteristic curve. To solve the problem of the low rate of searching precision and convergence using conventional maximum power point tracking methods，a control algorithm based on Particle Swarm Optimization algorithm using fuzzy control was proposed. Fuzzy controller was used to optimize the inertia weightωof PSO algorithm to ensure that the system has better dynamic response speed and steady-state accuracy when solar radiation changes. Simulation was performed with the PSO method and Fuzzy PSO method under the same condition，and the results indicate that the proposed global MPPT algorithm can quickly and accurately track the global maximum under partially shaded conditions.

maximum power point tracking（MPPT）；partially shaded conditions；particle swarm optimization（PSO）algorithm；fuzzy control

TM914 文獻標志碼：A 文章編號：1672-6510（2015）01-0073-05

10.13364/j.issn.1672-6510.20140086

由于傳統能源和環境問題的限制，清潔可再生能源越來越受到國內外研究者的關注.太陽能因其分布廣、無污染等優點而具有良好的應用前景［1-3］.研究者通常采用最大功率點跟蹤（maximum power point tracking，MPPT）技術提高光伏電池的利用率.然而，光伏系統的輸出電壓和電流之間存在非線性關系，且在局部陰影條件下，系統的P-U特性曲線有多個峰值，易發生誤判［4-6］.

2002年，Noguchi等［7］提出一種基于短路脈沖的MPPT算法，可快速掃描P-U特性曲線來確定比例參數，找到全局極值點，但該方法會引起瞬時功率的損耗.2003年，Kobayashi等［8］設計了一個使用監控單元的兩級MPPT，在第1階段，當P-U特性曲線均勻時，它的工作點移動到最大功率點；在第2階段，采用增量電阻法來定位實際的最大功率點，但該方法在局部陰影情況下可能會陷入局部極值點.2007年，Miyatake等［9］在光伏陣列中應用粒子群優化算法，它易于實現，搜索速度較快，但是其參數通常依據經驗設置，缺乏固定的參考模型，對算法的收斂性及穩定性也缺乏嚴謹的數學分析.因此，考慮將粒子群優化算法與其他控制方法相結合，彌補粒子群優化算法的局限性，進而提高系統精度.

2014-05-29；

2014-09-05

天津市自然科學基金重點資助項目（13JCZDJC29100）

李繼生（1963—），男，遼寧錦州人，教授，lijish@tust.edu.cn.