行星運動中曲率半徑的分析

王璐珠

（湖南師大附中，湖南 長沙 410006）

1 問題的提出

人造地球衛星沿橢圓形軌道繞地球運行，近地點A到地球中心C的距離為r1，遠地點B到地球中心的距離為r2，衛星在近地點A處的速率為vA，衛星在遠地點B處的速度vB多大？

學生：利用萬有引力提供向心力，

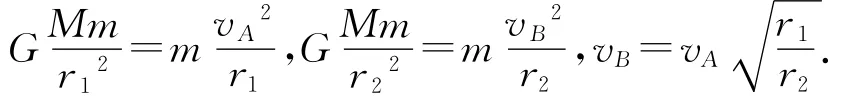
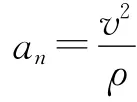
2 橢圓曲率半徑的分析

思路1.（根據物理表達式分析計算）：［1］圖1所示的橢圓，數學參量方程為x＝acosφ，y＝bsinφ，設質點以φ＝ωt的方式沿橢圓軌道運動，其中ω為常量，聯系簡諧運動知識，可得

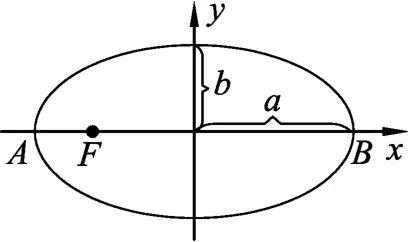
圖1

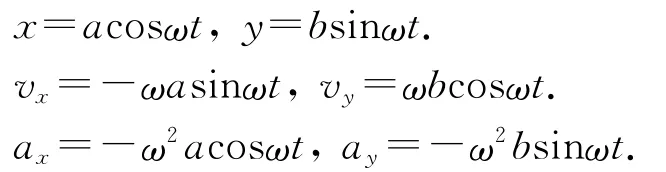
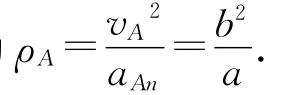
思路2.（根據對稱思想定性分析）：曲線上各點的彎曲程度不同，則曲率半徑也就不同，并且彎曲程度大的曲率半徑越小，反之亦反.但由于橢圓軌道上的長軸兩端點處對稱，則曲率半徑相等，可都用ρ來表示.

當學生有了正確的思路后，解法便呈現了多樣性，以下是不同學生對此題的正解.

3 正確的求解

解法1.（萬有引力提供向心力）

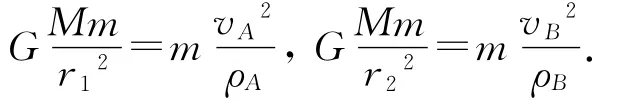
根據以上思路易證得

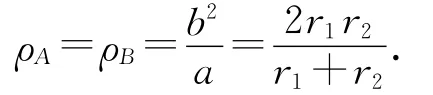
解法2.（開普勒第二定律）

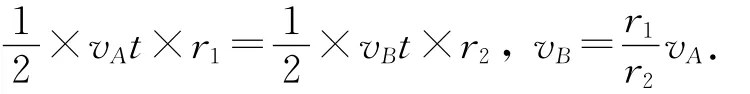
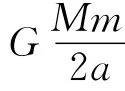
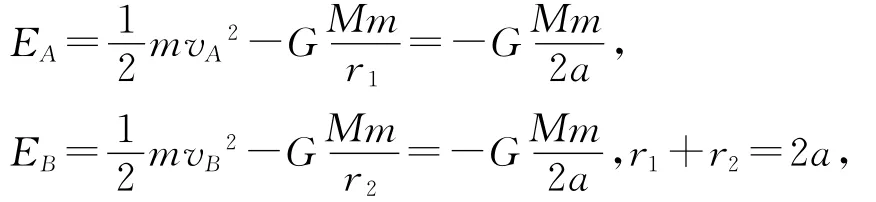
學生的潛力是無限的，正向引導和開發便可找到物理世界無盡的奧妙所在.借用此題他們很快找到解決另一道類題的方法.

4 習題拓展

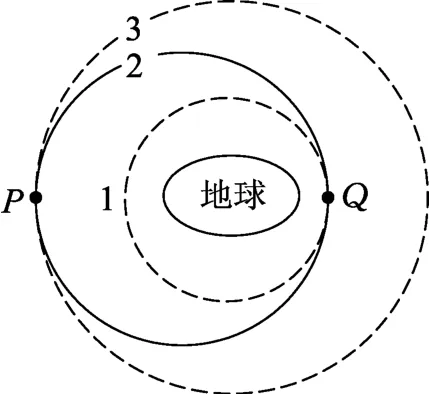
圖2

發射地球同步衛星時，先將衛星發射至近地圓軌道1，然后經點火，使其沿橢圓軌道2運行，最后再次點火，將衛星送入同步圓軌道3，如圖2，則衛星分別在1、2、3軌道上正常運行時：

（1）衛星在軌道1上經過Q點的加速度與衛星在軌道2上經過Q點加速度的大小關系.

（2）衛星在軌道1、2上經過Q的速度分別為v1、v2，衛星在軌道2、3上經過P的速度分別為v3、v4，比較這4個速度的大小.

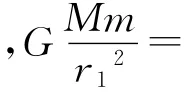
可見，在曲線運動教學中應根據學生情況適當補充曲率圓、曲率半徑的知識，并予以一定的定量分析，讓其正確理解物理概念，理性分析物理情境，熟練運用物理公式，便可走出思維定勢，消除“負遷移”的影響.

1 舒幼生.數學曲率半徑的運動學解［J］.物理教學，2004：4－6.