高頻地波雷達飛行目標高度屬性判別

趙孔瑞，于長軍，劉愛軍，菅維樂，權太范

（1.哈爾濱工業大學電子與信息工程學院，黑龍江哈爾濱150001；2.哈爾濱工業大學（威海）信息與電氣工程學院，山東威海264200）

高頻地波雷達飛行目標高度屬性判別

趙孔瑞1，于長軍2，劉愛軍2，菅維樂2，權太范2

（1.哈爾濱工業大學電子與信息工程學院，黑龍江哈爾濱150001；2.哈爾濱工業大學（威海）信息與電氣工程學院，山東威海264200）

高頻地波雷達飛行目標高度估計一直是工程上尚未解決的熱點問題。然而在實際工程應用中，更加關心的是被探測到的飛行目標是高空還是低空的高度屬性問題，而且飛行目標高度屬性判別研究比精確估計目標的具體飛行高度更有實際應用意義，且更容易在實際系統中實現。基于上述工程設計思想，提出高頻地波雷達飛行目標高／低屬性判別工程化方法，首次解決了高頻地波雷達飛行目標高度屬性判別問題。所提方法利用垂直極化電波在高空和低空高度區域的不同電波傳播衰減特性構建高度屬性判別算法，不僅判別目標高度屬性，而且給出高度屬性判別可信度。實測數據處理表明，所提方法能夠利用少量觀測數據快速判別飛行目標高度屬性，可信度達到90%以上。

高頻地波雷達；高度屬性；電波傳播衰減

0 引 言

高頻地波雷達（high frequency surface wave radar，HFSWR）發射垂直極化電磁波沿海面傳播衰減較小的特點，能夠探測數百公里外的海上飛行目標［14］，為海監部門打擊海上走私、海上交通管制、專屬經濟區保護提供了新途徑和手段［5-7］。HFSWR利用電波傳播繞射機理可以探測到超視距飛行目標，同時由于HFSWR垂直波束較寬，還可以探測到高空視距目標。但是，目前HFSWR只能獲取目標的距離和方位信息，不能直接獲取飛行目標的高度信息，因而無法判別目標高度屬性，即無法判別是高空目標還是低空目標。正如文獻［8］所指出的那樣“這種雷達不能立即區別在視線范圍內位于同一超過地平線距離上而有不同高度的目標”。

為判別飛行目標的高／低空屬性，可以利用傳統方法先精確估計目標飛行高度再判別目標飛行高度屬性。但是目前HFSWR都是利用斜距和方位信息估計高空目標的飛行高度，這些方法不能適用于低空飛行目標高度估計問題。文獻［9］利用HFSWR信號回波強度提出了一種目標高度和目標散射截面積（radar cross section，RCS）的實時估計方法。但是這種方法在高度估計時是一個多解問題，高度估計誤差較大，高度估計結果可信度低。雖然基于上述方法提出了許多改進算法，但仍然沒有從根本上解決高度估計的多解問題［10-12］，至今無法應用于HFSWR實際系統中。從工程應用角度看，HFSWR飛行目標高度估計仍處于探索階段。在HFSWR海上飛行目標預警應用中，往往更關心目標是低空飛行狀態還是高空飛行狀態。能夠直接、快速判別飛行目標是高空還是低空屬性，即獲取飛行目標高度屬性比精確估計目標的具體飛行高度更有實際應用意義，而且更容易在實際HFSWR系統上實現，也從而回答文獻［8］提出的HFSWR探測飛行目標無高度判別的問題。

基于上述工程設計思想，本文重點解決HFSWR飛行目標低空／高空屬性判別問題。利用垂直極化電波在高空和低空高度范圍內的不同傳播衰減特性提出一種目標高度屬性判別算法，而不估計目標具體飛行高度。這種方法不僅判別目標高度屬性，而且還給出高度屬性判別可信度。最后通過實測數據對本文提出的方法進行驗證。

1 HFSWR傳播衰減

根據單基地HFSWR方程可以得到接收站信號回波強度為

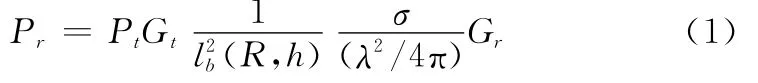
式中，Pr為接收信號回波強度；Pt為發射站信號發射功率；Gt為發射天線增益；Gr為接收天線增益；σ為目標RCS；h為目標高度；R為目標距離雷達觀測站的距離；lb（·）表示國際電信聯盟采用的地波傳播衰減，其是目標飛行高度h和目標距離R的函數；λ表示發射站雷達工作頻率。

將雷達方程式（1）取對數，可得分貝形式下的表示形式為

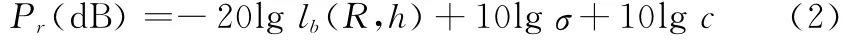
令

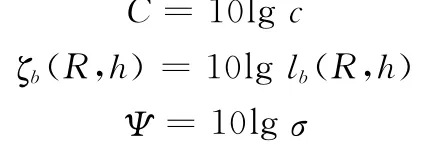
那么，式（2）表示為

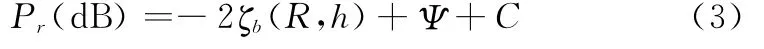
由HFSWR方程式（3）可知，假設雷達系統參數恒定，那么C也是已知的。目標回波強度Pr是傳播衰減ζb（R，h）和飛行目標RCSΨ的二元函數。將信號回波強度看作一個已知的常量，目標RCS和電波傳播衰減之間具有線性約束關系。此外，電波傳播衰減ζb（R，h）是目標距離和飛行高度的函數。因此，要實現目標飛行高度屬性判別，需要分析垂直極化電波傳播在不同高度上的傳播衰減特性。

在高頻波段，Rotheram模型考慮了大氣的折射指數，并對傳播衰減模型進行了詳細的理論推導，其傳播衰減曲線被國際電信聯盟采納為10 k Hz～30 MHz的地波傳播衰減標準［13-14］。因此，基于Rotheram傳播衰減模型的獨特優勢，本研究中采用Rotheram傳播衰減模型計算不同高度和距離上的傳播衰減曲線。首先，根據Rotheram模型給出一個傳播衰減的例子。在雷達工作頻率10 MHz，發射站高20 m，雷達站和目標之間距離為40～140 km的范圍內，目標飛行高度分別在高空區域和低空區域可以得到傳播衰減曲線如圖1和圖2所示。

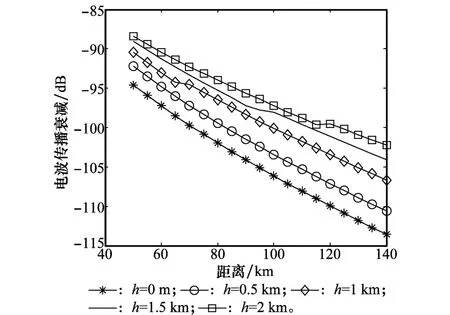
圖1 低空域地波傳播衰減

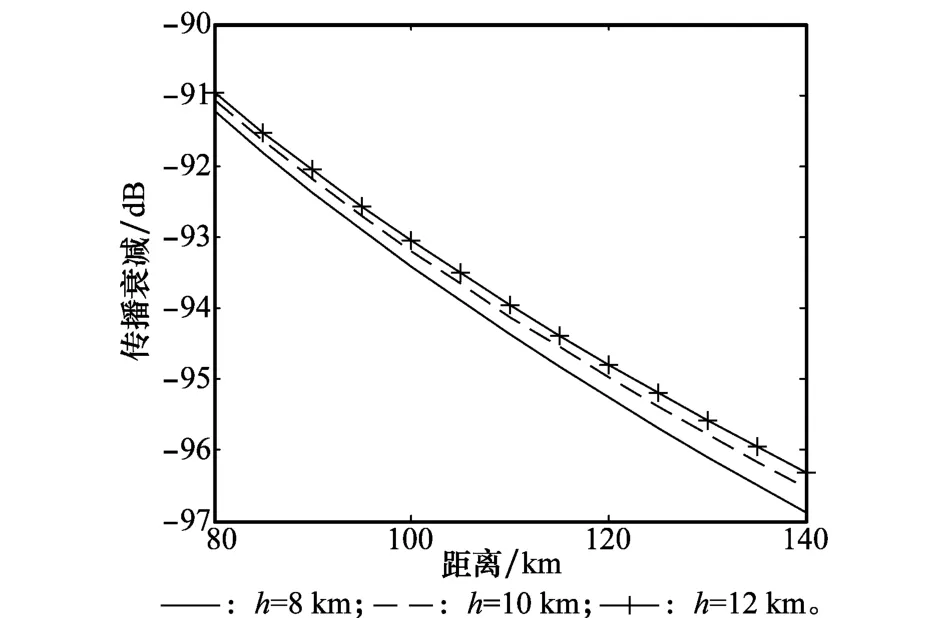
圖2 高空域地波傳播衰減

由圖1和圖2可見，地波傳播衰減曲線在不同高度上都隨著距離的增大而增大；在高度方向上隨著高度的增加，衰減逐漸減小。此外，由圖1可見，當飛行高度低于2 km時，不同高度上的衰減曲線區分比較明顯，高度變化0.5 km時可以引起2 dB的偏差。而在高空空域，由圖2可見，隨著高度的增大，在不同高度上的傳播衰減差別越來越小，即使從8 km增大到12 km，在距離140 km處的傳播衰減僅僅減小0.58 dB；當目標距離更近時，傳播衰減差別越不明顯。例如，目標距離為80 km時，傳播衰減之差僅僅為0.26 d B。由此可見，在高空區域傳播衰減區別不明顯。這是因為隨著高度的增加，海面效應對電波傳播衰減的影響越來越小，垂直極化電波衰減越來越近似于大氣傳播衰減。因此，垂直極化電波傳播衰減在高空和低空區域的不同傳播衰減特性為目標飛行高度屬性判別提供了可能。

2 高度屬性判別算法

為簡化問題分析，假定目標具有兩種高度屬性：低空屬性和高空屬性，分別用Dh和Dl表示。同時假設感興趣的低空范圍為0～2 km，高空范圍為7～12 km。由垂直極化電波傳播衰減特性可知，目標飛行高度較高時，高度信息對信號回波強度的影響很小，可以忽略高度對信號回波強度的影響。因此，用目標高度為10 km處的傳播衰減代替高空區域內任意高度上的傳播衰減。那么，式（3）可以重新定義為

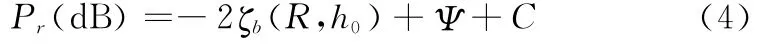
式中，h0＝10 km。

定義目標狀態向量為

式中，Ψ為目標相對于觀測站的RCS大小；vΨ為目標RCS變化率。假定飛行目標相對觀測站的姿態角是慢變化的，那么目標RCS也是慢變化的。則定義目標狀態方程為

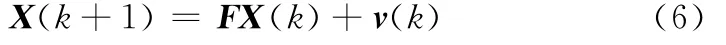
式中，F∈R2×2為狀態轉移矩陣；v（k）為零均值、白高斯過程噪聲。

由信號回波強度可定義量測值為

式中，H∈R1×2是量測矩陣；H＝［1 0］。式（6）和式（7）構成了高空飛行狀態下的目標高度屬性判別模型。

目標在低空飛行狀態下，由海面作用引起的地波傳播附加衰減影響較大，即使在目標飛行高度上升0.5 km的情況下，傳播衰減將減小2 dB以上。因此，假定在2 km以下的區域為低空區域，將高度0～2 km的范圍劃分為4個高度子空間，高度劃分節點分別為h1＝0.5 km，h2＝1 km，h3＝1.5 km。在每個高度節點上分別建立高度屬性判別模型。即每個高度子區間的屬性判別量測模型為

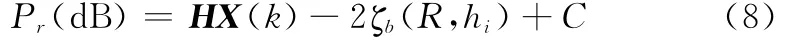
式中，i＝1，2，3。

因此，為實現目標高度屬性判別，可以在每個高度屬性區間利用式（8）建立相應的判別模型，其中，h0表示高空屬性；hi（i＝1，2，3）表示低空屬性。然后利用多假設思想，在每個高度區間上分別建立獨立的狀態估計模型，此處的狀態估計模型重點不是估計目標狀態信息，而是利用每個模式下的狀態估計信息來求解每個高度屬性判別的可信度，依據可信度的大小對目標飛行高度屬性進行判別，而不必考慮狀態估計精度。定義高度屬性可信度如下：

（1）高空屬性可信度

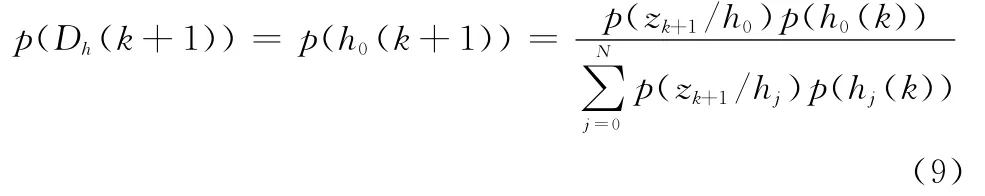
（2）低空屬性可信度

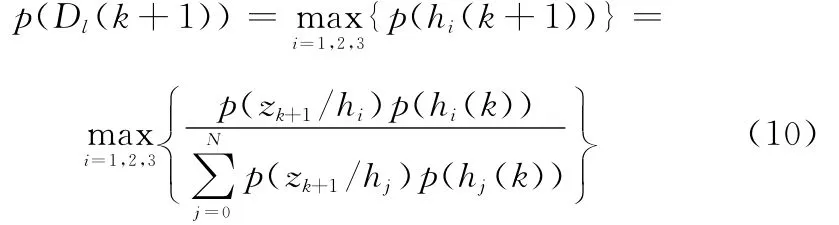
式中，N＝3；p（hi（k））（i＝1，2，3）為第i個高度區間模型的概率大小；p（zk+1／hi）為k+1時刻目標處于hi高度區間時的量測似然函數。假設量測噪聲為零均值高斯白噪聲，量測似然函數p（zk+1／hi）可以表示為

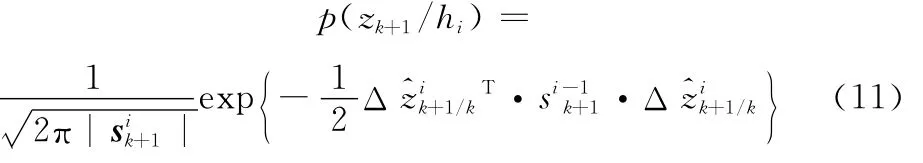
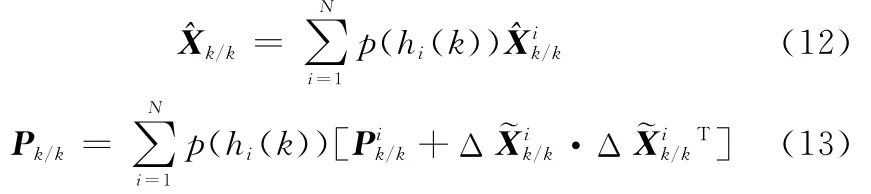
3 實測數據驗證

為驗證高度屬性判別算法的有效性，利用實測數據對其進行驗證。雷達工作頻率為11.4 MHz，發射功率為1 k W。飛行目標相對于高頻地波雷達站的飛行航跡如圖3所示，目標飛行高度為200 m，相對于雷達觀測站方位角為14°。高度屬性判別如圖4所示。

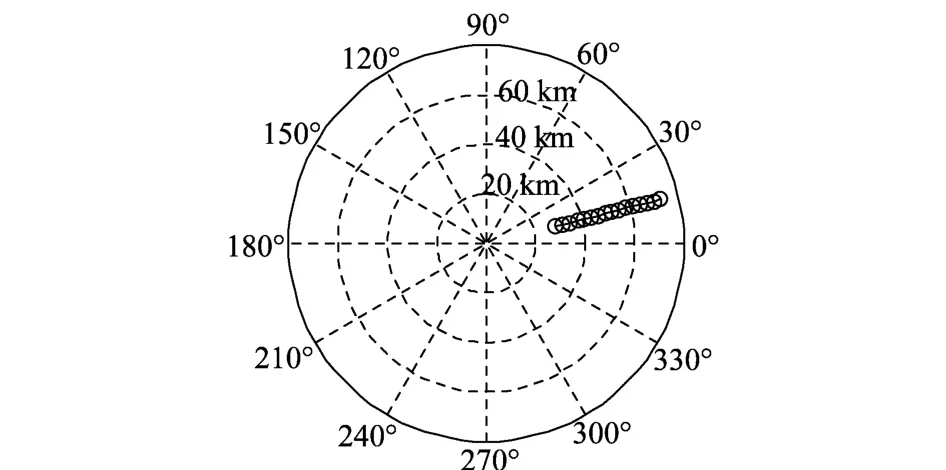
圖3 目標相對于觀測站航跡

圖4 目標低空屬性可信度

由圖4可見，本文提出的高度屬性判別算法可以準確地判別低空飛行目標的高度屬性。判別速度較快，只需要3個量測點跡信息就可以對目標高度屬性進行正確判別，且目標高度屬性判別可信度為1。

第2批次低空目標飛行高度為900 m，相對于觀測站的方位角為14.8°。目標相對于觀測站的航跡如圖5所示，高度屬性判別結果如圖6所示。

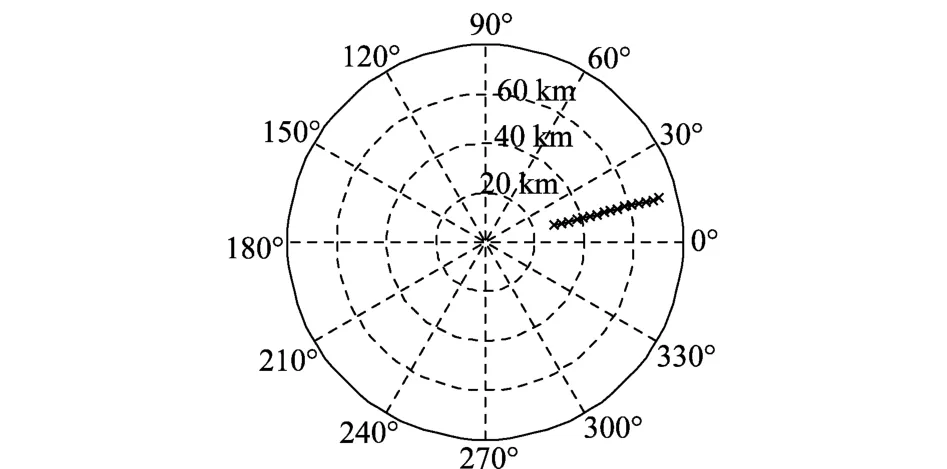
圖5 目標相對于觀測站航跡

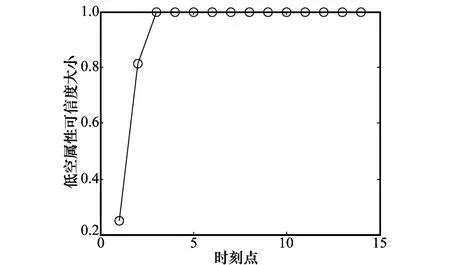
圖6 目標低空屬性可信度大小

由圖6可見，在目標飛行高度為900 m的情況下，在4個量測點跡時間內仍然可以正確判別出目標高度屬性，判別速度快。

以上分析了低空目標的高度屬性判別，并得到了精確的判別結果。以下部分將驗證高空飛行目標的飛行高度屬性判別，該目標為非合作民航目標，高度信息未知，采用文獻［10］提出的方法估計目標高度。

第3批飛行目標為高空飛行民航目標，其相對于雷達觀測站的航跡如圖7所示，目標飛行高度估計和高度屬性判別可信度分別如圖8和圖9所示。該民航目標飛往韓國、日本方向，目標高度估計高度為11 km，航向速度為938.9 km／h。一般國際民航飛機飛行高度為10.7 km左右，高度估計結果為11 km與經驗值相符合，且高空屬性判別可信度達到0.95左右。因此，以上飛行高度和屬性判別結果驗證了本文提出的高度屬性判別算法的有效性和正確性。

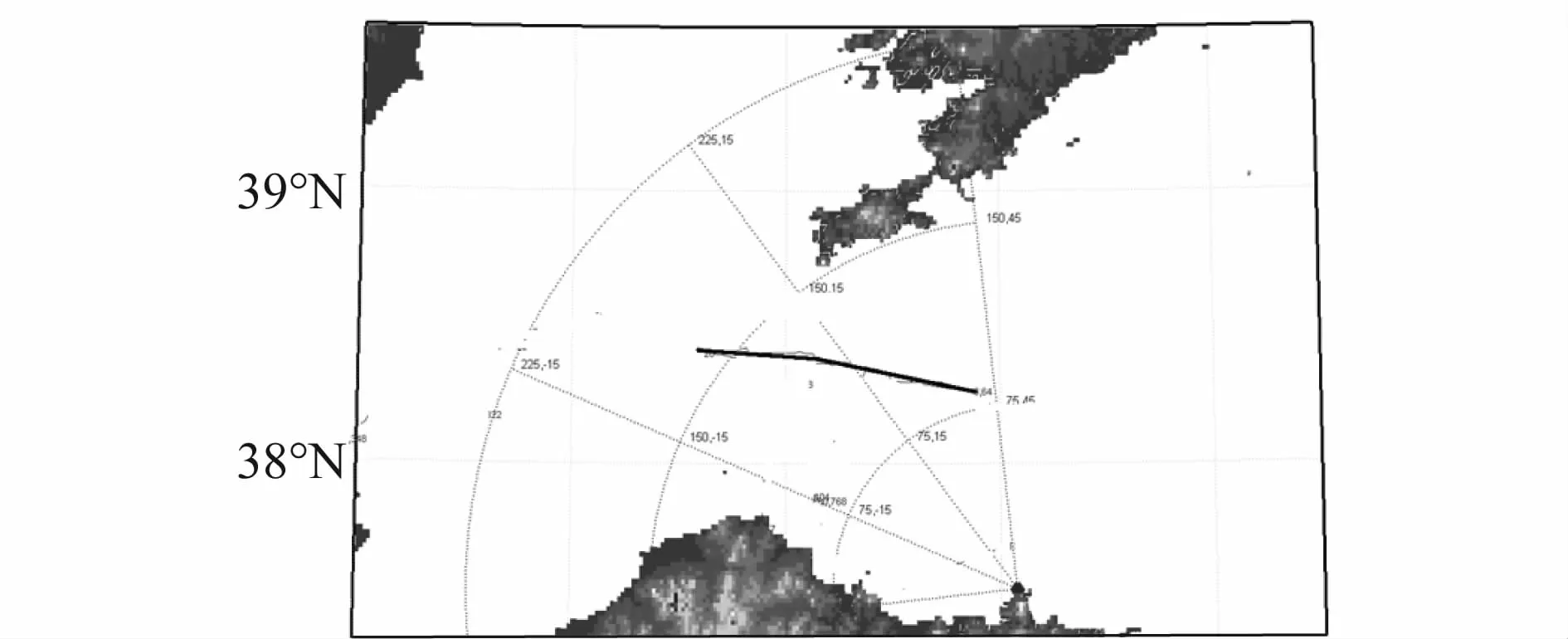
圖7 目標航跡

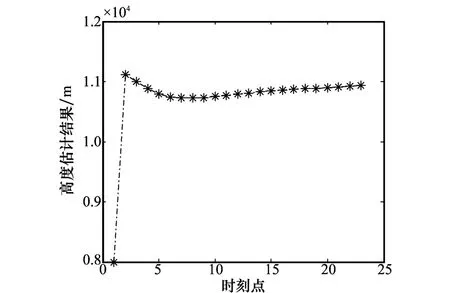
圖8 高度估計結果

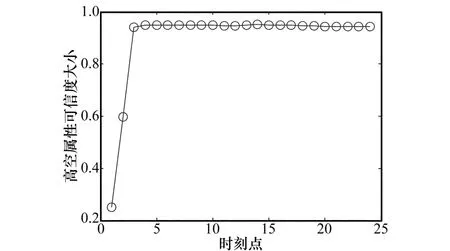
圖9 高空屬性判別可信度

第4批次目標飛行航跡如圖10所示，航跡圖中粗線為要處理的非合作民航目標。其高度估計結果和目標高度屬性判別結果如圖11和圖12所示。

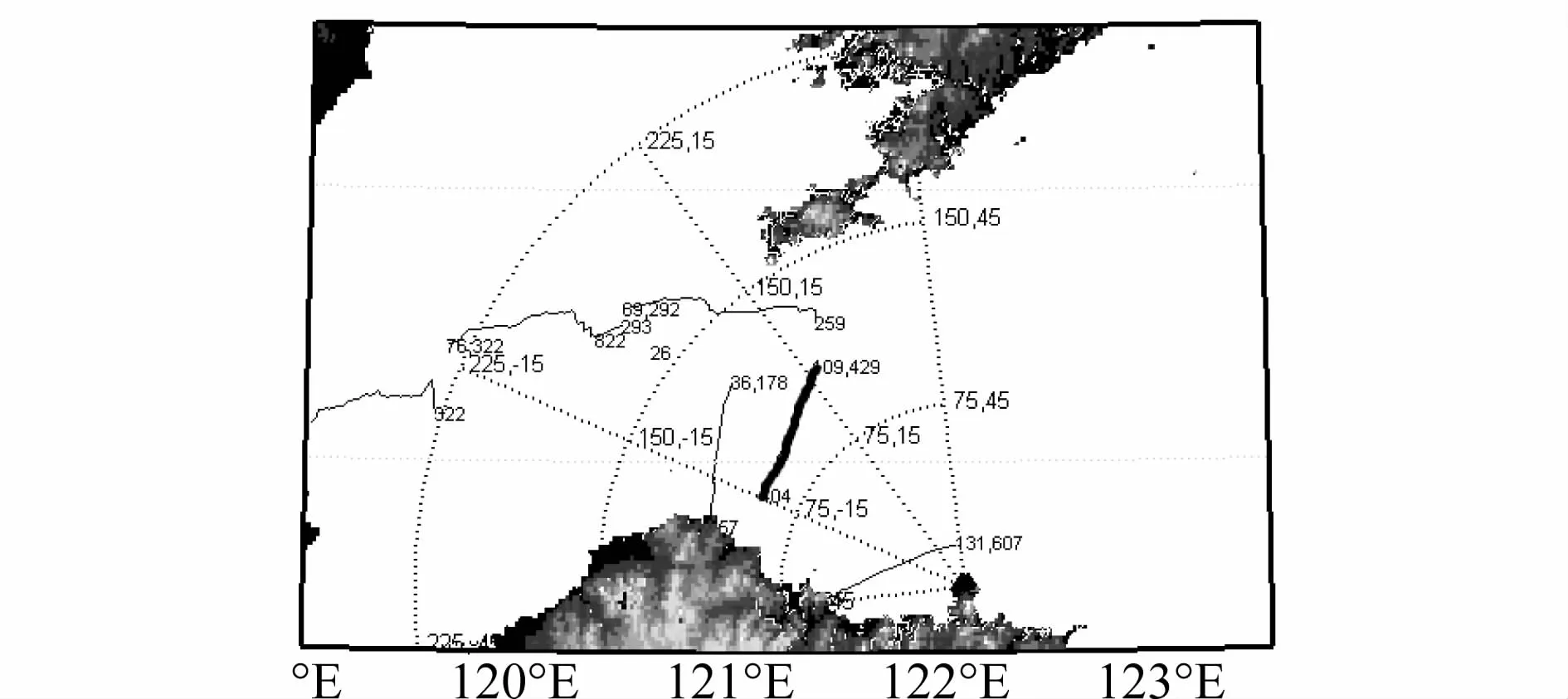
圖10 目標航跡

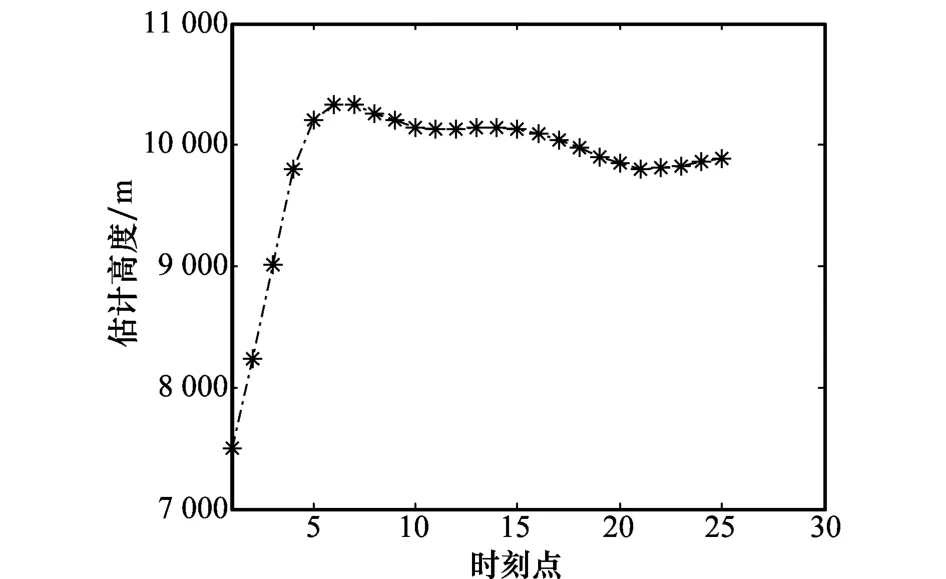
圖11 高度估計結果

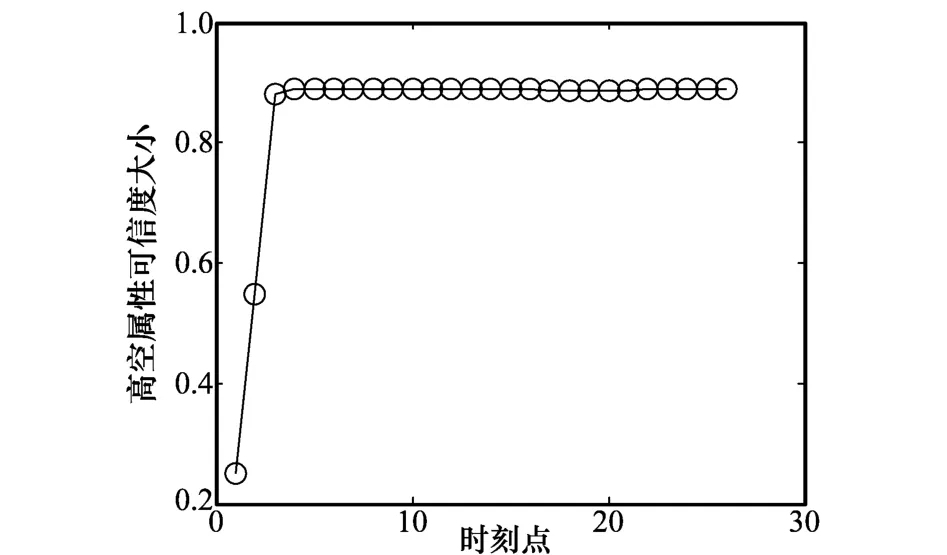
圖12 高空屬性判別可信度

由圖11可見，目標高度估計結果為9.7 km左右，圖12所示的高度屬性判別可信度顯示目標為高空屬性，屬性判別正確，高空屬性可信度為90%。從圖10所示的目標航跡可見，目標從山東飛往大連方向，航向速度為730 km／h。根據經驗可知，國內民航飛機一般為波音737類型中型飛機，飛行高度在9 km左右。因此，本試驗結果表明，高度估計誤差在10%左右，目標高度屬性判別正確。

4 結 論

本文利用垂直極化電波在高空和低空高度范圍內的傳播衰減的不同特性，提出一種基于信號回波強度信息的目標高度屬性判別算法，首次解決了HFSWR飛行目標高度屬性判別問題。這種屬性判別算法不僅判別目標高度屬性，而且給出了高度屬性判別可信度。實測數據處理表明，本算法能夠在5個觀測時間內判別出目標高度屬性，屬性判別可信度達到90%。

［1］Anderson S J.Optimizing HF radar siting for surveillance and remote sensing in the Strait of Malacca［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（3）：1805-1816.

［2］Xie J，Sun M，Ji Z.First-order ocean surface cross section for shipborne HFSWR［J］.Electronics Letters，2013，49（16）：1025 -1026.

［3］Zhou H，Wen B，Wu S.Ionospheric clutter suppression in HFSWR using multilayer crossed-loop antennas［J］.IEEE Geoscience and Remote Sensing Letters，2014，11（2），429-433.

［4］Grosdidier S，Forget P，Barbin Y，et al.HF bistatic ocean doppler spectra：simulation versus experimentation［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，52（4），2138-2148.

［5］Bruno L，Braca P，Horstmann J，et al.Experimental evaluation of the range doppler coupling on HF surface wave radars［J］.IEEE Geoscience and Remote Sensing Letters，2013，10（4）：850-854.

［6］Sathyan T，Chin T J，Arulampalam S，et al.A multiple hypothesis tracker for multitarget tracking with multiple simultaneous measurements［J］.IEEE Journal of Selected Topics in Signal Processing，2013，7（2）：448-460.

［7］Abramovich Y I，Frazer G J，Johnson B A.Principles of mode selective MIMO OTHR［J］.IEEE Trans.on Aerospace and Electronic Systems，2013，49（3）：1839-1868.

［8］Skolnik M I.Introduction to radar system［M］.3rd ed.Zhuo Q S trans.Beijing：Publishing House of Electronics Industry，2006：392-393.（Skolnik M I.雷達系統導論［M］.3版.左群聲，譯.北京：電子工業出版社，2006：392-393.）

［9］Howland P E，Clutterbuck C F.Estimation of target altitude in HF surface wave radar［C］∥Proc.of the 7th International Conference on HF Radio Systems and Techniques，1997：296-300.

［10］Zhang S，Jin Y G，Yu C J.HPEKF algorithm of target altitude estimation initializing in HF surface wave radar［J］.Journal of Harbin Institute of Technology，2007，39（5）：726-729.（張碩，金永鎬，于長軍.高頻地波雷達目標高度估計起始的HPEKF算法［J］.哈爾濱工業大學學報，2007，39（5）：725-729.）

［11］Gai M J，Yi X，He Y，et al.An approach to tracking a 3D-target with 2D-Radar［C］∥Proc.of IEEE International Radar Conference，2005：763-768.

［12］Guo R J，Yuan Y S，Quan T F.Study of anti-weak aerial target tracking for high Frequency surface wave radar［J］.Acta Electronica Sinica，2005，16（2）：1586-1589.（郭汝江，袁業術，權太范.高頻地波雷達飛行小目標跟蹤方法研究［J］.電子學報，2005，16（2）：1586-1589.）

［13］Rotheram S.Ground-wave propagation.Part 1：Theory for short distances［J］.IEE Communications Radar and Signal Processing，1981，128（5）：275-284.

［14］Rotheram S.Ground-wave propagation.Part 2：Theory for short distances［J］.IEE Communications Radar and Signal Processing，1981，128（5）：285-295.

Target flight mode identification with HFSWR

ZHAO Kong-rui1，YU Chang-jun2，LIU Ai-jun2，JIAN Wei-le2，QUAN Tai-fan2
（1.School of Electronics and Information Engineering，Harbin Institute of Technology，Harbin 150001，China；2.School of Information and Electrical Engineering，Harbin Institute of Technology（Weihai），Weihai 264209，China）

Fight altitude estimation of aircraft is a hotspot in high frequency surface wave radar（HFSWR）application which has not been resolved effectively.However，it is more meaningful and available to identify the flight mode of aircraft than cost too much time to estimate the target altitude in the engineering application.Based on the above viewpiont，an engineering method is proposed to solve the flight mode identification problem with the variation property of the propagation attenuation at different altitude intervals.This method can identify the target flight mode and evaluate the probability of the flight mode.Practical trials demonstrate that the proposed method can identifiy the target flight mode with a small quantity of measurement data，the aircraft flight mode can be identified correctly and the identification probability achieves more than 90%.

high frequency surface wave radar（HFSWR）；flight mode；propagation attenuation

TN 959.72 文獻標志碼：A DOI：10.3969／j.issn.1001-506X.2015.09.10

趙孔瑞（1984-），男，博士，主要研究方向為高頻地波雷達信號處理。

E-mail：zhaokongrui＠163.com

于長軍（1962-），男，教授，博士，主要研究方向為雷達系統及信號處理。

E-mail：yuchangjun＠hit.edu.cn

劉愛軍（1971-），男，副教授，博士，主要研究方向為雷達信號處理與通信系統。

E-mail：hitlaj＠163.com

菅維樂（1978-），男，講師，主要研究方向為雷達信號處理。

E-mail：jianweile＠sina.com

權太范（1949-），男，教授，主要研究方向為高頻地波雷達信號處理、數據處理及多源信息融合。

E-mail：quantaif＠hit.edu.cn

1001-506X（2015）09-2018-05

2014-04-30；

2015-01-04；網絡優先出版日期：2015-06-08。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150608.1031.001.html

國家自然科學基金（61171188）資助課題