基于模糊信息粒化SVM時序回歸CPI預測
路世昌,趙博琦,畢建武
0 引言
消費者物價指數(CPI),是以與居民生活有關的產品及勞務等價格統計出來的綜合指標,可用來衡量物價的變動情況[1]。CPI涉及經濟發展,關乎社會和諧,維系人民生計,是管理者制定宏觀經濟政策、分析貨幣市場和債券市場及央行公開市場業務的重要參考依據,歷來備受政府和民眾關注。因此對CPI的精確預測具有重要的現實意義[2]。然而CPI受到多種不確定因素影響,很難對其進行非常精確的預測,這時對CPI變化范圍及走勢進行預測顯得更為重要。模糊信息粒化能夠通過群體中個體之間的協作和信息共享來尋找最優解,降低維數,加快擬合收斂。支持向量機(SVM)有優良的泛化能力,并且在解決小樣本、非線性及高維空間表現出了很多的優勢,能夠避免災難維數,局部極值等問題。本文將模糊信息粒化方法與支持向量機相結合,提出了基于模糊信息粒化SVM時序回歸CPI預測模型,該模型能夠給出CPI較精確的變化范圍及走勢,為經濟政策以及宏觀經濟決策提供依據。
1 模糊信息粒化支持向量機模型
1.1 模糊信息粒化
信息粒化就是將一個整體分解為一個個的部分進行研究,每個部分為一個信息粒。信息粒就是一些由于難以區別、或相似接近或具備某種功能而結合在一起的元素的集合。L.A.Zadeh于1979年在模糊集合論的基礎上首次提出并討論了模糊信息粒化問題,并給出了一種數據里的命題刻畫[3~5]:
gΔ=(x is G)is λ
其中,x是論域U中取值的變量,G是U的模糊子集,由隸屬函數μG來刻畫。λ表示可能性概率。一般假設U為實數集合R,G是U的凸模糊子集,λ是單位區間的模糊子集。
模糊信息粒就是以模糊集形式表示信息粒。在對時間序列進行模糊粒化時主要包括劃分窗口和模糊化兩個步驟。其中模糊化是最為關鍵的部分,也就是在所給窗口上建立一個能取代原來窗口信息的模糊集。本文采用的是W.Pcdrycz粒化方法[6]。該方法基本思想:
⑴模糊粒子能夠合理代表原始數據;
⑵模糊粒子要有一定的特殊性。
為找到兩者最佳平衡,可建立如下函數:
QA=MA/NA
其中MA為滿足⑴,NA為滿足⑵。
本文采用三角形模糊粒子,其隸屬函數如下;
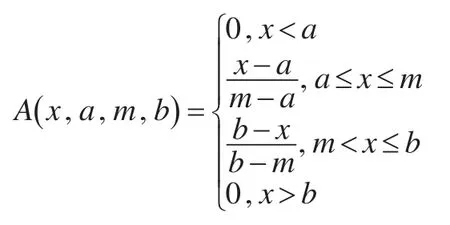
Low,R,Up為模糊粒子的三個參數,對于三角型模糊數而言,分別代表a,m,b三個參數。其中Low描述原始數據變化的最小值,R反映變化的平均水平,Up則表示原始數據變化的最大值。
1.2 支持向量機[7~10]
支持向量機是20世紀90年代由Vapnik等提出的一種研究小樣本、小概率事件的神經網絡模型,能夠根據有限的樣本信息在模型的復雜性和學習能力之間尋求最優解。與神經網絡相比,支持向量機是基于統計學習理論的小樣本學習方法,采用結構風險最小化原則,具有很好的泛化性能;而神經網絡是基于大樣本的學習方法,采用經驗風險最小化原則。基本思想:通過非線性映射將原空間映射至高維特征空間,將搜索到的最優線性回歸超平面問題轉化為求解凸約束下的凸規劃問題。
支持向量機的基本想是通過事先確定的非線性映射將輸入向量映射的一個高維特征空間(Hilbert空間),然后在此高維空間中再進行回歸。
首先將輸入量x通過映射Φ:Rn→H映射到高維特征空間H中用函數
f(x)=ω·Φ(x)+b
擬合數據(xi,yi)目標函數式為:
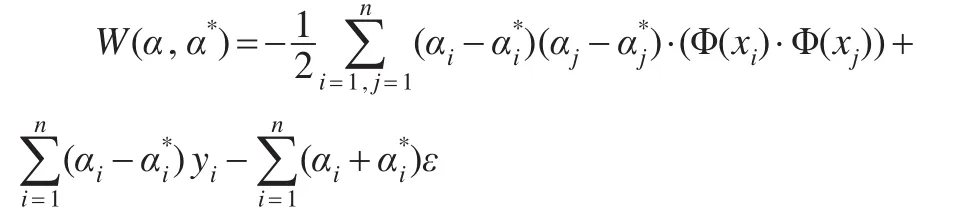
式中涉及到高維特征空間點積運算Φ(xi)·Φ(yi),而且函數Φ是未知的,高維的。支持向量機理論只考慮高維特征空間的點積運算K(xi,yi)=Φ(xi)·Φ(yi),而不直接使用函數Φ。稱K(xi,yi)為核函數,核函數的選取應使其為高維特征空間的一個點積,核函數的類型有多種,本文選取徑向基核函數:
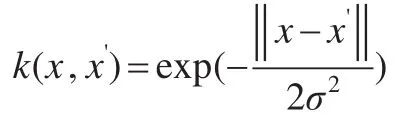
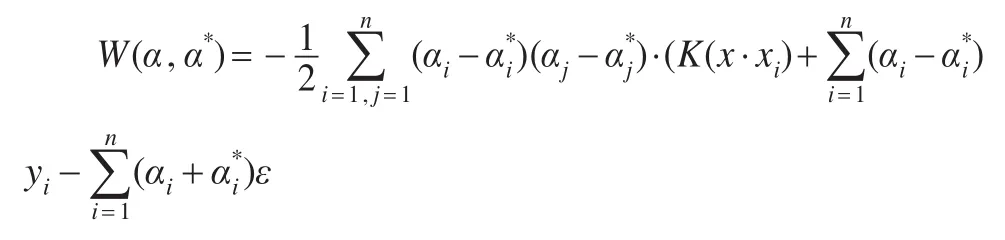
得可求得合函數的表示式為:

1.3 模糊信息粒化支持向量機CPI預測模型
模糊信息粒化支持向量機CPI預測流程如下:
(1)獲取歷年CPI數據,并進行輸入;
(2)對CPI數據進行模糊信息粒化處理;
(3)采用交叉驗證的方法,利用模糊粒化處理后的數據對SVM進行訓練確定最優參數c和g;
(4)利用最優c和g建立模糊信息粒化SVM模型對CPI進行預測;
(5)輸出CPI變化趨勢及變化空間。
模型流程圖如下:

圖1 模型流程圖
2 實證分析
本文以2000年1月份到2014年1月份月度CPI為研究對象,其中2013年11月之前的數據用于建立模型,之后的數據用于模型檢驗。數據來源于國家統計局官方網站。序列時序圖見圖2。
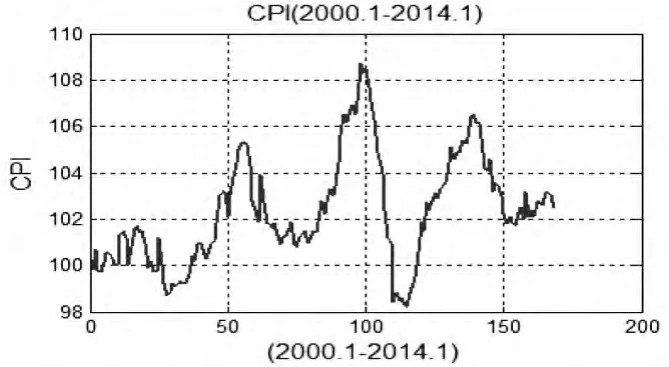
圖2 CPI序列時序
2.1 模糊信息粒化處理
本文將3個月的CPI作為一個窗口大小,得窗口數目為原始數據長度除以3后取整。在Matlab 2012a環境下進行模糊粒化處理結果見圖3。
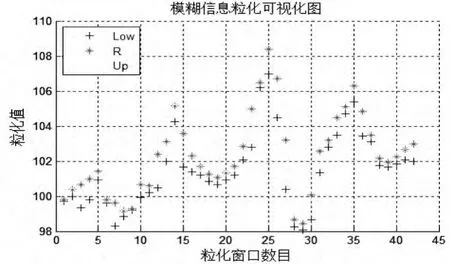
圖3 模糊粒化效果
2.2 利用SVM對模糊粒化數據進行預測
在Matlab 2012a環境下利用SVM對三個模糊粒子Low,R,Up進行回歸預測,將原始數據歸一化到[0,1],采用交叉驗證對SVM進行參數尋優,結果如下:
Low:交叉驗證 MSE=0.0116525,Best c=2,Best g=0.125;
R:交叉驗證MSE=0.0670537,Best c=4,Best g=0.125;
Up:交叉驗證 MSE=0.0683058,Best c=5.65685,Best g=0.125
利用最優參數進行擬合及預測,三個模糊粒子Low,R,Up擬合結果見圖4,預測結果見表1。
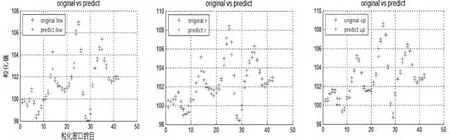
圖4 信息粒化擬合結果

表1 預測結果及比較
由表1可知本文預測的CPI變化范圍是準確的,精確度較高,而且可以看出這三個月CPI數值整體呈略微下降趨勢。表明該模型預測結果可靠,能夠為相關決策提供依據,具有一定的實用性。
3 結論
⑴將模糊信息粒化模型與SVM相結合,提出了提出了基于模糊信息粒化SVM回歸CPI預測模型,該模型能夠綜合利用模糊信息粒化及SVM的優點。利用該模型進行實際預測,預測結果變化范圍及變化趨勢與實際相符,證明了該模型的有效性和實用性。
⑵該模型是基于歷史CPI數據建立的,沒有考慮經濟變化,物價水平等各種不確定性因素,模型還有待于進一步完善。
[1] 郭曉峰.基于ARIMA模型的中國CPI走勢預測分析[J].統計與決策,2012,(11).
[2] 韓春蕾,高婉君.我國月度CPI的組合預測及分析[J].統計與決策,2014,(1).
[3] 張鈴,張鈸.模糊商空間理論(模糊粒度計算方法)[J].軟件學報,2003,14(4).
[4] 張蕾,周洲.基于小波和信息粒化的BP神經網絡的軸承故障診斷[J].機械科學與技術,2012,31(1).
[5] Bargiela A,Pedrycz W.Granular Computing:An Introduction[M].Dodrecht:Kluwer Academic Publishers,2003.
[6] MATLAB中文論壇.MTALAB神經網絡30個案例分析[M].北京:北京航空航天大學出版社,2010.
[7] Nello Cristianini John Shawe-Talor.支持向量機導論[M].(李國正,王猛,曾華軍譯).北京:電子工業出版社,2004.
[8] Cao L J.Support Vector Machines Experts for Forecasting[J].Neuro?computing,2003,(51).
[9] Chen L.Hourly Water Demand Forecast Model Based on Support Vec?tor Machine[J].Journal of Basic Science and Engineering,2009,17(4).
[10] 劉希亮,趙學勝,陸鋒.基于GA-SVM的露天礦拋擲爆破拋擲率預測[J].煤炭學報,2012,37(12).

