基于輸入限制的I-ELM機車熱軸等級判別模型

宋平崗，林家通，康水華，楊云

(華東交通大學 電氣與電子工程學院，南昌 330013)

滾動軸承是機車走行部的關鍵零件，其狀況直接影響機車的性能與安全[1]。高速運行中，如果軸承發生故障甚至卡死，會產生熱軸現象，不能及時處理將造成切軸甚至顛覆事故[2]。據統計，80%以上的火車翻車事故由熱軸造成。

目前，廣泛采用紅外線軸溫探測系統(Trace Hotbox Detection System, THDS)監控熱軸現象，但其實際應用中預報兌現率普遍較低，誤報率較高[3-5]。由于熱軸判別的復雜性，目前THDS設備根據歷史經驗設定熱軸判別閾值，無法直接滿足實際應用要求。為提高溫度判別準確率，文獻[6]提出使用模型算法對軸溫建立識別模型，實現對軸承溫度的模糊判別，但其存在隸屬度函數設計困難，參數設計主觀性強等不足。文獻[7]提出了基于模糊神經網絡的熱軸判別模型，準確率較高,但存在神經訓練層及隱含神經元多，計算速度慢等缺陷。

針對上述問題，引入增量型極限學習機(Incremental Extreme Learning Machine, I-ELM)算法，該算法具有學習速度快、參數少、精度高等優勢[8-10]。I-ELM算法隨機產生輸入層與隱含層間的連接權值及隱含層神經元的閾值，且在訓練過程中無需調整，只需設置隱含層神經元的個數便可獲得唯一的最優解，通過不斷增加隱含層神經元個數減小訓練誤差，提高網絡精度。針對機車軸溫的非線性復雜多變特性，提出帶輸入限制的極限學習機，對熱軸級別進行判別，并將其應用于和諧型機車軸承溫度監測報警裝置中。

1 機車熱軸判別模型

1.1 背景分析

軸承內部的摩擦是其主要熱源。從生熱的角度考慮，整體生熱法和局部生熱法以實驗室測量結果為基礎，總結出的經驗公式并不能完全適用于機車軸承復雜溫度場情況。熱網絡法和有限元法采用理論分析，事先假設了某些特定條件，結論形式復雜且計算量大，無法滿足機車軸溫故障快速報警的要求[11]。

機車軸承運行溫度的影響因素多而復雜，且相互交叉關聯。THDS設備在實際中判別效果并不理想，主要因為機車運行在不同區間時，溫度、氣候等環境因素存在較大變化，且車型、車種，軸承結構、運行速度、負載情況等內在因素差異都直接影響機車軸承的運行溫度。這些復雜且密切關聯的因素決定了機車軸承溫度模型的復雜性。

目前，THDS設備生產廠家常根據歷史經驗設定熱軸判別的閾值。由于機車的運行環境及自身運行情況存在變化，固定的閾值無法適應實際應用需求。因此，熱軸級別判斷沒有固定的公式與模型，可以視作其中內在關聯因素發生作用，直接體現在軸承溫度上。在此，分析軸承溫度與其熱軸級別，并采用神經網絡訓練的中間隱含層表述其內在關系。

1.2 機車熱軸判別模型

極限學習機(Extreme Learning Machine，ELM)是典型的單隱含層前饋神經網絡結構，由輸入層、隱含層和輸出層組成，輸入層與隱含層、隱含層與輸出層神經元之間全連接。

熱軸判別受諸多因素影響，一般不直接使用軸溫作為熱軸判別指標，而是使用軸溫溫升[5-7]。軸溫溫升是指軸溫與環境溫度之差，選取溫升T1、列溫升T2、輛溫升T3作為模型的輸入，其具體含義見表1。

表1 模型輸入含義

模型的輸出為熱軸等級G，沿用鐵路系統做法將熱軸等級分為正常、微熱、強熱、激熱共4級，分別用1，2，3，4表示輸出。則ELM神經網絡結構如圖1所示。

圖1 ELM神經網絡結構

設隱含層神經元為n，則輸入層與隱含層之間的連接權值w為

(1)

式中：wji為輸出第i個神經元與隱含層第j個神經元間的連接權值,j=1,2,…,n;i=1,2,3。

隱含層與輸出層間的連接權值β為

β=[β1,β2,…,βn]T，

(2)

式中：βj為第j個神經元與輸出神經元的連接權值。

隱含層神經元的閾值b為

b=[b1,b2,…,bn]T。

(3)

設隱含層激活函數為g(x)，則具有Q個訓練樣本的神經網絡輸出G可以表示為

(4)

其中wi=[w11,w12,w13]，(4)式可以進一步表示為

Hβ=GT，

(5)

H(w1,w2,…,wn,b1,b2,…,bn,T1,T2,…,TQ)=

(6)

若給定滿足某些條件的激活函數，如sigmoid，sine，hardlim和RBF函數，則神經網絡的輸出可以任意精度逼近目標函數[12-13]。因此,在極限學習機算法中，連接權值w和閾值b在訓練中隨機選擇且在訓練中保持不變。而隱含層與輸出層間的連接權值β可以通過求解以下方程組的最小二乘解獲得

(7)

其解為

(8)

式中：H+為隱含層輸出矩陣H的Moore-penrose廣義逆矩陣。

1.3 隱含層神經元數目確定

隱含層神經元數目太少或太多對神經網絡的性能都有影響，而隨著隱含層神經元數目的增加，增量型極限學習機的輸出誤差趨勢逐漸減小并趨近零[14]，即第k+1次迭代所獲取的網絡輸出誤差小于第k次迭代，不會出現過擬合問題。

因此，選取隱含層神經網絡具體做法是：首先給定隱含層神經元初值n，訓練誤差η，如果網絡輸出誤差E大于訓練誤差η，則增加隱含層神經元數目，重新訓練網絡，直至E<η。

1.4 基于輸入限制的I-ELM熱軸等級判別模型

根據電力機車軸溫的特性，通常THDS設備在軸承溫升達到40 ℃時預報微熱，溫升超過70 ℃時預報激熱[6]。但是簡單的“一刀切”往往會造成判斷錯誤，故采用I-ELM熱軸等級判別模型。在軸承溫升低于30 ℃時，可以不通過ELM算法即可明確判定為正常運轉溫度；同樣，溫度超過100 ℃的強烈發熱的情況下，可以直接判定為激熱。判別表達式為

(9)

通過溫升能夠直接判斷熱軸等級的數據，減小ELM的計算量，從而提高算法的效率。因此，基于輸入限制的I-ELM熱軸等級判別模型實現步驟為：

1)處理數據并獲取Q個訓練樣本，給定訓練誤差η；

2)設隱含層神經元數目初值n=0, 樣本訓練誤差E；

3)設隱含層節點n=n+1；

4)隨機產生輸入層與隱含層之間的連接權值w及隱含層神經元的閾值b；

5)選擇sigmoid函數為激發函數，并根據(6)式計算隱含層輸出矩陣H；

6)根據(8)式計算隱含層與輸出層間的連接權值β；

7)根據(4)式計算神經網絡的輸出G；

8)計算訓練樣本誤差E

(10)

若E<η，則終止訓練，否則跳至第3)步；

9)限制輸入，篩選測試樣本。溫升低于30 ℃時熱軸等級為1，溫升大于100 ℃時熱軸等級為4。篩選后組成新的測試樣本；

10)測試訓練網絡。將新的測試樣本輸入訓練好的網絡，將預測值與測試樣本實際輸出值進行對比，檢驗模型判別能力。

2 仿真分析

仿真試驗基于MATLAB7.8平臺，共選取60個樣本，其中正常、激熱、強熱樣本各10個，微熱樣本30個。為達到較好的訓練網絡，每個熱軸等級的樣本數據按照訓練樣本與測試樣本4∶1的比例選取，即訓練樣本48個，測試樣本12個。首先設定隱含層神經元初值L為30，訓練允許誤差E為4%，進行隱含層神經元個數選取，結果見表2。

表2 不同隱含層神經元個數的誤差

由表2可知，隨著隱含層數目的增加，誤差E有波動，但總體趨勢是誤差越來越小。當L=44時，誤差E=2.08%，符合要求，因此將隱含層神經元數目固定為44。將訓練好的網絡用于測試樣本,預測結果與真實值的對比如圖2所示，分類正確率達91.667%，其中熱軸等級為正常運轉、微熱和激熱分類正確率為100%。由于樣本數較小，神經網絡的訓練精度較差。如果強熱樣本數再多一些，分類正確率還會有所提高。

圖2 ELM模型熱軸等級判別結果

為進一步驗證模型的有效性，采用傳統的BP神經網絡和RBF神經網絡進行分析，結果如圖3和圖4所示。3種模型運行時間和判別準確率的對比結果見表3，ELM的效率及準確率均高于其他2種模型。

圖3 BP模型熱軸等級判別結果

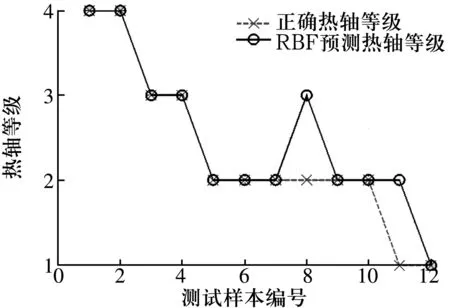
圖4 RBF模型熱軸等級判別結果

表3 算法運行時間

3 算法應用

根據上述模型，設計了和諧型機車軸承溫度監測報警裝置，其系統結構如圖5所示，由傳感器、接線盒、通信總線、主機和顯示器等組成。系統采用1-wire總線數字溫度傳感器，每個傳感器采用吸附式安裝方式固定到每個溫度測量點[15]。傳感器安裝部位如圖6所示，每個軸位測量電動機大、小端，車軸左、右端，抱軸左、右端等6個軸溫測量點，每個軸位還可接1個環境溫度探頭，即每個主機上布置28個溫度探頭。

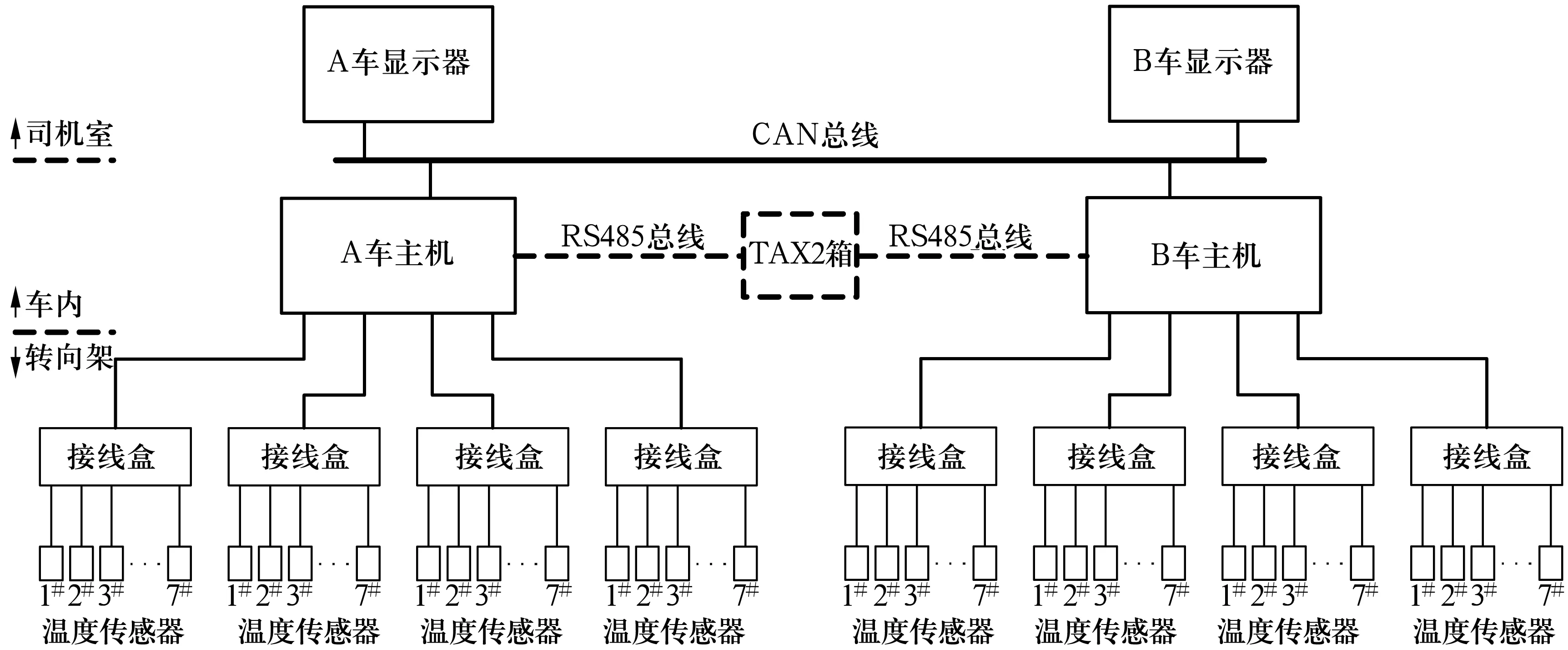
圖5 系統整體結構框圖

圖6 系統溫度傳感器安裝實物圖

采用Contex-M3處理芯片ARM5749作為主控處理器。主機測量的溫度數據經ARM5749計算處理后在顯示器上顯示，同時通過色塊警示及蜂鳴器報警，溫度顯示與報警效果如圖7所示。

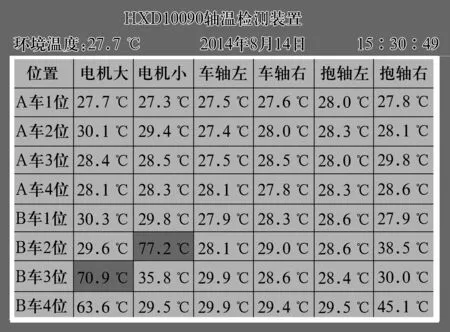
圖7 系統溫度顯示及報警界面

在系統設計中，系統需要完成傳感器溫度值的采集、計算、分析、數據處理、報警等級識別及液晶顯示驅動等。在程序設計中根據經驗選取40個輸入、輸出樣本作為固定的訓練參數，并根據測量診斷結果自動增加或更新20個輸入、輸出結果作為實時變化的訓練參數。具體ELM算法流程如圖8所示。

圖8 系統整體結構框圖

4 結束語

將ELM模型應用于機車熱軸級別判別，并結合熱軸自身特性提出了基于輸入限制I-ELM判別方法。根據設計精度要求選定隱含層神經元數目，針對多數的常規低溫升情況與少量特高溫升故障情況，不輸入ELM網絡而直接判別，極大提高了模型的判別效率。

仿真結果表明，ELM熱軸等級判別模型不僅判別準確性有所提高，而且大大縮短了運行時間。多年實際應用表明，熱軸等級模型判別準確，運行效果良好。