如何用頻率來估計(jì)概率
顧長亮
在蘇科版初中數(shù)學(xué)課本里所學(xué)習(xí)的概率計(jì)算問題有以下類型:第一類是可以列舉有限個(gè)等可能發(fā)生的結(jié)果的概率計(jì)算問題(一步試驗(yàn)直接列舉,兩步以上的試驗(yàn)可以借助樹狀圖或表格列舉),比如擲一枚均勻硬幣的試驗(yàn);第二類是用試驗(yàn)或者模擬試驗(yàn)的數(shù)據(jù)計(jì)算頻率,并用頻率估計(jì)概率的概率計(jì)算問題,比如擲圖釘?shù)脑囼?yàn)。在八年級(jí)的數(shù)學(xué)學(xué)習(xí)中概率的計(jì)算,主要是第二類題型,我們知道頻率是研究概率的基礎(chǔ),所以利用頻率估計(jì)概率的試題頻頻出現(xiàn)在各地的中考試卷中,下面以中考題為例,來剖析這一類題型的解法。
一、填空題中的用頻率估計(jì)概率
例1.在課外活動(dòng)中,小明同學(xué)在相同的條件下做了某種作物種子發(fā)芽的實(shí)驗(yàn),結(jié)果如下表所示:

由此估計(jì)這種作物種子發(fā)芽率約為 (精確到0.01).
解:由公式種子的發(fā)芽率= 可求出種子的發(fā)芽率為0.939,因?yàn)榫_到0.001故答案為0.94.
點(diǎn)評(píng):本題考察了百分率問題(1)種子的發(fā)芽率= ;(2)注意括號(hào)的中的要求為精確到0.01
例2.有一箱規(guī)格相同的紅、黃兩種顏色的小塑料球共1000個(gè).為了估計(jì)這兩種顏色的球各有多少個(gè),小明將箱子里面的球攪勻后從中隨機(jī)摸出一個(gè)球記下顏色,再把它放回箱子中,多次重復(fù)上述過程后,發(fā)現(xiàn)摸到紅球的頻率約為0.6,據(jù)此可以估計(jì)紅球的個(gè)數(shù)約為 .
解:解:∵摸到紅球的頻率約為0.6,∴紅球所占的百分比是60%.∴1000×60%=600.
故答案為:600.
點(diǎn)評(píng):本題考查用頻率估計(jì)概率,因?yàn)槎啻沃貜?fù)上述過程后,發(fā)現(xiàn)摸到紅球的頻率約為0.6,所以紅球所占的百分比也就是60%,根據(jù)總數(shù)可求出紅球個(gè)數(shù).
二、選擇題中的用頻率估計(jì)概率
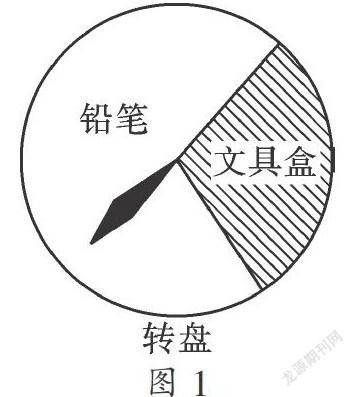
例3.“六·一”兒童節(jié),某玩具超市設(shè)立了一個(gè)如圖所示的可以自由轉(zhuǎn)動(dòng)的轉(zhuǎn)盤,開展有獎(jiǎng)購買活動(dòng).顧客購買玩具就能獲得一次轉(zhuǎn)動(dòng)轉(zhuǎn)盤的機(jī)會(huì),當(dāng)轉(zhuǎn)盤停止時(shí),指針落在哪一區(qū)域就可以獲得相應(yīng)獎(jiǎng)品.下表是該活動(dòng)的一組統(tǒng)計(jì)數(shù)據(jù):
下列說法不正確的是( )
A.當(dāng)n很大時(shí),估計(jì)指針落在“鉛筆”區(qū)域的頻率大約是0.70
B.假如你去轉(zhuǎn)動(dòng)轉(zhuǎn)盤一次,獲得鉛筆的概率大約是0.70
C.如果轉(zhuǎn)動(dòng)轉(zhuǎn)盤2000次,指針落在“文具盒”區(qū)域的次數(shù)大約有600次
D.轉(zhuǎn)動(dòng)轉(zhuǎn)盤10次,一定有3次獲得文具盒

解:由表中提供的信息可知,只有“轉(zhuǎn)動(dòng)轉(zhuǎn)盤10次,一定有3次獲得文具盒”的判斷不一定正確,故應(yīng)選D.
點(diǎn)評(píng):正確正解頻率與概率之間的關(guān)系是求解此類問題的關(guān)鍵. 由表中提供的信息,我們可以知道,當(dāng)n很大時(shí),指針落在“鉛筆”區(qū)域的頻率趨于0.70,由此,由頻率與概率之間的關(guān)系可知,假如你去轉(zhuǎn)動(dòng)轉(zhuǎn)盤一次,獲得鉛筆的概率大約是0.70,如果轉(zhuǎn)動(dòng)轉(zhuǎn)盤2000次,指針落在“文具盒”區(qū)域的次數(shù)大約有2000次×(1-0.7)=600次,而將轉(zhuǎn)盤轉(zhuǎn)動(dòng)轉(zhuǎn)盤10次,卻不一定有3次獲得文具盒.
三、解答題中的用頻率估計(jì)概率
例4.六一期間,某公園游戲場(chǎng)舉行“迎奧運(yùn)”活動(dòng).有一種游戲的規(guī)則是:在一個(gè)裝有6個(gè)紅球和若干個(gè)白球(每個(gè)球除顏色外其他都相同)的袋中,隨機(jī)摸一個(gè)球,摸到一個(gè)紅球就得到一個(gè)奧運(yùn)福娃玩具.已知參加這種游戲活動(dòng)為40 000人次,公園游戲場(chǎng)發(fā)放的福娃玩具為10 000個(gè).
(1)求參加一次這種游戲活動(dòng)得到福娃玩具的頻率;
(2)請(qǐng)你估計(jì)袋中白球接近多少個(gè)?
分析(1)由40 000人次中公園游戲場(chǎng)發(fā)放的福娃玩具為10 000個(gè),結(jié)合頻率的意義可直接求得.(2)由概率與頻率的關(guān)系可估計(jì)從袋中任意摸出一個(gè)球,恰好是紅球的概率,從而引進(jìn)未知數(shù),構(gòu)造方程求解.
解(1)因?yàn)?= ,所以參加一次這種游戲活動(dòng)得到福娃玩具的頻率為 .
(2)因?yàn)樵囼?yàn)次數(shù)很大,大數(shù)次試驗(yàn)時(shí),頻率接近于理論頻率,
所以估計(jì)從袋中任意摸出一個(gè)球,恰好是紅球的概率是 .
設(shè)袋中白球有x個(gè),則根據(jù)題意,得 = ,解得x=18.經(jīng)檢驗(yàn)x=18是方程的解.
所以估計(jì)袋中白球接近18個(gè).
點(diǎn)評(píng):利用頻率估計(jì)概率,并以此引進(jìn)未知數(shù)構(gòu)造方程是求解此類問題的常用方法,同學(xué)們?cè)趯W(xué)習(xí)時(shí)應(yīng)注意體會(huì)和運(yùn)用.
例5.研究問題:一個(gè)不透明的盒中裝有若干個(gè)只有顏色不一樣的紅球與黃球,怎樣估算不同顏色球的數(shù)量?
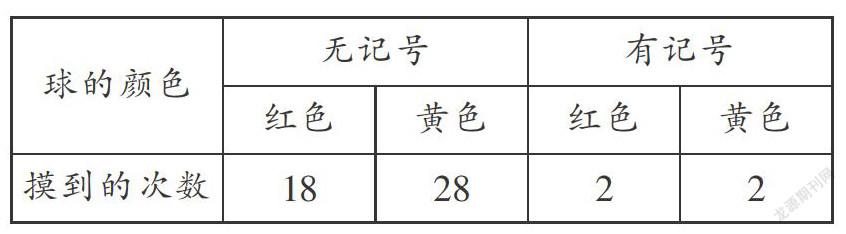
操作方法:先從盒中摸出8個(gè)球,畫上記號(hào)放回盒中,再進(jìn)行摸球?qū)嶒?yàn),摸球?qū)嶒?yàn)的要求:先攪拌均勻,每次摸出一個(gè)球,放回盒中,再繼續(xù).
點(diǎn)評(píng):(1)根據(jù)表格數(shù)據(jù)可以得到50次摸球?qū)嶒?yàn)活動(dòng)中,出現(xiàn)紅球20次,黃球30次,由此即可求出盒中紅球、黃球各占總球數(shù)的百分比;
(2)由題意可知50次摸球?qū)嶒?yàn)活動(dòng)中,出現(xiàn)有記號(hào)的球4次,由此可以求出總球數(shù),然后利用(1)的結(jié)論即可求出盒中紅球.
此題主要考查了利用頻率估計(jì)概率的問題,首先利用模擬實(shí)驗(yàn)得到盒中紅球、黃球各占總球數(shù)的百分比,然后利用百分比即可求出盒中紅球個(gè)數(shù).

