生活中的“概率”
陳國(guó)寶
生活中數(shù)學(xué)無(wú)處不在,隨著科學(xué)的發(fā)展,數(shù)學(xué)在生活中的應(yīng)用越來(lái)越廣;概率與我們的生活是息息相關(guān)的,學(xué)好概率可以讓我們能更理智的更聰明的處理好我們生活中遇到的種種問(wèn)題。
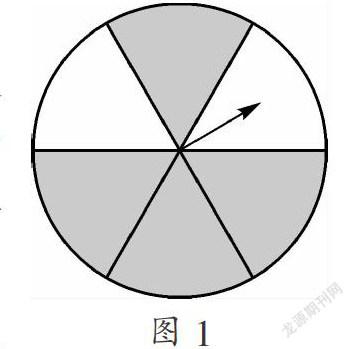
例1.(2014·蘇州)如圖,一個(gè)圓形轉(zhuǎn)盤(pán)被分成6個(gè)圓心角都為60°的扇形,任意轉(zhuǎn)動(dòng)這個(gè)轉(zhuǎn)盤(pán)1次,當(dāng)轉(zhuǎn)盤(pán)停止轉(zhuǎn)動(dòng)時(shí),指針指向陰影區(qū)域的概率是( )
考點(diǎn): 幾何概率.
分析: 設(shè)圓的面積為6,易得到陰影區(qū)域的面積為4,然后根據(jù)概率的概念計(jì)算即可.
解答: 解:設(shè)圓的面積為6,
∵圓被分成6個(gè)相同扇形,
∴每個(gè)扇形的面積為1,
∴陰影區(qū)域的面積為4,
例2.(2013·蘇州)任意拋擲一枚質(zhì)地均勻的正方體骰子1次,骰子的六個(gè)面上分別刻有1到6的點(diǎn)數(shù),擲得面朝上的點(diǎn)數(shù)大于4的概率為_(kāi)____.
考點(diǎn): 概率公式.3718684
分析: 根據(jù)擲得面朝上的點(diǎn)數(shù)大于4情況有2種,進(jìn)而求出概率即可.
解答: 解:擲一枚均勻的骰子時(shí),有6種情況,出現(xiàn)點(diǎn)數(shù)大于4的情況有2種,
例3.(2014·泰州)某籃球運(yùn)動(dòng)員去年共參加40場(chǎng)比賽,其中3分球的命中率為0.25,平均每場(chǎng)有12次3分球未投中.
(1)該運(yùn)動(dòng)員去年的比賽中共投中多少個(gè)3分球?
(2)在其中的一場(chǎng)比賽中,該運(yùn)動(dòng)員3分球共出手20次,小亮說(shuō),該運(yùn)動(dòng)員這場(chǎng)比賽中 一定投中了5個(gè)3分球,你認(rèn)為小亮的說(shuō)法正確嗎?請(qǐng)說(shuō)明理由.
考點(diǎn): 一元一次方程的應(yīng)用;概率的意義
分析: (1)設(shè)該運(yùn)動(dòng)員共出手x個(gè)3分球,則3分球命中0.25x個(gè),未投中0.75x個(gè),根據(jù)“某籃球運(yùn)動(dòng)員去年共參加40場(chǎng)比賽,平均每場(chǎng)有12次3分球未投中”列出方程,解方程即可;
(2)根據(jù)概率的意義知某事件發(fā)生的概率,就是在大量重復(fù)試驗(yàn)的基礎(chǔ)上事件發(fā)生的頻率穩(wěn)定到的某個(gè)值;由此加以理解即可.
3分球的命中率為0.25,是相對(duì)于40場(chǎng)比賽來(lái)說(shuō)的,而在其中的一場(chǎng)比賽中,雖然該運(yùn)動(dòng)員3分球共出手20次,但是該運(yùn)動(dòng)員這場(chǎng)比賽中不一定投中了5個(gè)3分球.
點(diǎn)評(píng): 此題考查了一元一次方程的應(yīng)用及概率的意義.解題關(guān)鍵是要讀懂題目的意思,根據(jù)題目給出的條件,找出合適的等量關(guān)系列出方程及正確理解概率的含義.