樹狀圖為概率題做導(dǎo)航
顧燕飛
在我們學(xué)習(xí)用列表法或畫樹狀圖法求概率時發(fā)現(xiàn),這兩個方法都可以列出所有可能的結(jié)果,而樹狀圖對于選取不重復(fù)、不放回的概率題能不重不漏、更加簡潔方便的表示;并且列表法只能適合于兩步完成的事件,而樹狀圖法卻適合兩步或兩步以上完成的事件,所以用好樹狀圖可以為我們解決概率題做好導(dǎo)航,達(dá)到一通百通的目的.
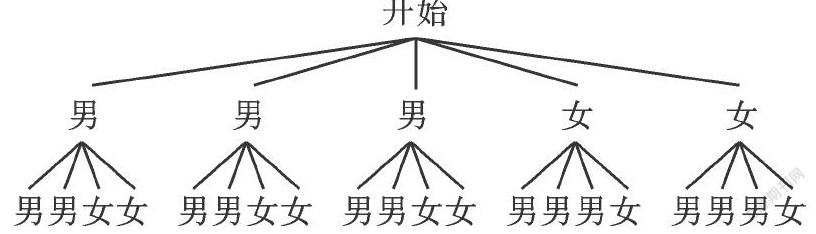
例1. (2014·淮安)班級準(zhǔn)備召開主題班會,現(xiàn)從由3名男生和2名女生所組成的班委中,隨機(jī)選取兩人擔(dān)任主持人,求兩名主持人恰為一男一女的概率.(請用“畫樹狀圖”或“列表”等方法寫出過程)
分析: 分析:本題根據(jù)題意在選擇畫出樹狀圖還是列表時,發(fā)現(xiàn)列表存在有部分重復(fù),要進(jìn)行刪除,所以不如選擇畫樹狀圖更為直接,然后由樹狀圖求得所有等可能的結(jié)果與兩名主持人恰為一男一女的情況,再利用概率公式即可求得答案.
例2.(2014·揚(yáng)州)商店只有雪碧、可樂、果汁、奶汁四種飲料,每種飲料數(shù)量充足,某同學(xué)去該店購買飲料,每種飲料被選中的可能性相同.
(1)若他去買一瓶飲料,則他買到奶汁的概率是 ;
(2)若他兩次去買飲料,每次買一瓶,且兩次所買飲料品種不同,請用樹狀圖或列表法求出他恰好買到雪碧和奶汁的概率.

分析: (1)由商店只有雪碧、可樂、果汁、奶汁四種飲料,每種飲料數(shù)量充足,某同學(xué)去該店購買飲料,每種飲料被選中的可能性相同,直接利用概率公式求解即可求得答案;
(2)首先根據(jù)題意可知,兩次所買飲料品種不同,如果選擇列表,必須刪除重復(fù)品種,所以選擇畫樹狀圖反而簡潔,然后由樹狀圖求得所有等可能的結(jié)果與他恰好買到雪碧和奶汁的情況,再利用概率公式即可求得答案.
解: (1)∵商店只有雪碧、可樂、果汁、奶汁四種飲料,每種飲料數(shù)量充足,某同學(xué)去該店購買飲料,每種飲料被選中的可能性相同,
例3(2011·蘇州)如圖所示的方格地面上,標(biāo)有編號1、2、3的3個小方格地面是空地,另外6個方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飛行的小鳥,將隨意落在圖中所示的方格地面上,求小鳥落在草坪上的概率;
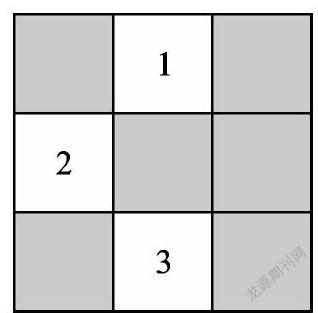
(2)現(xiàn)準(zhǔn)備從圖中所示的3個小方格空地中任選2個種植草坪,則編號為1、2的2個小方格空地種植草坪的概率是多少(用樹狀圖或列表法求解)?
分析:根據(jù)概率的求法,找準(zhǔn)兩點(diǎn):①全部情況的總數(shù);②符合條件的情況數(shù)目;二者的比值就是其發(fā)生的概率.使用樹狀圖分析時,可以不重不漏.
例4.(2011·鎮(zhèn)江)甲、乙、兩三個布袋都不透明,甲袋中裝有1個紅球和1個白球;乙袋中裝有一個紅球和2個白球;丙袋中裝有2個白球。這些球除顏色外都相同。從這3個袋中各隨機(jī)地取出1個球。
(1)取出的3個球恰好是2個紅球和1個白球的概率是多少?
(2)取出的3個球全是白球的概率是多少?
分析:根據(jù)題意涉及3個口袋,要能層次分明地表示每次取球的步驟,選擇用畫樹狀圖的方法,列舉所有可能性的結(jié)果,而后根據(jù)樹狀圖來解決問題。
解:(1)畫樹狀圖

根據(jù)樹狀圖可知,所有可能出現(xiàn)的結(jié)果共12種,取出的3個球恰好是2個紅球和1個白球的可能有2種,概率是 。
(2)根據(jù)樹狀圖可知,取出的3個球全是白球的可能有4種,概率是 。


