基于自適應最稀疏時頻分析的結構損傷檢測方法

楊 斌，程軍圣

(湖南大學汽車車身先進設計制造國家重點實驗室，湖南 長沙410082)

基于自適應最稀疏時頻分析的結構損傷檢測方法

楊 斌，程軍圣

(湖南大學汽車車身先進設計制造國家重點實驗室，湖南 長沙410082)

研究了一種新的自適應時頻分析方法——自適應最稀疏時頻分析(ASTFA)方法，并將其運用于結構振動響應分析，提出了基于ASTFA的結構損傷檢測方法。ASTFA方法在EMD方法和壓縮感知的基礎上，建立包含所有IMF分量的過完備字典，通過尋找原信號的最稀疏表示，將信號分解問題轉化為非線性優化問題，在目標優化的過程中實現信號的自適應分解，并直接得到各個分量的瞬時頻率和瞬時幅值。在介紹ASTFA的基礎上，對ASTFA和EMD進行了對比，結果表明了ASTFA方法的優越性。利用ASTFA方法識別了結構的模態參數，提出了基于分量信號瞬時頻率和瞬時能量的損傷指標，對結構損傷進行了檢測。對實際信號的分析結果表明，ASTFA方法可以有效地應用于結構損傷檢測。

結構損傷；自適應最稀疏時頻分析；模態參數識別；瞬時頻率；瞬時能量

引 言

傳統的結構損傷檢測方法主要通過對比損傷前后結構參數的變化對結構工作狀態進行判斷，但這類方法不適用于激勵未知的情況，且無法用于結構響應為非平穩信號情況下的損傷檢測。通過應用現代信號方法，直接對結構振動響應進行分析，提取損傷敏感參數，可以對激勵未知情況下的結構損傷進行檢測，有效克服傳統損傷檢測方法的不足。目前廣泛應用于結構振動響應分析和損傷檢測中的是自適應信號分解方法，典型方法如經驗模態分解(Empirical mode decomposition，EMD)、局部均值分解(Local mean decomposition，LMD)等。Xu［1］等利用EMD方法識別損傷引起的剛度變化，對剪切建筑結構的損傷發生時間和損傷位置進行了檢測。Chen［2］等對機翼翼盒結構的振動響應進行EMD分解，提出了基于第一個內稟模態函數(Intrinsic mode functions，IMF)分量的瞬時能量為損傷指標的損傷檢測方法。Li［3］等進一步結合EMD方法和小波分析方法，首先對振動響應進行EMD分解，然后利用小波分析對IMF分量進行分析，對結構的損傷位置和損 傷 程度 進 行了 檢 測。程軍 圣［4］等 將LMD方法應用到齒輪損傷模式識別中，對齒輪實驗振動信號進行了分析。EMD和LMD都屬于非參數化自適應信號分解方法，都是基于信號極值點的局部特征尺度參數，通過多次迭代獲得瞬時頻率具有物理意義的單分量信號。因此都具有一些共同的不足，如端點效應、模態混淆以及所得到的單分量信號是否具有物理意義缺乏嚴格的數學證明等問題。

THOMAS Y HOU在EMD方法和壓縮感知的基礎上，提出了一種自適應最稀疏時頻分析(A-daptive and sparsest time-frequency analysis，簡稱ASTFA)方法［5］。該算法的主要特點為，在EMD的基礎上，建立包含所有IMF分量的過完備字典，通過尋找原信號的最稀疏表示，將信號分解問題轉化為非線性優化問題。在求解優化問題的過程中，采用傅里葉變化求解最小二乘問題，能快速有效地得到分解結果。該方法通過優化算法求解分量信號，具有嚴格的數學基礎；在目標優化的過程中實現信號的自適應分解，并直接得到各個分量的瞬時頻率和瞬時幅值。本文在介紹ASTFA方法的基礎上，研究了ASTFA方法在結構振動響應分析中的應用，將ASTFA方法與EMD方法進行了對比。同時，將ASTFA方法應用到結構損傷檢測中，通過ASTFA方法分解得到的IMF分量識別結構模態參數，識別損傷前后結構模態參數的變化，并利用分量信號計算損傷指標，對結構損傷進行了檢測。對實際信號的分析結果表明，ASTFA方法可以有效地應用于結構損傷檢測。

1 自適應最稀疏時頻分析方法

1.1 過完備字典的建立

對于信號s(t)，可以通過EMD方法分解為N個IMF分量

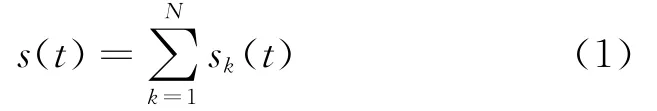
定義包含所有IMF分量的過完備字典［6］

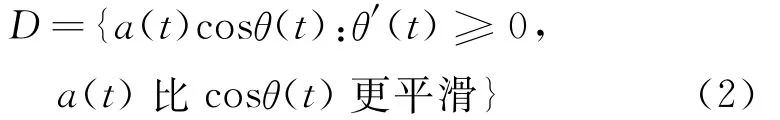
設V(θ)為包含所有a(t)的集合

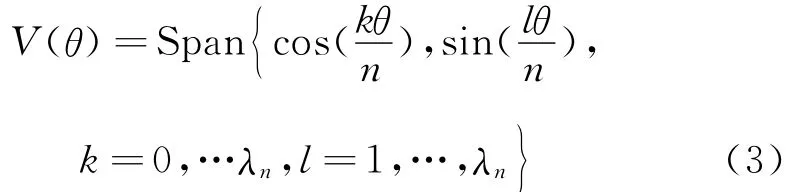
式中 λ≤1/2，n=(θ(1)-θ(0))/(2π)，通過λ可以控制V(θ)的平滑度。

綜上可知，過完備字典定義為

由于D為過完備字典，因此通過該字典對信號進行分解的結果并不唯一，可以得到多種分解結果。為了從這些分解結果中找到最優的分解過程，結合稀疏分解的思想，以得到的分量最少為目標，轉化為最優化問題。

1.2 最優化問題

為了從過完備字典中找到信號的最稀疏表示，以分解得到的分量最少為優化目標，定義如下非線性優化問題：

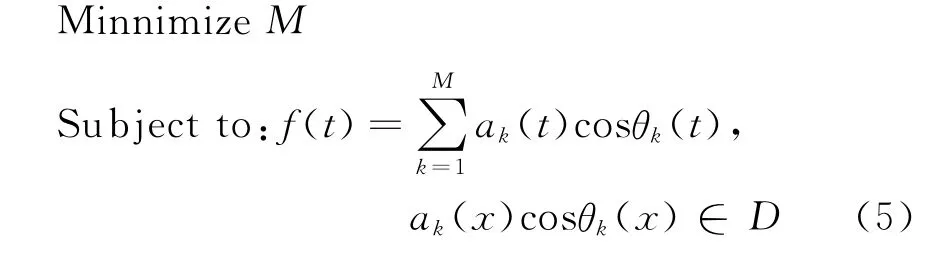
稀疏信號分解可以通過匹配追蹤、基追蹤、框架方法、最佳正交基方法等算法進行求解［7］。其中，匹配追蹤方法最為常用。匹配追蹤方法在迭代過程中，通過將殘余信號向過完備字典庫投影，得到信號的最佳稀疏表示。計算步驟如下：

1)令初始殘差r0等于原函數f(t)，r0=f(t)；

2)求解以下非線性最小二乘問題：

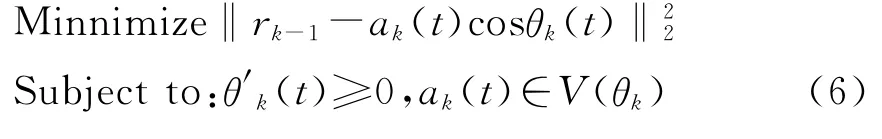
3)更新殘差：rk=f(t)

4)如果‖rk‖2＜ξ0，迭代終止，否則返回1)。

在上述優化問題中，需要步驟2)中的非線性最小二乘問題進行求解，這里采用高斯-牛頓法進行計算，計算步驟如下：

1)選擇θk(0)=θ(0)；

2)求解以下最小二乘問題：

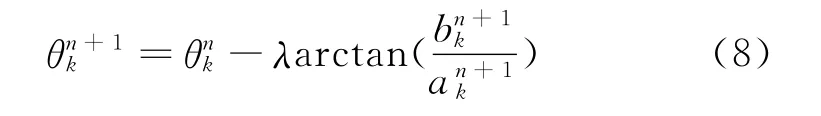
其中，λ∈［0，1］，保證θn+1k為單調增加，定義

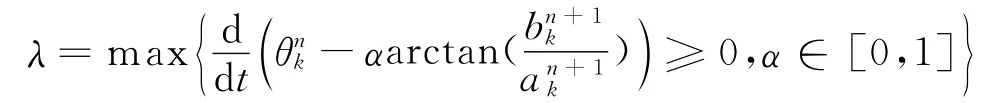
4)若‖θn+1k-θnk‖2＜ξ0，迭代終止，否則返回1)。

由式(7)可知，每次迭代中都需要求解該最小二乘問題，當數據量較大時，計算耗費的時間很長。

由于在每個迭代步中，都要求解最小二乘問題以獲得系數an+1k和bn+1k，在數據長度較大時，計算所耗費的時間很長。引入一種基于快速傅里葉變換(Fast Fourier Transform，簡稱FFT)的算法［6］，可以快速有效地求解得到系數an+1k和bn+1k。

基于快速傅里葉變化的迭代算法計算步驟下：1)選擇初值θ0k=θ0。

2)將r(t)通過插值變換到θn坐標，得到rθn(θnj)

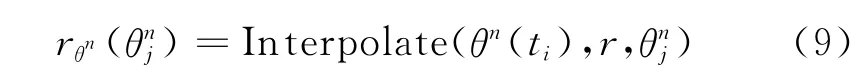
其中，θnj，j=1，…，N為θn坐標的坐標系。

3)通過快速傅里葉變化求得θn坐標下的系數：

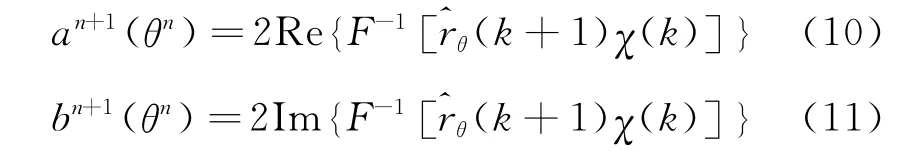
如上所述，χ(k)為一低通濾波器，該濾波器的特性主要由V(t)決定。本文定義χ(k)為如下形式

4)將an+1(θn)和bn+1(θn)插值回原坐標：

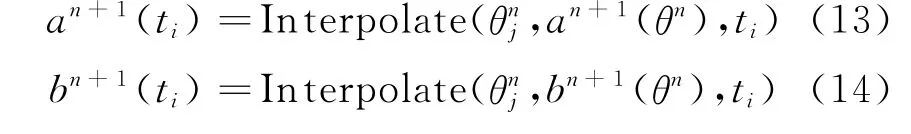
5)更新θn(t)

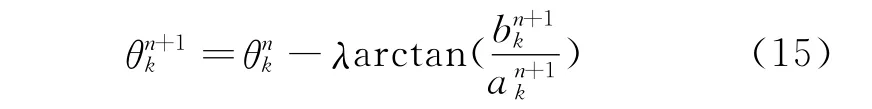
其中，λ∈［0，1］，保證θn+1k為單調增加。

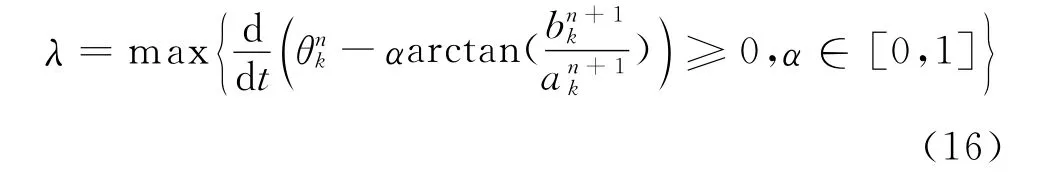
6)若‖θn+1k-θnk‖2＜ξ0，迭代終止，得到第一個IMF分量。否則返回1)。

2 基于自適應最稀疏時頻分析方法的損傷特征提取方法

多自由度系統的運動方程為：

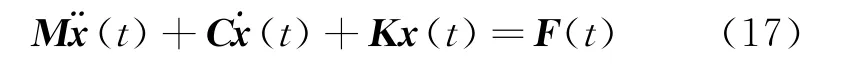
式中 M，C，K分別為系統的質量矩陣、阻尼矩陣和剛度矩陣；x(t)和F(t)分別位移和激振力。

由模態理論可知，當激勵位置為j時，系統在測點i處的響應可以表示為各階模態響應的疊加

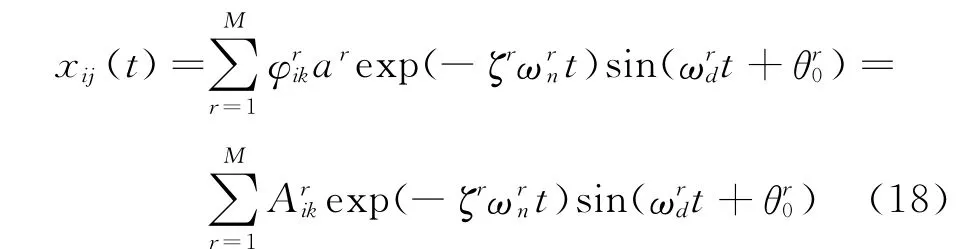
結合ASTFA方法，可以自適應的將多自由度振動信號分解為一系列單模態信號，并可以在求解分量信號的過程中直接求得分量信號的瞬時頻率f(t)和瞬時幅值a(t)。結合式(18)，有

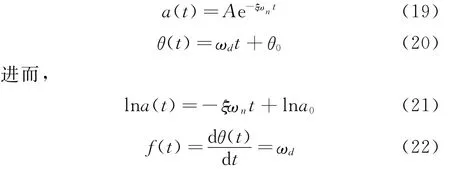
由式(21)和式(22)可知，瞬時相位θ(t)直線方程的斜率對應為阻尼固有頻率ωd，而通過對數-瞬時幅值方程可以求得ξωn，進而可以求得模態參數ωn和ξ。

由式(18)可知，結構響應與模態參數緊密相關，在同一激勵下，損傷帶來的結構參數變化會引起結構振動響應的改變。因此，可以通過結構振動響應提取損傷指標，對結構損傷進行檢測。但不同的損傷模式對結構響應的影響程度不同，如剛度減少的損傷引起的振動響應改變通常表現為低頻模態響應的改變，而裂紋閉合引起的振動響應的變化通常表現在高頻范圍。在實際應用中，大多無法事先對結構的損傷模式進行預測或者初步判斷，因此有必要對基于振動響應的損傷特征提取方法進行研究，提取有效的損傷指標。

通過ASTFA方法分解得到的IMF分量提取損傷指標。利用ASTFA方法可以將結構振動響應分解為一系列單模態響應，這里定義分量信號的瞬時頻率和瞬時能量之和作為損傷指標

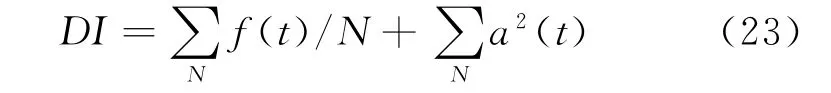
式中 f(t)為分量信號的瞬時頻率，a(t)為分量信號的瞬時幅值，可以通過ASTFA方法直接獲得。該損傷指標從信號的振動頻率和振動能量出發，描述了系統的振動特性。不同的損傷類型對各IMF分量的影響程度不同，因此需要選擇合適的IMF分量。通過余弦相似度來描述向量之間的相似性，向量A和B之間的余弦相似度定義如下，

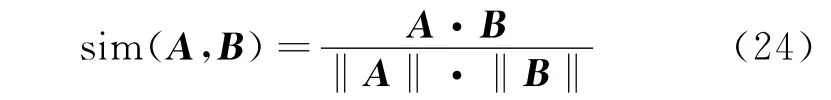
根據式(24)計算損傷前后各IMF分量之間的相關性，選擇相關性最小的IMF分量，計算損傷指標。

3 仿真信號分析

ASTFA方法在EMD方法的基礎上，選擇IMF分量作為基函數，通過優化方法獲取IMF分量。既與EMD方法緊密聯系，又與其存在本質區別。

為了對比ASTFA方法與EMD方法的分解能力，取四自由度系統的脈沖響應進行數值仿真。系統參數為：A(1)=5，A(2)=20，A(3)=10，A(4)=15；ξ(1)=0.023 3，ξ(2)=0.018 0，ξ(3)=0.004 2，ξ(4)=0.010 9；ω(1)n=15.004 1，ω(2)n=30.004 9，ω(3)n=45.000 4，ω(4)n=60.003 5；θ(1)=0，θ(2)=0，θ(3)=0，θ(4)=0。其時域波形如圖1所示。

在不對端點進行處理的情況下，分別采用ASTFA方法和EMD方法對仿真響應信號進行分析。ASTFA方法可以將仿真信號有效地分解為4個具有物理意義的IMF分量，分解結果如圖2所示。而EMD方法分解得到的結果存在較為明顯的模態混淆現象，分解結果如圖3所示。這主要是由于EMD方法缺乏嚴格的數學推導過程，隨著信號分量的增加，迭代過程中容易受到上下包絡精度及噪聲等的影響，分解得到的IMF分量會出現同一頻率成分被分解到相鄰的IMF中。

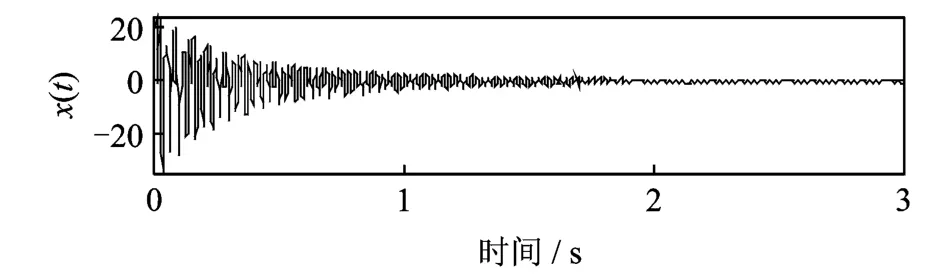
圖1 仿真信號Fig.1 The simulation signal x(t)

圖2 仿真信號的ASTFA分解結果Fig.2 The decomposed signal of x(t)using ASTFA

為了進一步對比ASTFA方法和EMD方法分解結果，分別計算各IMF分量與理論值之間的相似性和能量變化率。通過余弦相似度來描述IMF分量與理論值之間的相似性，并進一步定義能量變化率為

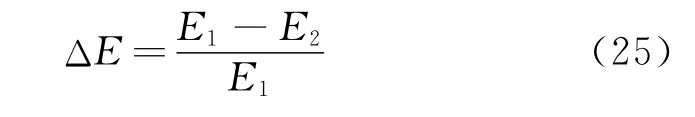
計算結果如表1所示。由表1可知，ASTFA方法的分解結果與理論值存在較為理想的相關性，能量變化率由于端點效應的影響，存在較為明顯的偏差，但仍在正常范圍內。而EMD方法分解得到的分量與理論值的相關性較差，且能量變化率更為明顯，與原信號存在較大的偏差。

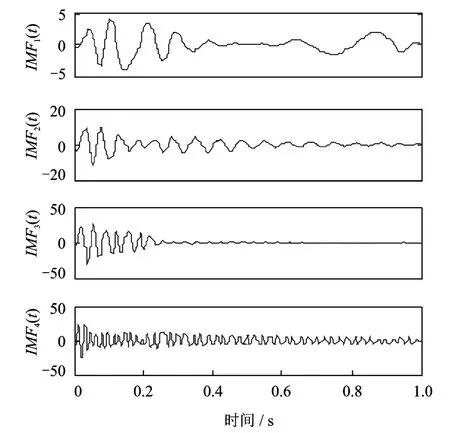
圖3 仿真信號x(t)的EMD分解結果Fig.3 The decomposed signal of x(t)using EMD

表1 ASTFA方法與EMD方法分解結果對比Tab.1 The comparison of the decomposing results between the ASTFAand the EMD

由分解結果可知，ASTFA方法分解得到的IMF分量存在端點效應。為了得到更準確的IMF分量，以便對模態參數進行精確的識別，對仿真信號進行了鏡像延拓，采用ASTFA方法的分解結果如圖4所示。分解得到的各IMF分量的瞬時幅值和瞬時頻率也在分解過程中直接得到，如圖5和6所示。

對鏡像延拓后的信號進行EMD分解，得到的IMF分量如圖7所示。進一步對EMD分解后得到的IMF分量進行Hilbert變換，計算得到瞬時幅值和瞬時頻率，結果如圖8和9所示。

如圖所示，ASTFA方法分解結果較為理想，得到的瞬時幅值曲線光滑，且較為準確地反映了原信號的特性，瞬時幅值也較為準確地反映了結構的振動特性。而EMD方法的分解結果不準確，瞬時幅值出現了較為明顯的偏差和波動，而且瞬時頻率也不能準確地反映結構特性。

由上可知，ASTFA方法在對結構振動響應進行分析時，要優于EMD方法。主要表現在：

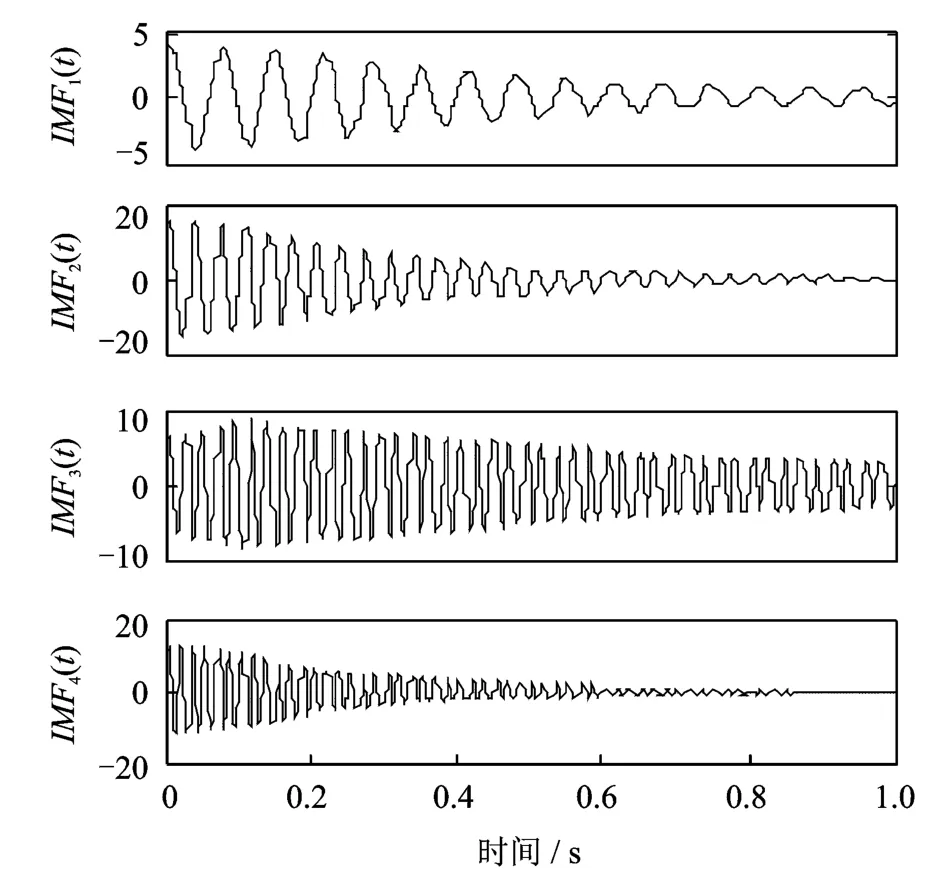
圖4 鏡像延拓后的ASTFA分解結果Fig.4 The decomposed signal using ASTFAafter the mirror extension

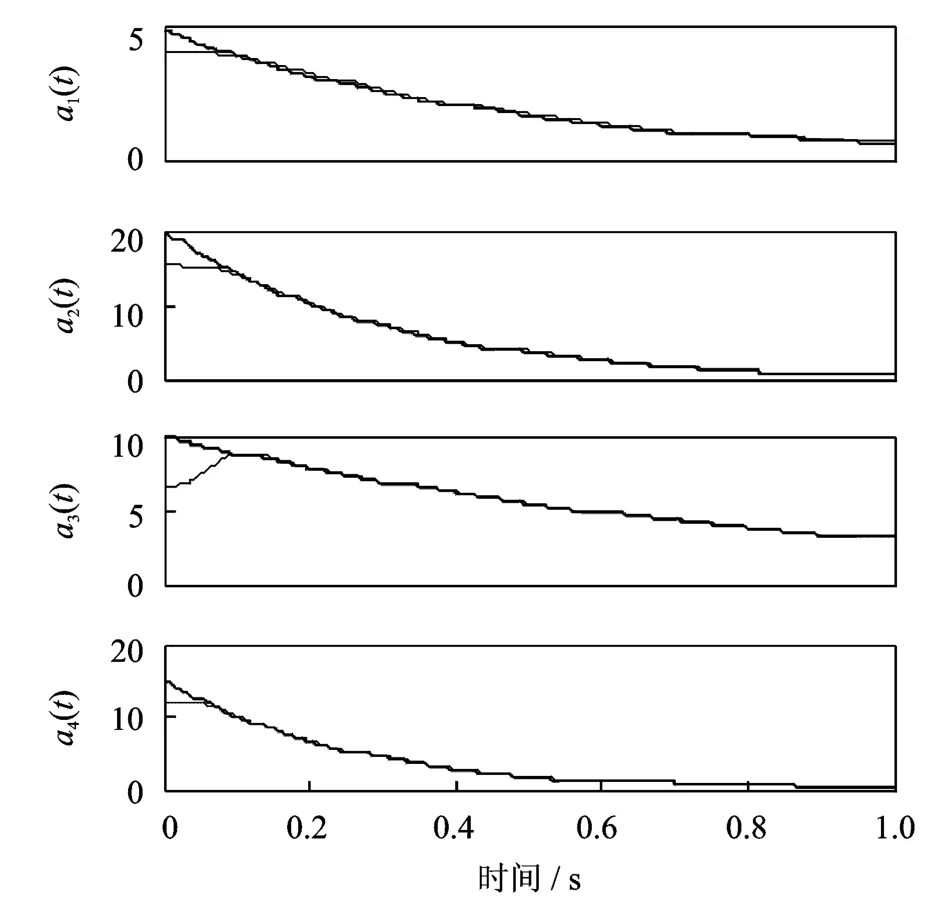
圖5 鏡像延拓后由ASTFA方法得到的各IMF分量的瞬時幅值Fig.5 The instantaneous amplitude of the IMFs using ASTFAafter the mirror extension

1)ASTFA方法具有嚴格的數學基礎，在目標優化的過程中實現信號的自適應分解，能準確地得到分量信號，避免了模態混淆。

2)ASTFA方法在求解非線性問題的過程中，能直接得到分量信號的瞬時幅值和瞬時頻率，不需要對分量信號進行Hilbert變換，避免了Hilbert變換帶來的邊緣誤差及負頻率等問題。

結合式(21)和式(22)利用ASTFA方法分解得到的IMF分量識別結構的模態參數，如表2所示。

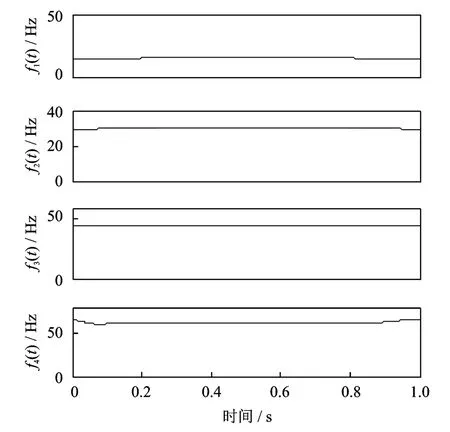
圖6 鏡像延拓后由ASTFA方法得到的各IMF分量的瞬時頻率Fig.6 The instantaneous frequency of the IMFs using ASTFAafter the mirror extension

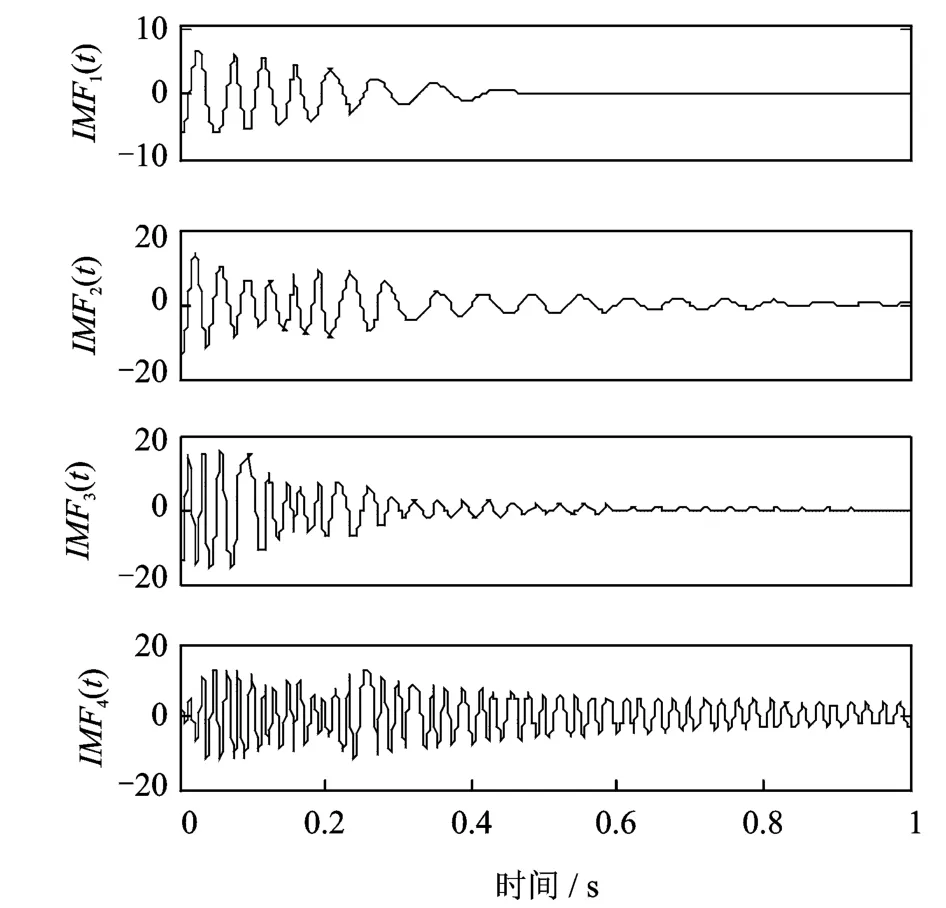
圖7 鏡像延拓后由EMD方法的分解結果Fig.7 The decomposed signal using EMD after the mirror extension

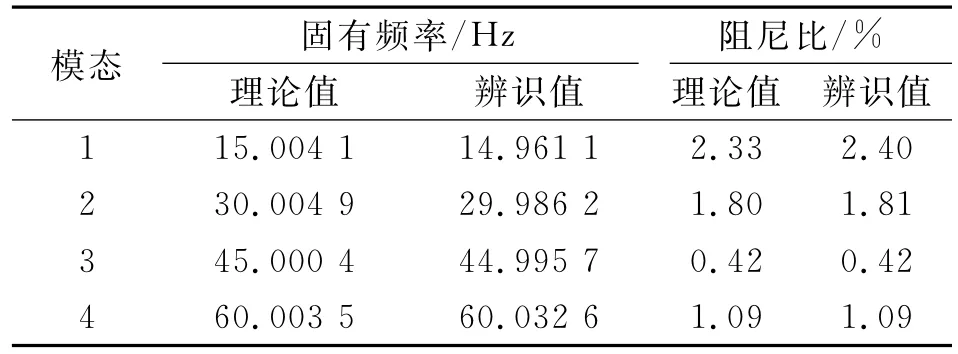
表2 模態參數識別結果Tab.2 The estimation results of modal parameters

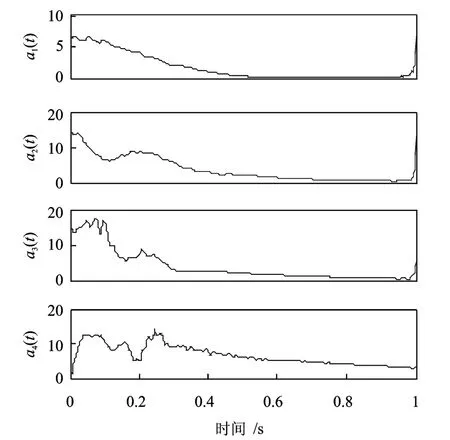
圖8 鏡像延拓后由EMD方法得到的各IMF分量的瞬時幅值Fig.8 The instantaneous amplitude of the IMFs using EMD after the mirror extension

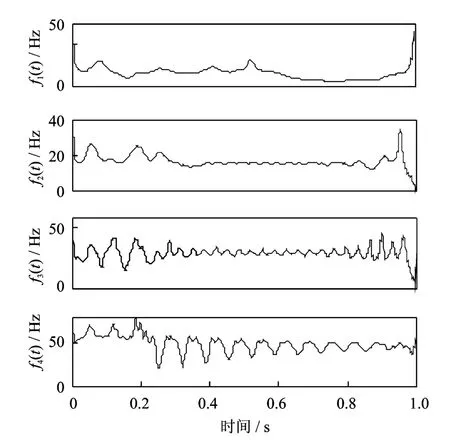
圖9 鏡像延拓后由EMD方法得到的各IMF分量的瞬時頻率Fig.9 The instantaneous frequency of the IMFs using EMD after the mirror extension

4 實驗驗證

4.1 IASC-ASCE結構健康監測基準算例

該基準結構由IASC-ASCE提出［8］，在結構損傷識別方法研究中得到廣泛應用［9，10］。該結構分為4層，為2×2跨的鋼框架縮尺模型，模型平面尺寸為2.5 m×2.5 m，每層高度為0.9 m，每層連接可以自由拆卸的8根斜支撐。該結構的有限元模型如圖10所示，采用12自由度的有限元模型獲取結構振動響應，該模型保留每層中心節點的兩個平動自由度(x，y)和一個轉動自由度θz。考慮兩種損傷模式：1)去掉第一層所有斜支撐；2)去掉第一層和第三層所有斜支撐。為了獲取結構在不同工作狀態下的振動響應，對結構施加白噪聲激勵，激勵位置為頂板中心，采樣頻率設置為1 000 Hz，時長為100 s。

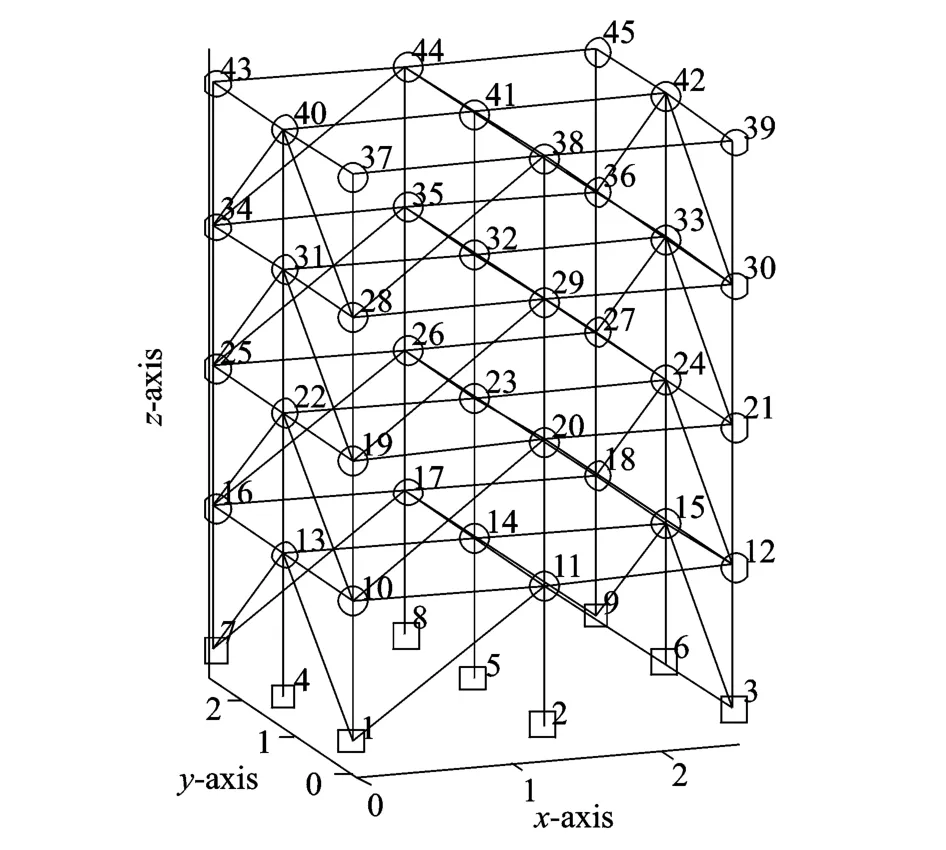
圖10 ASCE Benchmark結構有限元模型Fig.10 The FEMmodel of the ASCE Benchmark structure

由自然激勵技術(Natural Excitation Technique，NEx T)原理可知，白噪聲激勵下結構的互相關函數與脈沖響應函數具有相同的形式［11］，而通常互相關函數可由互功率譜函數進行反傅里葉變換可求得。選擇參考點為第四層的節點43，計算其與第一層節點12的互功率譜。如圖11所示為互功率譜及響應的互相關函數。

求得的互相關函數即為結構在節點12處的脈沖響應函數，應用ASTFA方法將其分解為一系列的IMF分量，并根據式(21)和式(22)求解結構的模態參數，結果如表3和圖12所示。由圖12可知，不同損傷模式下計算得到的固有頻率不同，且隨著損傷程度的增加，固有頻率逐漸減小。

利用ASTFA方法對振動響應進行分解，根據式(23)計算損傷指標，結果如圖13所示。由圖13可知，各IMF分量所計算得到的損傷指標對損傷的敏感程度不同，因此需要選擇合適的IMF分量，才能保證損傷檢測的準確性。根據式(24)計算損傷前后各IMF分量之間的相關性，選擇相關性最小的IMF分量，計算損傷指標。這里選擇第二個分量信號IMF2，結果如圖14所示。由圖14可知，通過選擇ASTFA方法獲得的IMF分量，選擇合適的IMF分量計算損傷指標，可以有效對結構的工作狀態進行判斷。

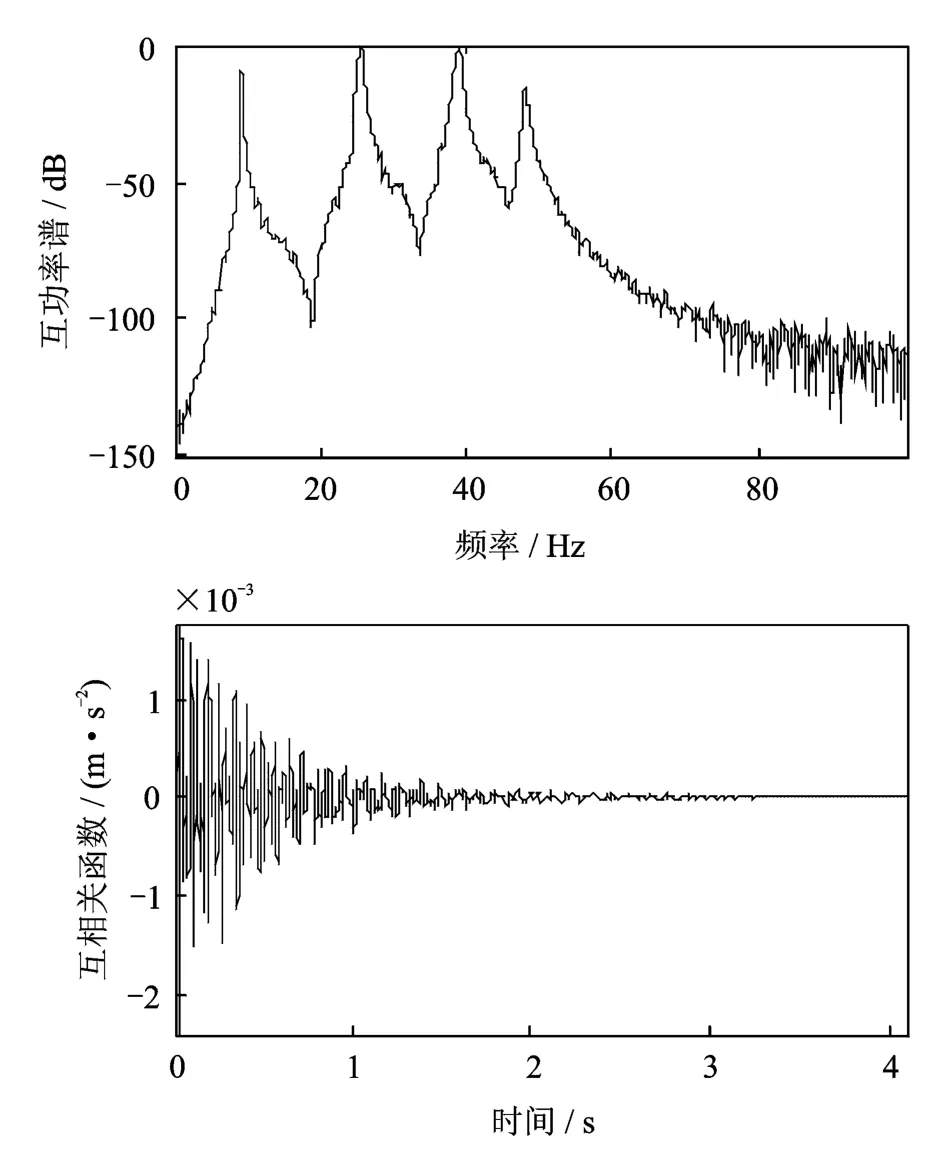
圖11 正常狀態下結構的互功率譜和互相關函數Fig.11 The cross power spectrum and the cross correlation function of the structure under normal condition

圖12 結構在不同工作狀態下的模態參數Fig.12 The modal parameters of the structure under different conditions

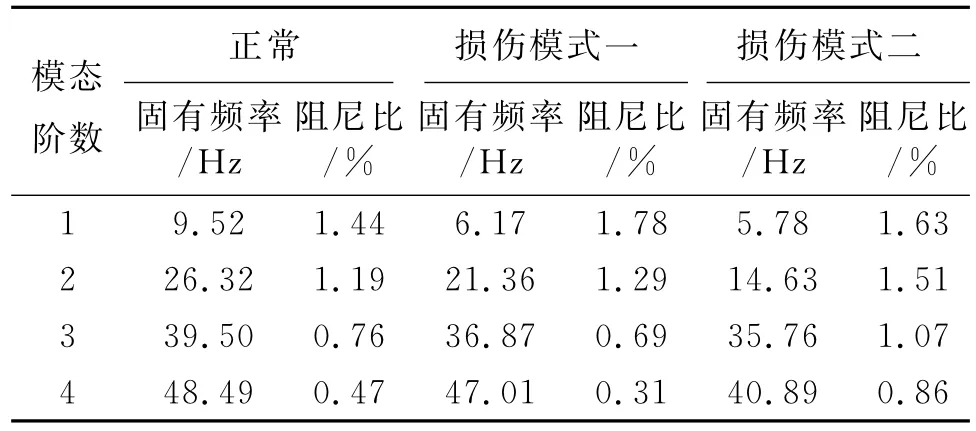
表3 ASCE Benchmark結構在不同工作狀態下的模態參數Tab.3 The modal parameters of the ASCE Benchmark structure under different conditions

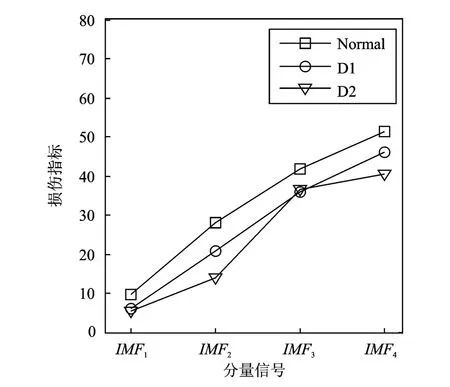
圖13 ASTFA方法分解后各IMF分量的損傷指標Fig.13 The damage index of each IMFusing ASTFA

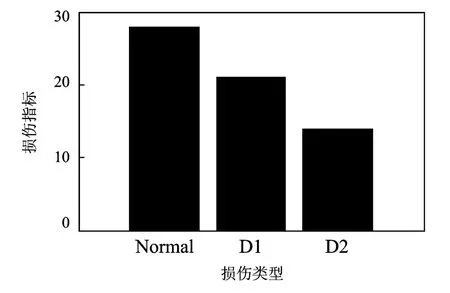
圖14 ASTFA方法分解后IMF2分量的損傷指標Fig.14 The damage index of IMF2using ASTFA

4.2 自由梁實驗

實驗對不同損傷類型的自由梁進行錘擊測試，采集振動加速度信號。實驗中對梁兩端通過彈簧進行吊裝，來模擬垂直方向的自由狀態，如圖15所示。自由梁結構示意圖如圖16所示，自由梁尺寸為(1 300×30×30 mm3)，共安裝7個振動加速度傳感器，編號從左到右分別為①～⑦，錘擊位置為A。通過LMS SCADAS數據采集前端進行測試，實驗中設置采樣頻率為2 048 Hz，采樣時間為8 s。通過對自由梁不同位置切割槽來模擬損傷，損傷設置如表4所示，其中損傷模式D2為在自由梁設置2個不同位置的損傷。

圖15 自由梁實驗Fig.15 The free beam experiment

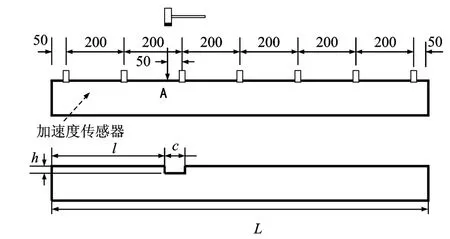
圖16 自由梁結構實驗示意圖(單位：mm)Fig.16 The free beam structure(Unit：mm)

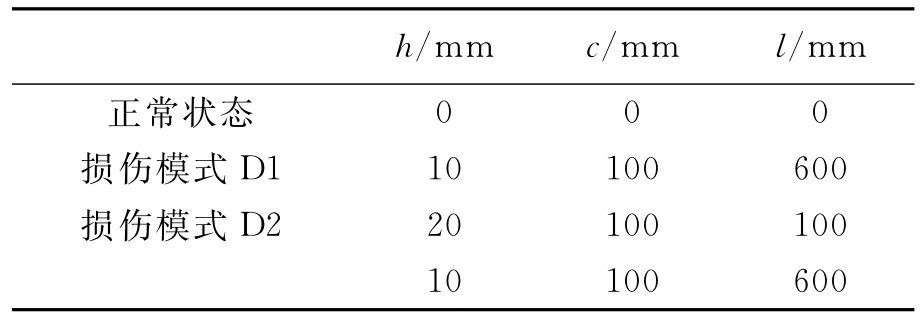
表4 3種結構工作狀態Tab.4 The three different working conditions of the beam

對自由梁各點的振動響應進行ASTFA分析，如圖17所示為正常狀態下測點1處的IMF分量。進一步利用式(21)和式(22)對不同損傷狀態下的結構模態參數進行識別，并與LMS Test.Lab中的最小二乘復指數法(Least Square Complex Exponential method，LSCE)方法的模態參數識別結果進行了對比，結果如表5所示。由表5可知，通過ASTFA方法可以準確地將振動響應分解為單模態響應，得到準確的固有頻率值；而阻尼比的辨識結果受到實驗中的噪聲以及測試誤差的影響，辨識結果準確度有所下降，辨識精度仍需提高。

通過圖18可以對比不同損傷類型下結構的固有頻率的變化情況。可知當結構存在不同模式的損傷時，其模態參數發生了較為明顯的變化，隨著損傷程度的增加，固有頻率逐漸減小。

對測點1處的不同損傷類型下的振動響應通過ASTFA方法進行分解，根據式(24)計算損傷前后各IMF分量之間的相關性，選擇相關性最小的IMF分量，根據式(23)計算損傷指標，結果如圖19。由圖19可知，通過ASTFA方法獲得結構響應的分量信號，進一步選擇合適的IMF分量計算損傷指標，可以有效地對結構損傷進行檢測。

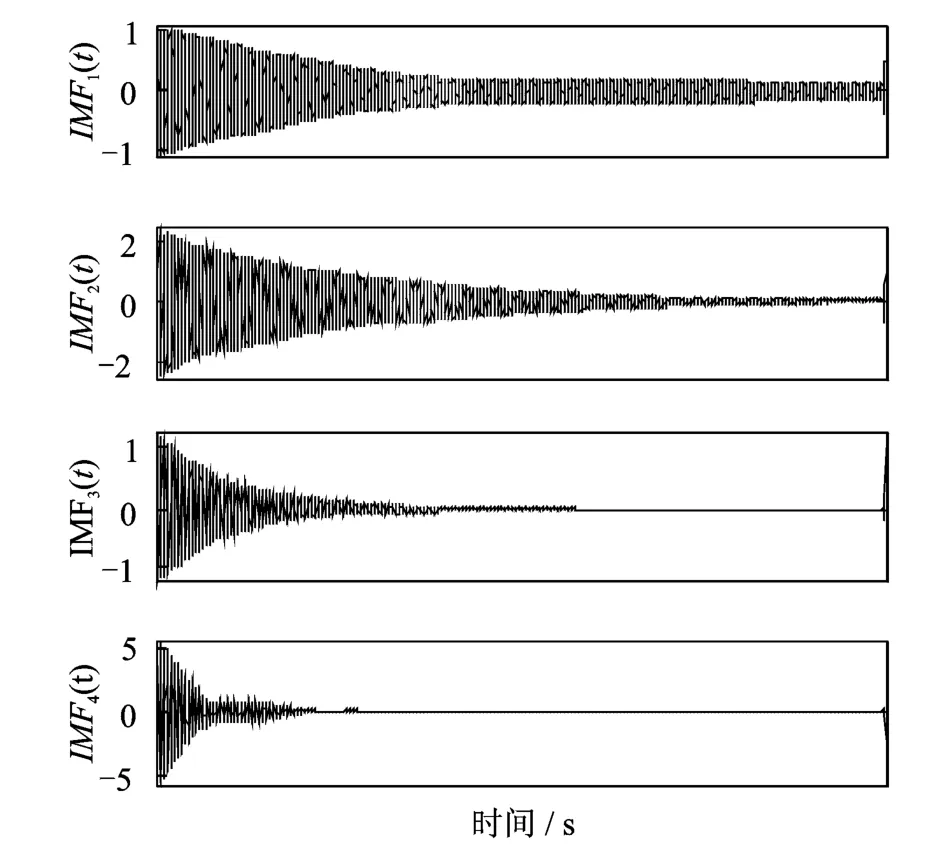
圖17 正常狀態下測點1處分解得到的IMF分量Fig.17 The obtained IMFs of sensor 1 under normal condition

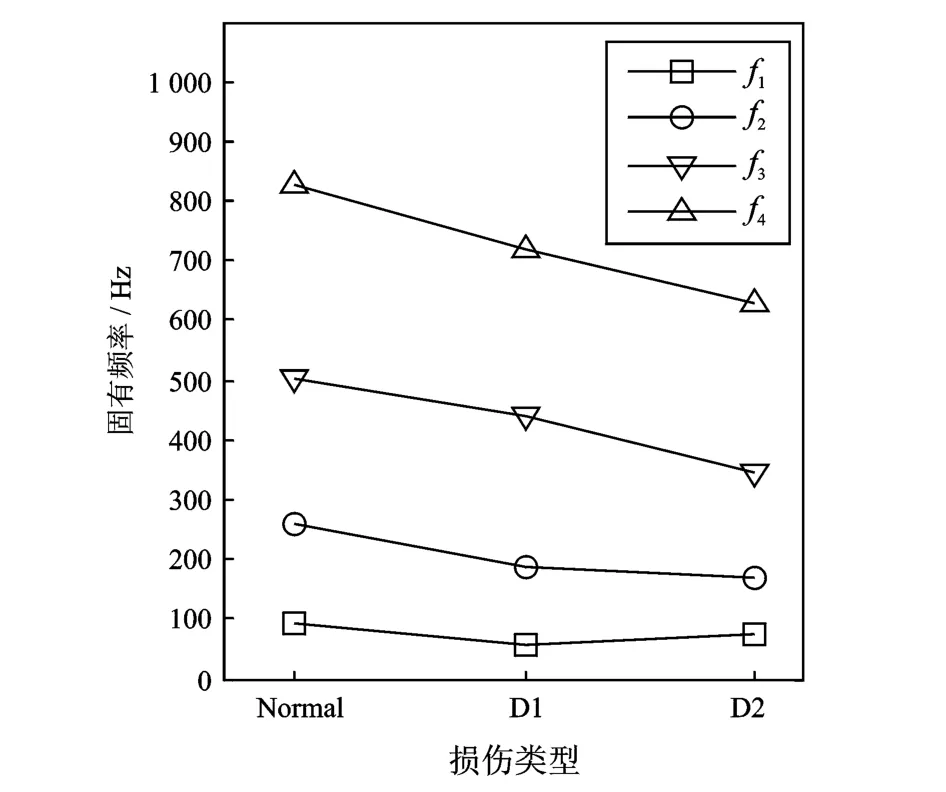
圖18 自由梁結構在不同工作狀態下的模態參數Fig.18 The modal parameters of the free beam under different working conditions

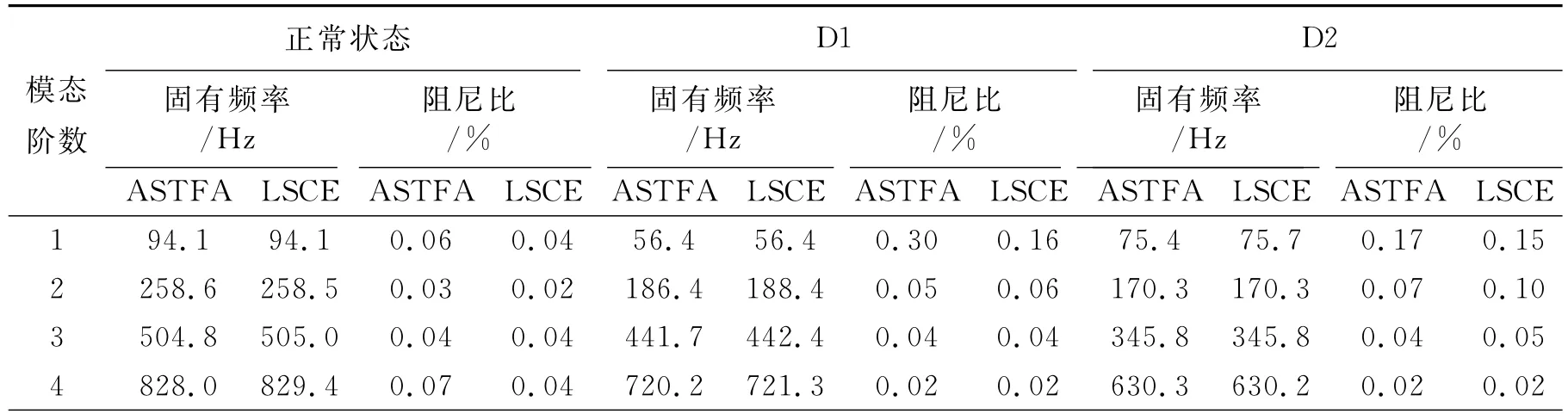
表5 自由梁結構在不同工作狀態下的模態參數Tab.5 The modal parameters of the free beam under different working conditions

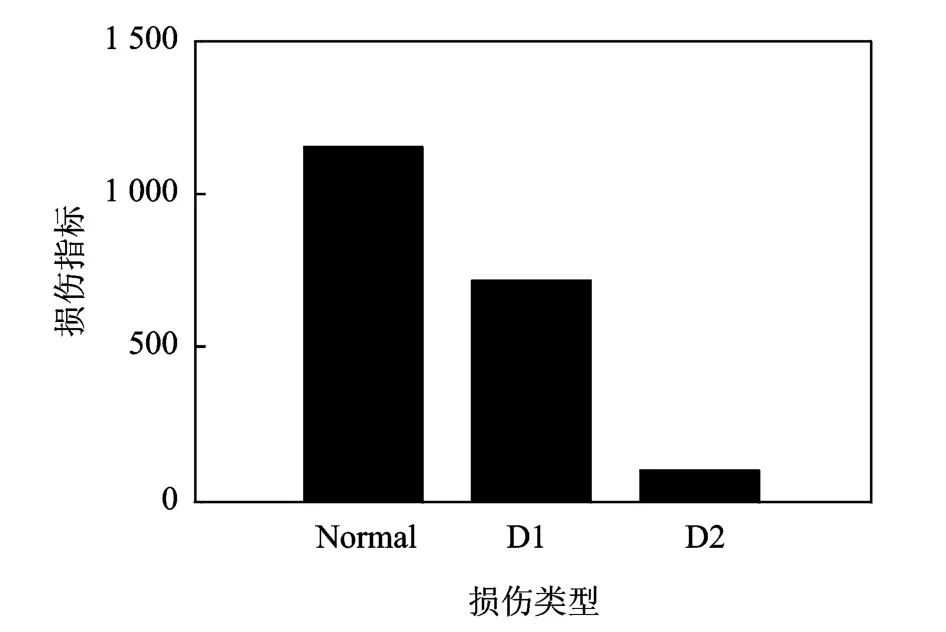
圖19 ASTFA方法分解后IMF2分量的損傷指標Fig19 The damage index of IMF2using ASTFA

5 結 論

自適應最稀疏時頻分析方法為一種新穎的時頻分析方法，其主要特點在于通過優化算法求解分量信號，具有嚴格的數學基礎；在目標優化的過程中實現信號的自適應分解，并直接得到各個分量的瞬時頻率和瞬時幅值。該方法在EMD方法的基礎上建立過完備字典，通過尋找原信號的最稀疏表示，將信號分解問題轉化為非線性優化問題。這也從根本上克服了EMD方法的模態混淆及過包絡等問題，通過仿真信號的分析也表明ASTFA方法的分解結果要優于EMD方法。同時，ASTFA方法在計算過程中需要對最小二乘問題進行求解，往往耗費大量的計算時間，雖然現有方法通過FFT算法可以有效提高計算效率，但基于FFT方法的ASTFA方法適合處理周期信號，在處理非周期信號時較難收斂，且容易產生計算誤差。此外，ASTFA方法存在較為明顯的端點效應，對計算精度產生影響，這些都需要在以后的研究中加以克服。

通過ASTFA方法可以將結構振動信號分解為單模態響應，從而準確地識別結構的模態參數，并提取損傷參數，可以應用于結構損傷檢測。通過對ASCE Benchmark結構及自由梁實驗結構的分析，可知通過ASTFA方法可以有效對結構的工作狀態進行檢測。同時，本文提出的方法能對結構的損傷進行檢測，但無法進一步對結構的損傷位置及損傷程度進行識別。因此，有必要在ASTFA方法的基礎上，提出新的有效的損傷指標，進一步對微小損傷以及結構的損傷位置進行識別，這也是將來需要進一步研究的內容。

［1］Xu L Y，Chen J.Structural damage detection using empirical mods decomposition：Experimental investigation［J］.Journal of Engineering Mechanics，2004，130(11)：1 279—1 288.

［2］Chen HG，Yan Y J，Jiang J S.Vibration-based damage detection in composite wingbox structures by HHT［J］.Mechanical Systems and Signal Processing，2007，21(1)：307—321.

［3］Li Helong，Deng Xiaoyan，Dai Hongliang.Structural damage detection using the combination method of EMD and wavelet analysis［J］.Mechanical Systems and Signal Processing，2007，21(1)：298—306.

［4］程軍圣，楊宇，于德介.局部均值分解方法及其在齒輪故障診斷中的應用［J］.振動工程學報，2009，22(1)：76—84.Cheng Junsheng，Yang Yu，Yu Dejie.The local mean decomposition method and its application to gear fault diagnosis［J］.Journal of Vibration Engineering，2009，22(1)：76—84.

［5］Thomas Y H，Shi Zuoqiang.Adaptive data analysis via sparse time-frequency representation［J］.Advances in Adaptive Data Analysis，2011，3(1-2)：1—28.

［6］Thomas Y H，Shi Zuoqiang.Data-driven time-fre-quency analysis［J］.Applied and Computational Harmonic Analysis，2012，25(2)：284—308.

［7］彭富強，于德介，羅潔思，等.基于多尺度線調頻基稀疏信號分解的軸承故障診斷 ［J］.機械工程學報，2010，46(7)：88—95.Peng Fuqiang，Yu Dejie，Luo Jiesi，et al.Sparse signal decomposition method based on multi-scale chirplet and its application to bearing fault diagnosis［J］.Journal of Mechanical Engineering，2010，46(7)：88—95.

［8］Johnson E，Lam HF，Katafygiotis L S，et al.Phase I IASC-ASCE structural health monitoring Benchmark problem using simulated data［J］.Journal of Engineering Mechanics，2004，130(1)：3—15.

［9］Lin Silian，Yang J N，Zhou Li.Damage identification of a Benchmark building for structural health monitoring［J］.Smart materials and structures，2005，14(3)：169—162.

［10］Heung FL，Ching T.N.The selection of pattern features for structural damage detection using an extended Bayesian ANN algorithm［J］.Engineering Structures，2008，30(10)：2 762—2 770.

［11］Juan MC，Shirley J D.Erik AJ.Natural excitation technique and eigensystem realization algorithm for phase I of the IASC-ASCE Benchmark problem：Simulated data［J］.Journal of Engineering Mechanics，2004，130(1)：49—60.

The damage detection method base on the adaptive and sparsest time-frequency analysis

YANG Bin，CHENG Jun-sheng
(State Key Laboratory of Advanced Design and Manufacture for Vehicle Body，Hunan University，Changsha 410082，China)

Aself-adaptive time-frequency analysis method—the adaptive and sparsest time-frequency analysis(ASTFA)and its application to damage detection are studied in the paper.Based on the Empirical Mode Decomposition(EMD)and the compressed sensing theory，the ASTFAmethod translates the signal processing method into a non-linear optimization problem by looking for the sparest decomposition of the signal in the largest possible dictionary consisting of intrinsic mode functions.The adaptive decomposition of the original signal can be obtained through the solution of the optimization problem，and the instantaneous frequency and the instantaneous amplitude can be obtained directly.Then，an comparison is made between the ASTFAmethod and the EMD method to show the superiority of the ASTFA.The modal parameters are estimated and a damage index is proposed based on the instantaneous frequency and the instantaneous energy.The analysis results of the experiments show that the ASTFAmethod can be applied to the structural damage detection.

structural damage detection；the adaptive and sparsest time-frequency analysis；modal parameter estimation；instantaneous frequency；instantaneous energy

O346.5

A

1004-4523(2015)04-0640-10

10.16385/j.cnki.issn.1004-4523.2015.04.018

楊斌(1987—)，男，博士研究生。電話：15111364608；E-mail：yspark@163.com

2014-04-01；

2015-05-06

國家自然科學基金資助項目(51375152)