基于Group MCP Logistic模型的個人信用評價分析

胡小寧 何曉群 馬學俊

摘要：在利用Logistic模型分析個人信用評價問題時，需要進行變量選擇。Group MCP不僅可以將相關變量以組為單位進行變量選擇，還可以對組內變量進行選擇。文章根據個人信貸數據，建立了Group MCP Logistic模型，并與Group Lasso、Group Bridge所得的結果進行比較，綜合考慮模型復雜度和預測正確率，發現根據Group MCP建立的模型效果是最優的。

關鍵詞：Group MCP；Logistic模型；個人信用評價；變量選擇

一、 引言

個人消費信貸在我國迅速發展，對拉動經濟增長起到了一定的促進作用。但其中也隱藏著很大的潛在風險，即信貸資產不能及時有效地收回。因此，急需建立完善的個人信用評價體系，從而降低信貸風險。個人信用評價的核心是建立不同客戶的信用評價模型，根據信用評價模型對信貸申請人進行評分，從而決定是否給予貸款。

個人信用評價分析中，應用最廣泛的方法有統計分析和機器學習兩類，前者在模型穩健性和可解釋性上有很大的優勢。統計分析方法中，學者最關注的是Logistic模型，其計算方法簡單、預測準確率高、變量解釋能力強。但當Logistic模型涉及的變量很多時，直接使用也存在多重共線性和計算復雜度等問題。因此，變量選擇是個人信用評價問題的重點和難點。

傳統的變量選擇方法有最優子集法和逐步回歸法，但這些方法計算量大，且不穩定，當數據有微小變化時，可能得到完全不同的模型，其結果往往是局部最優解，并非全局最優解，尤其當變量個數大于樣本量時，方法失效。Lasso是目前應用廣泛的變量選擇方法，但在個人信用評價問題研究中，許多解釋變量是定性變量，對其進行數量化后引入大量的虛擬變量。在利用最優子集、逐步回歸或Lasso進行變量選擇時，只能選擇某個虛擬變量，而不是將相關的虛擬變量作為整體進行選擇。Group Lasso將相關虛擬變量作為整體進行選擇，使其能夠整體剔除或保留在模型中，但并不能實現對群組內變量的選擇。Group Bridge既可以實現選擇重要的組，也可以選擇這些組里面的重要變量，但其懲罰函數在某些點不可微。Group MCP（Group Minimax Concavepenalty）解決了Group Bridge不可微的問題。

本文將建立基于Group MCP的Logistic模型，對個人信用評價的影響因素進行選擇和分析，并將其與基于Group Lasso、Group Bridge所得的結果進行比較。

二、 Group MCP Logistic模型

三、 實例分析

1. 數據來源。本文數據選用的是德國某銀行的個人信貸數據集合。該數據集中有1 000條記錄，包括21個字段，其中前20個字段為信貸申請人的個人特征描述，最后1個字段是銀行對客戶信用級別的定義：0為“差客戶”，1為“好客戶”。

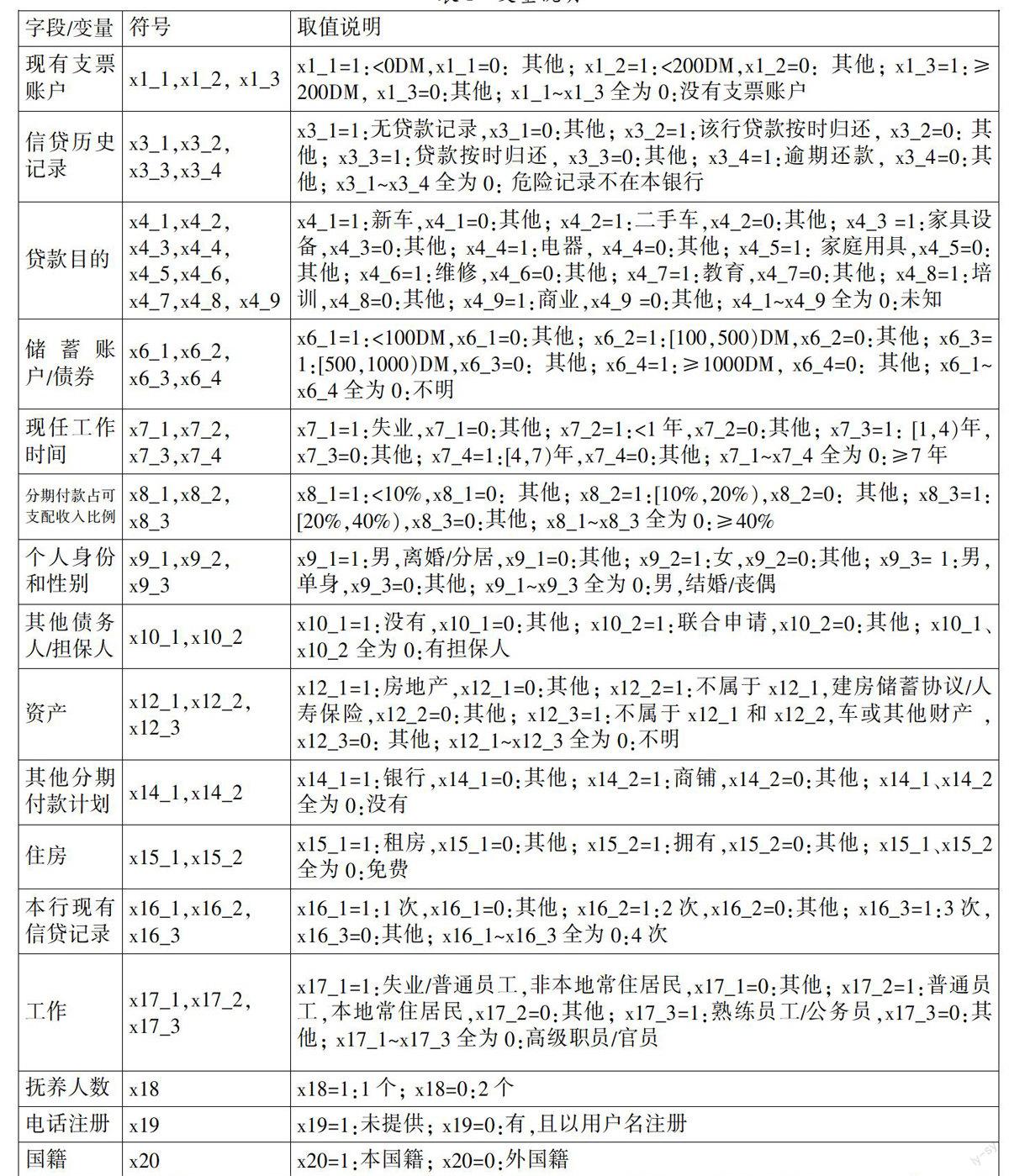
本文所用數據包括21個字段，將其進行處理、編碼后的結果（解釋變量20組共52個，因變量1個）見表1。

原始數據中，信貸期限（x2）、貸款金額（x5）、當前居住地居住時間（x11）、年齡（x13）為連續型數據，為克服量綱的影響，將其標準化處理后再進行分析。

本文所用數據集中，包括700條信用“好客戶”和300條信用“差客戶”，分別從中隨機抽取80%用作訓練集，剩余20%用作測試集。訓練集中信用“差客戶”與“好客戶”的數量比為3：7，數據不平衡比較明顯，為了降低數據不平衡對分析結果造成的影響。采用Random Oversampling方法在信用差客戶中生成120條記錄參與建立模型。

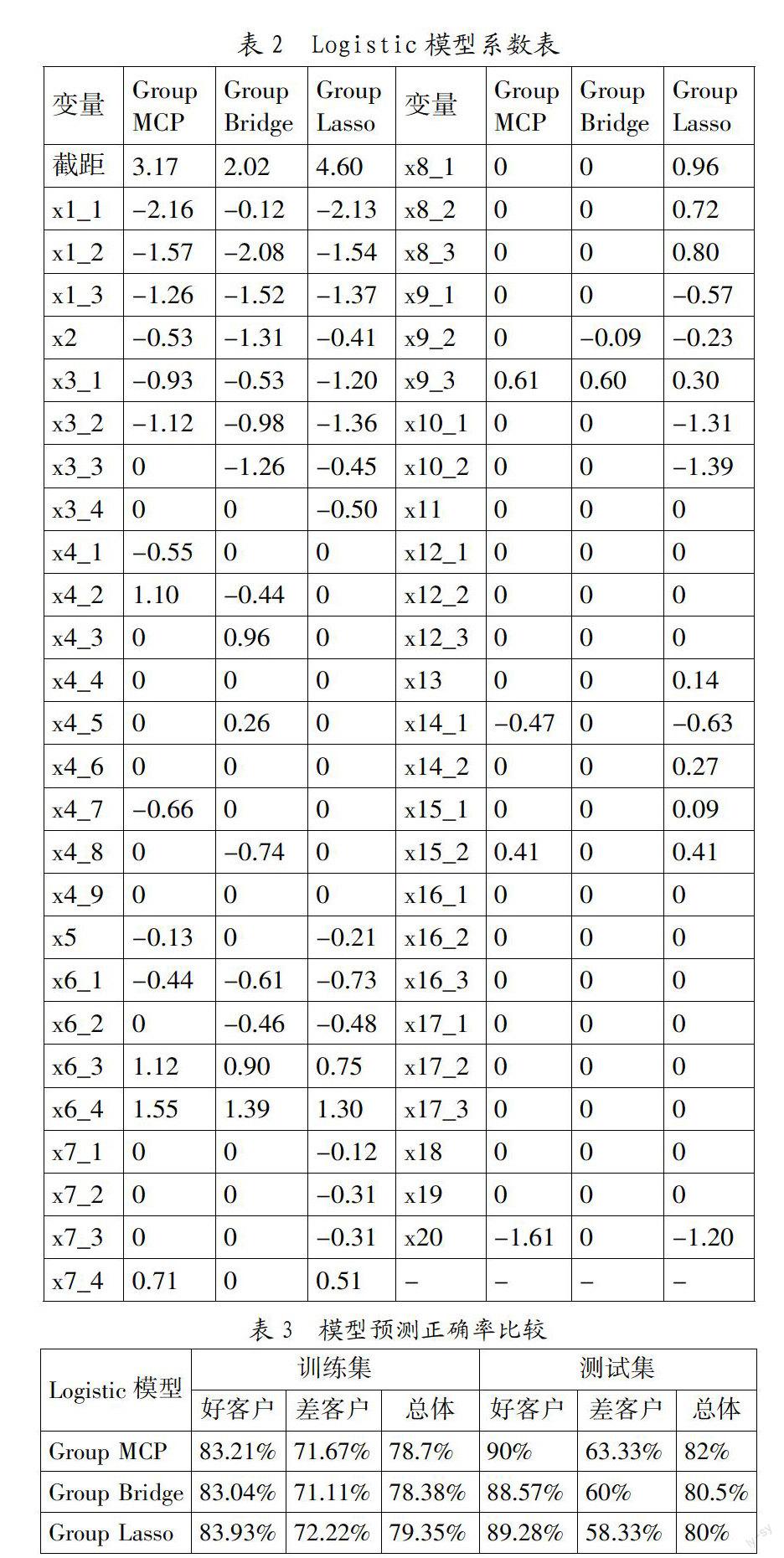
2. Group MCP Logistic模型的建立。本文數據分析通過R軟件的grpreg程序包完成，得到非零解釋變量11組共18個，系數壓縮為零的解釋變量9組共34個，見表2。

由表2可以看出：現有支票賬戶（x1組）額度越高的客戶，違約的概率越小（x1_13. 模型比較。本文還建立了基于Group Lasso和GroupBridge的Logistic模型，其參數估計的結果見表3。

從模型復雜度上來比較：Group Lasso保留了13組共31個變量；Group Bridge保留了7組共17個解釋變量；Group MCP保留了11組共18個變量。Group MCP與Group Lasso相比，保留變量的組數差不多，但變量個數前者比后者大大減少，Group MCP在組內選擇變量的優勢得到體現。Group MCP與Group Bridge相比，保留的變量個數只差1個，但前者比后者保留的組數多了4個，表明Group MCP保留了更多的組信息。

從模型預測正確率上來比較，表3說明，基于Group MCP建立的Logistic模型，在訓練集和測試集上的預測正確率要優于Group Bridge；在訓練集上預測的正確率，Group Lasso要高于Group MCP和Group Bridge，而測試集上的預測正確率，Group MCP要優于Group Lasso，尤其是“差客戶”的預測正確率上提升很大，這可能是由于Group Lasso沒有進行組內變量選擇，從而保留了過多的解釋變量，有一定的過擬合現象。因此，綜合考慮，Group MCP的Logistic模型效果最好。

四、 結論

建立Logistic模型是個人信用評價分析中應用最為廣泛的方法。當解釋變量尤其是虛擬變量過多時，需要進行以組為單位的變量選擇。Group Lasso可以解決組變量的選擇問題，將相關的變量作為組進行整體剔除或保留在模型中，但在組內，不能夠進行變量選擇。Group MCP改進了Group Lasso算法，不僅僅能夠進行組變量選擇，也能在組內淘汰掉不顯著的解釋變量。

本文利用具體的個人信貸數據，建立了Group MCP Logistic模型，與Group Lasso和Group Bridge方法進行比較，綜合考慮模型復雜度和預測正確率，發現Group MCP方法是最優的。

因此，基于Group MCP方法建立的Logistic模型，能夠很好地應用在個人信用評價問題研究中。銀行可以結合自己積累的數據，運用Group MCP Logistic模型，選擇出對信用評分影響顯著的變量，對信貸申請人進行信用評分后再決定是否給予貸款，可以很大程度上降低個人信貸風險。

參考文獻：

[1] 方匡南，章貴軍，張惠穎.基于Lasso-logistic模型的個人信用風險預警方法[J].數量經濟技術經濟研究， 2014，（2）：125-136.

[2] 朱曉明，劉治國.信用評分模型綜述[J].統計與決策， 2007，（1）：103-105.

[3] 石慶焱.一個基于神經網絡-logistic回歸的混合兩階段個人信用評分模型研究[J].統計研究，2005，22（5）：45-49.

[4] 胡心瀚，葉五一，繆柏其.上市公司信用風險分析模型中的變量選擇[J].數理統計與管理，2012，31（6）： 1117-1124.

[5] 何曉群，劉文卿.應用回歸分析（第三版）[M].北京：中國人民大學出版社，2011.

[6] 張景肖，劉燕平.函數性廣義線性模型曲線選擇的正則化方法[J].統計研究，2012，29（9）：95-102.

[7] 龐素琳，鞏吉璋.C5.0分類算法及在銀行個人信用評級中的應用[J].系統工程理論與實踐，2009，29（12）： 94-104.

基金項目：國家社科基金項目“個人信用評級的統計建模研究與應用”（項目號：13BTJ004）。

作者簡介：何曉群（1954-），男，漢族，陜西省西安市人，中國人民大學應用統計科學研究中心、中國人民大學統計學院教授、博士生導師，研究方向為統計模型、六西格瑪管理；胡小寧（1986-），男，漢族，河南省濮陽市人，中國人民大學統計學院博士生，研究方向為應用數理統計；馬學俊（1986-），男，漢族，安徽省潁上縣人，中國人民大學統計學院博士生，研究方向為應用數理統計。

收稿日期：2015-06-16。