船用復合材料連接結構穩定性分析方法

于福臨，姚熊亮，郭君，王耀輝

(哈爾濱工程大學船舶工程學院，黑龍江哈爾濱150001)

復合材料具有可設計性強的特點，以其無法比擬的優勢在航空航天、船舶工程、建筑工程、兵器工業等領域得到了應用［1］。夾層復合材料在艦船隱身設計中得到了廣泛應用［2］，采用隱身設計的艦船結構除滿足隱身設計要求外，還需要滿足基本的強度、剛度、穩定性甚至是抗爆性能要求［3］。復合層梁的穩定性計算是結構分析的重要組成部分［4］。船舶桅桿復合材料結構設計中，為保證結構的強度，在結構的端部進行了結構的加強，厚度及材料配置與中間位置不同，使得材料性能存在長度方向上的截面的變化。對于變截面復合材料結構穩定性問題的研究主要集中在復合材料剛度計算方法和失穩臨界載荷的計算［5］，但相關試驗較少。針對船用復合材料連接結構在試驗中出現的失穩模式，采用了傳遞矩陣方法對穩定性計算方法進行分析，并開展了數值仿真和模型試驗，對計算方法的精度進行了驗證。

1 連接結構失穩問題

1.1 模型

圖1表示本文采用的船用復合層梁結構橫剖面形式。表面由彈性模量較大的玻璃鋼組成;芯材由密度低、彈性模量較小的泡沫組成。

船舶桅桿受力復雜，特別是復合層板結構應用到船體上時，在受到重力和風載荷、慣性力等載荷作用時，桅桿與鋼質船體甲板的連接部位容易發生失穩，連接結構的穩定性會影響到桅桿整體性能，應予以重點考核。

圖1 復合材料剖面圖Fig.1 Sandwich composite profile

1.2 穩定性破壞模式

為了研究復合層梁結構的穩定性問題，本文開展了層梁模型穩定性試驗，圖2表示穩定性試驗圖。試驗中，通過MTS系統對試驗樣件施加軸向載荷，至試件產生破壞停止，測量得到軸向失穩載荷。

在試驗中觀察到了不同的失穩模式，圖3和圖4給出了船用復合層梁結構整體和局部失穩試驗圖。

圖2 穩定性試驗布置圖Fig.2 Stability experimental set-up

圖3 復合層梁整體失穩模式圖Fig.3 Mode of composite laminates overall instability

圖4 復合層梁局部失穩模式圖Fig.4 Mode of composite laminates local instability

圖5 力學模型Fig.5 Mechanical model

圖5給出了船用復合材料連接結構穩定性分析力學模型。通過試驗發現了復合層梁結構的穩定性破壞模式，但是沒有適用于船用復合材料連接結構的穩定性計算方法，本文基于試驗中發現的問題，開展了穩定性計算方法研究，提出了基于剛度等效和傳遞矩陣方法的穩定性計算方法。

2 等效剛度計算

2.1 等效彎曲剛度計算

假設在外載作用下，復合材料的各夾層應變相等，各層都為勻質材料。等效彎曲剛度采用下式進行計算［8］:

等效彎曲剛度表示為

式中:i表示夾層，n表示層數，Ei表示第i層材料的彈性模量，Ii表示第i層材料相對于中和軸的慣性矩。

式中:hg1、hg2、hg3為各玻璃鋼夾層厚度，其中hg1=hg2;hf1、hf2為泡沫芯材厚度，其中hf1=hf2。

2.2 等效剪切剛度計算

針對船用復合層梁結構，等效剪切剛度設為，其中為船用復合材料的等效剪切模量［9-10］。

等效剪切剛度可用下式計算:

式中:i表示夾層，n表示層數，hi表示第i層材料的厚度，Gi表示第i層材料的剪切剛度。

船用復合層梁的夾層結構形式導致了橫剖面應力分布不均勻，應用能量法修正復合層梁截面的剪切應力。復合層梁結構如圖1，其中hg1=hg2=hg3=h，hf1=hf2=h*，剪切應變能如下式:

式中:τeq表示等效剪切應力，γeq表示等效剪切應變，Kcor表示修正系數，A表示截面積，Q(x)表示剪力。

則剪切應變能Uγ為

對于矩形截面剪應力有

根據彈性模量的不同，重構剪應力分布［6］，對船用復合層梁結構剪應力進行計算并帶入式(4)可得

其中

由式(13)和式(14)可得剪切修正系數的表達式為

式(9)中，當h=0時或h*=0，Kcor=5/6，說明剪切修正方法是正確的［7］。本文采用的船用復合層梁結構的剪切修正系數為:Kcor=1。

3 基于傳遞矩陣法的復合層梁穩定性計算方法

基于Timoshenko梁理論，應用傳遞矩陣法，對復合層梁結構的穩定性進行求解。對于存在功能梯度的復合層梁的屈曲載荷計算中，采用無長度無質量的轉動彈簧模型對剛度變化進行等效分析［11-12］。

截面上任一點位移:

正應變、剪應變為

軸向力T、彎矩M、剪力Q分別為

一階剪切模型控制方程:

由式(15)可得

將上式代入式(12)～(14)中得

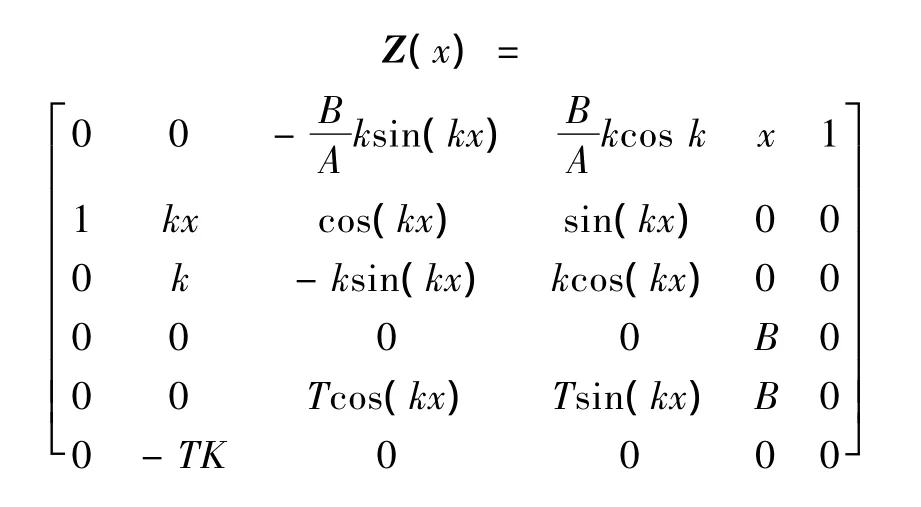
將復合層梁離散成n個分段，對于第i個分段，左端面位置為xi1，右端面為xi2。

可以得到傳遞矩陣:

對于變截面的復合層梁，認為不同離散分段之間位移、軸向力和彎矩連續，而轉角存在間斷［12］。

式中:k*表示剛度系數，φi+1為i+1段的轉角，φi為第i段的轉角。

不同分段相鄰截面之間的變量關系為

式中:

將式(19)代入式(22)可得

可以得到求解復合層梁結構穩定性的傳遞矩陣方程為

對于一端固支，一端自由的復合層梁，根據邊界條件可得特征值計算式為

對于特征值的求解，可以得到一端固支、一端自由的復合層梁的臨界載荷值Pcr。

相對于能量法等理論求解方法，傳遞矩陣方法易于編程，程序化程度高，對于處理功能梯度材料具有更好的通用性，而且計算效率更高。

4 穩定性計算分析

4.1 計算結果與數值計算結果對比

對計算結果進行無量綱化處理，屈曲載荷為crfem，Pcr為FEM和TMM計算得到的屈曲載荷，Pcrfem為FEM得到的屈曲載荷。

TMM表示傳遞矩陣方法，FEM表示有限元方法，從表1與有限元方法的計算結果對比可以看出，傳遞矩陣方法精度較高。

表1 計算結果比較Table 1 Comparison between TMM and FEM values

4.2 理論計算結果與試驗結果對比

對計算結果進行無量綱化處理，屈曲載荷為crtmm，Pcr為試驗和TMM得到的屈曲載荷，Pcrttmm為TMM得到的屈曲載荷。

根據1.2節中試驗，對三組試驗試件進行加載試驗，傳遞矩陣法計算值與試驗值比較見表2。考慮樣件的離散性，對試驗值取平均，將傳遞矩陣法計算結果與試驗值進行對比，平均誤差為10.74%，可以看出傳遞矩陣方法計算精度較高，誤差產生的原因可能是本文提出的方法對撓曲線的描述與實際并不完全一致，并且復合材料試件存在一定的離散性，導致計算結果與試驗產生了一定的誤差。

本文提出的穩定性分析方法可以對整體失穩模式進行計算分析，局部分層失穩是由于面內剪力和層間剪力引起的，對于復合層梁局部失穩還無法進行分析，還需對方法進一步改進。

表2 傳遞矩陣方法計算值與試驗值結果比較Table 2 Comparison between TMM and experimental values

5 結論

本文對船用復合材料與鋼質船體結構連接部位的失穩進行分析，基于傳遞矩陣方法，提出了連接部位復合層梁結構的穩定性理論計算方法。

1)開展了復合材料連接結構失穩破壞模式試驗，發現了整體失穩和局部失穩的失穩模式。

2)根據船用復合層梁的結構形式，對其進行了等效彎曲剛度計算和等效剪切剛度計算，計算并驗證了剪切修正系數。

3)采用傳遞矩陣方法對復合層梁結構的穩定性進行了分析，并與試驗結果進行了對比，計算方法精度較高，對上層建筑與鋼質船體結構連接結構的設計和制造提供了工程設計參考。

［1］劉敬喜，譚安全，李天勻，等.復合材料層合圓柱殼中振動功率流特性［J］.哈爾濱工程大學學報，2012，33(3):269-274.LIU Jingxi，TAN Anquan，LI Tianyun，et al.Characteristics of the vibration power flow in a laminated composite cylindrical shell［J］.Journal of Harbin Engineering University，2012，33(3):269-274.

［2］MOURITZ A P，GELLERT E，BURCHILL P，et al.Review of advanced composite structures for naval ships and submarines［J］.Composite Structure，2011，53:21-41.

［3］HELLER S R.The use of composite materials in naval ships［M］.Oxford:Pergamon Press，1967:69-111.

［4］王穎堅.復合材料層合板的穩定性分析［J］.北京大學學報:自然科學版，1989，1(7):75-89.WANG Yingjian.Stability analysis of composite laminates［J］.Acta Scientiarum Naturalium Universitatis Pekinensis，1989，1(7):75-89.

［5］RAHAI A R，KAZEMI S.Buckling analysis of non-prismatic columns based on modified vibration modes［J］.Communications in Nonlinear Science and Numerical Simulation，2008，13:1721-1735.

［6］ATTARD M M.Global bucking experiment on sandwich columns with soft shear cores［J］.Electronic Journal of Structural Engineering，2011，11(1):21-31.

［7］JENSEN C.Defects in FRP panels and their influence on compressive strength［D］.Lyngby:Technical University of Denmark，2006:90-95.

［8］SURESH S，MORTENSEN A.功能梯度材料基礎制備及熱機械行為［M］.李守新，譯.北京:國防工業出版社，2000:130-150.

［9］Huang H，Kardomateas A G.Buckling and initial post buckling behavior of sandwich beams including transverse shear［J］.AIAA Journal，2002，40(11):2331-2335.

［10］王耀輝.船舶桅桿復合層板結構穩定性計算方法研究［D］.哈爾濱:哈爾濱工程大學，2013:71-72.WANG Yaohui.Research on the calculation method of composite laminate structure stability for ship mast［D］.Harbin:Harbin Engineering University，2013:71-72.

［11］WANG Q，QUSK S T.Repair of cracked column under axially compressive load via piezoelectric patch［J］.Computers＆ Structures，2005，83(15):1355-1363.

［12］魏東，劉應華.含裂紋功能梯度 Euler-Bernoulli梁和Timoshenko梁的屈曲載荷計算與分析［J］.復合材料學報，2010(4):124-130.WEI Dong，LIU Yinghua.Buckling of functionally traded Euler-Bernoulli and Timoshenko beams with edge cracks［J］.Acra Material Composite Sinica，2010(4):124-130.