Banach空間中分數階微分方程解的存在性

胡雨欣, 寇春海, 葛富東

(東華大學 a. 理學院; b. 信息科學與技術學院, 上海 201620)

Banach空間中分數階微分方程解的存在性

胡雨欣a, 寇春海a, 葛富東b

(東華大學 a. 理學院; b. 信息科學與技術學院, 上海 201620)

運用非緊性測度和Darbo不動點定理,研究了Banach空間中的分數階微分方程初值問題解的存在性.

分數階微分方程; 存在性; 非緊性測度; Darbo不動點定理

近30年來，分數階微分方程已經從純數學范疇逐步滲透到眾多學科和工程應用領域，在材料力學、生物學、物理學、控制、多孔介質、電化學、黏彈性理論等方面都有廣泛的應用.人們對分數階微分方程基本理論的研究不再僅限于歐幾里德空間,對于Banach空間中分數階微分方程基本理論的研究也越來越多,主要圍繞解的存在唯一性展開.關于Banach空間中非線性分數階微分方程解的局部存在性問題,已有初步的研究成果,其研究方法一般是將分數階微分方程轉化成等價的Volterra積分方程,在適當的Banach空間中,運用不動點定理證明其存在性[1-8].而Banach空間中分數階微分方程解的全局存在性問題尚未得到實質性的解決[9].

文獻[8]研究了如下形式的分數階微分方程初值問題解的局部存在性問題:

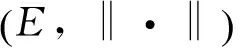
文獻[9]研究了如下分數階微分方程邊值問題解的全局存在性問題：

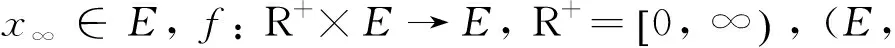
本文主要討論如下分數階微分方程初值問題：

(1)

其中:1<β<2, x0, x1∈E, f:R+×E→E是一個連續映射,(E, ‖·‖)是某個實Banach空間.這里運用非緊性測度和Darbo不動點定理,建立系統(1)在無窮區間上解存在的充分條件.

1　預備知識

定義1.1[10]函數x:R+→R的β階(β>0)Riemann-Liouville分數階積分定義為

其中:x使得上式在R+是逐點有定義的,Γ為Gamma函數.

定義1.2[10]函數x:R+→R的β階(β>0)Caputo分數階微分定義為

其中:n=[β]+1,t>β>0,x使得上式在R+是逐點有定義的.

注1.1對于值域屬于Banach空間的抽象函數x,前面定義中的積分要在Bochner意義下考慮.

引理1.1[10]對β>0,有

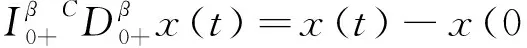
由引理1.1，經過簡單的推算可以得到初值問題(1)等價的積分方程為

(2)

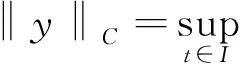
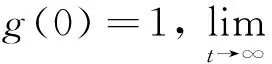
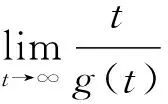
(3)

定義1.3稱f: R+×E→E滿足Caratheodory條件,如果

(1) ?u∈E,t→f(t,u)在R+上強可測；

(2) 對于幾乎所有的t∈R+,u→f(t,u)在E上連續.

下面給出非緊性測度的定義及其部分性質，更多內容請參閱文獻[12-13].

設θ為Banach空間E的零元.記以x為中心,半徑為r的閉球為B(x,r),特別的,記B(θ,r)為Br.

定義1.4非空有界子集D?E的Kuratowski非緊性測度α(D)定義為

α(D)=inf{d>0:

集合D能被有限個直徑小于d的集合所覆蓋}

根據定義易知，對于任意有界子集D,Y?E,Kuratowski非緊性測度α滿足下列性質：

(1) 正則性.α(D)=0當且僅當D是相對緊集，特別的，單元素集的非緊性測度為0.

(2) 單調性.D?Y?α(D)≤α(Y).

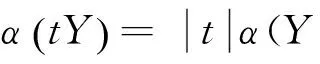
這里分別記α,αC,αX表示空間E,C(I,E),X中有界集的Kuratowski非緊性測度，可以得出以下幾個引理.

引理1.2[13-14]若H?C(I,E)是有界且等度連續的，那么α(H(t))在I上連續且滿足

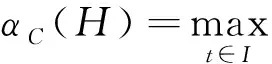
∫Iα(H(t))dt

引理1.3[13](Darbo不動點定理)假設X是一個Banach空間,D?X是一個非空有界閉凸子集,如果算子T:D→D是嚴格收縮的,那么算子T在D中至少存在一個不動點.

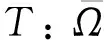
2　主要結果證明

為了采用Darbo不動點定理研究式(1)解的存在性,先將式(1)轉換為等價的算子積分方程.由式(2)易知,式(1)的解在E中的存在性問題可以轉換為下列算子T： E→E的不動點問題

假設映射f滿足下列條件:

(A1) 映射f滿足Caratheodory條件;

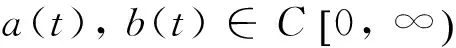
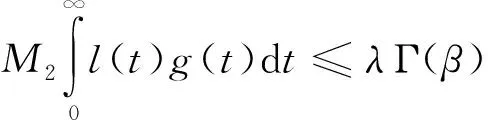
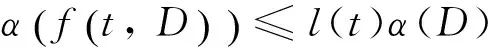
成立，其中0<λ<1.

定理2.1如果分數階初值問題式(1)滿足上述假定條件,那么,在E中至少存在一個解.

為了證明定理2.1,先給出以下幾個引理.

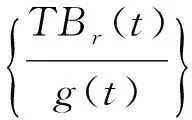
證明根據定義,由條件(A1)可得算子T是連續的.此外,對任意x∈Br?X,即存在常數r>0，滿足‖x‖X≤r.這里有Tx(t)∈E,由條件(A2)可知

‖x0‖+‖x1‖M1+

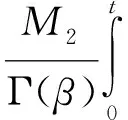
‖x0‖+‖x1‖M1+

‖x0‖+‖x1‖M1+r+

因此,T在Br上是有界的.

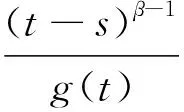
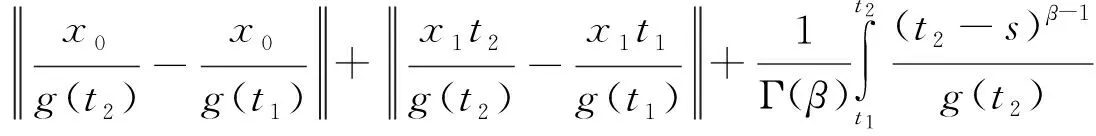
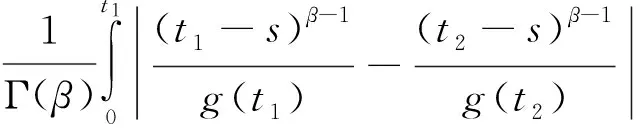
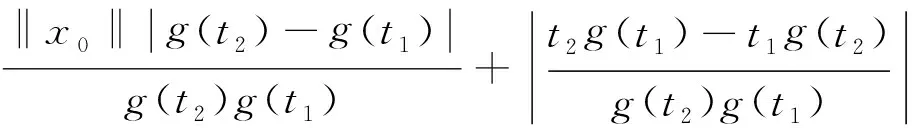
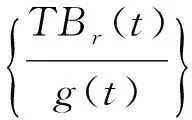
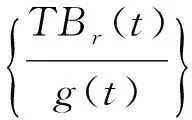
對任意的ε>0,當x∈Br時,由條件(A2)可知,存在常數L1>0,使得

(4)

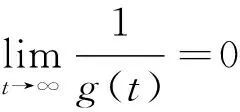
(5)

(6)

(7)

因此,對于任意的t1,t2≥N,根據式(4)～(7)得

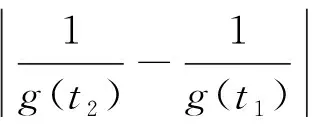
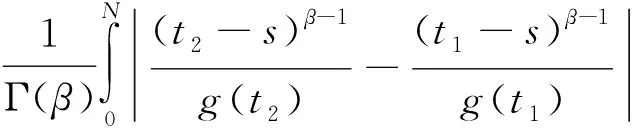
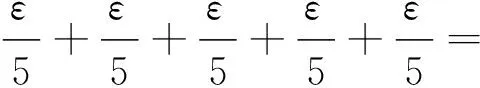
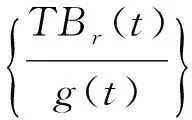
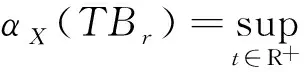
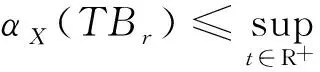
根據引理1.2,?ε>0, ?N>0,當t1,t2≥N時,對任意的x∈Br,都有

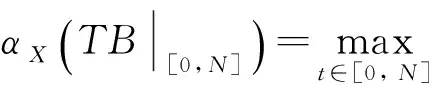
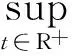
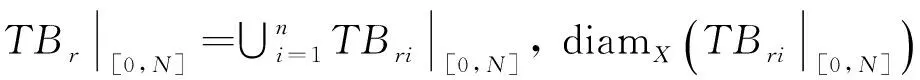
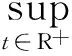
其中:diamX是X的有界子集的直徑.

?Tx1,Tx2∈TBri,t≥N,有

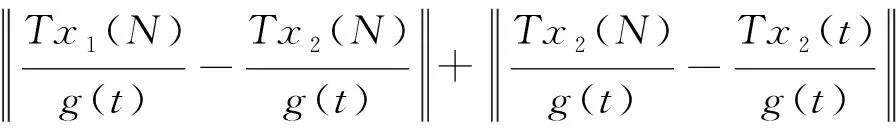
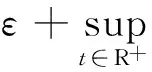
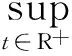
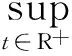
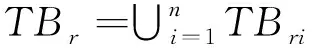
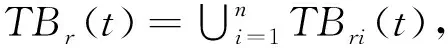
下面給出定理2.1的證明.

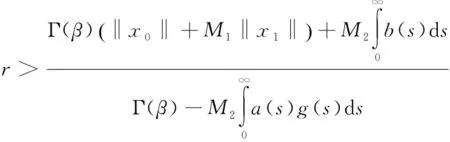
‖x0‖+‖x1‖M1+

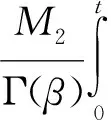
‖x0‖+‖x1‖M1+

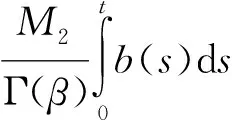
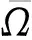
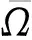
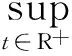
(8)

事實上,當t≤N時,由引理2.1可知，算子T是等度連續的,所以由引理1.2,有

根據引理2.1, ?ε>0, ?N>0,當t1,t2≥N時,對任意的x∈D,都有

因此，當t>N時，

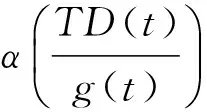
[1] BALACHANDRA K, KIRUTHIKA S, TRUJILLO J J. Existence results for fractional impulsive integrodifferential equations in Banach spaces[J]. Commun Nonlinear Sci Numer Simul, 2011, 16(4):1970-1977.

[2] NGUEREKATA G M. A Cauchy problem for some fractional abstract differential equation with nonlocal conditions[J]. Nonlinear Anal TMA, 2009, 70(5):1873-1876.

[3] SALEM H A H. Multi-term fractional differential equation in reflexive Banach space[J]. Math Comput Modelling, 2009, 49(3/4): 829-834.

[4] ARARA A, BENCHOHRA M, HAMIDI N, et al. Fractional order differential equations on an unbounded domain[J]. Nonlinear Anal TMA, 2010, 72(2): 580-586.

[5] BENCHOHRA M, GRAEF J R, MOSTAFAI F Z. Weak solutions for nonlinear fractional differential equations on reflexive Banach spaces[J]. Electron J Qual Theory Differ Equ, 2010(54): 1-10.

[6] LI K X, PENG J G, GAO J H. Nonlocal fractional semilinear differential equations in separable Banach spaces [J]. Electron J Differ Equ, 2013 (7): 1-7.

[7] LIANG J T, LIU Z H, WANG X H. Solvability for a couple system of nonlinear fractional differential equations in a Banach space[J]. Fract Calc Appl Anal, 2013, 16(1): 51-63.

[8] AGHAJANI A, POURHADI E, TRUJILLO J J. Application of measure of noncompactness to a Cauchy problems for fractional for differential equations in Banach spaces[J].Fract Calc Appl Anal, 2013, 16(4): 962-977.

[9] SU X W. Solutions to boundary value problem of fractional order on unbounded domains in a Banach space[J]. Nonlinear Anal, 2011, 74(8): 2844-2852.

[10] PODLUBNY I. Fractional differential equations [M]. London: Academic Press, 1999.

[11] KOU C H, ZHOU H C, YAN Y. Existence of solutions of initial value problems for nonlinear fractional differential equations on the half-axis[J]. Nonlinear Anal, 2011, 74(17): 5975-5986.

[12] BANAS J, GOEBEL K. Measures of noncompactness in Banach space[R]. Lect Notes Pure Appl Math, 60.New York: Marcel Dekker, 1980.

[13] GUO D J, LAKSHMIKANTHAM V, LIU X Z. Nonlinear integral equations in abstract spaces[M]. Dordrecht: Kluwer Academic Publishers, 1996.

[14] LAKSHMIKANTHAM V, LEELA S. Nonlinear differential equations in abstract space[M]. Oxford: Pergamon Press, 1981.

Existence of Solutions for Fractional Differential Equations in a Banach Space

HUYu-xina,KOUChun-haia,GEFu-dongb

(a. College of Science; b. College of Information Science and Technology, Donghua University, Shanghai 201620, China)

By utilizing the techniques of measures of noncompactness and the Darbo’s fixed point theorem, the existence of solutions of initial value problem for fractional differential equations in a Banach space is investigated.

fractional differential equations; existence; measure of noncompactness; Darbo’s fixed point theorem

1671-0444(2015)06-0867-06

2014-06-05

中央高校基本科研業務費專項基金資助項目(CUSF-DH-D-2014061)

胡雨欣(1989-),女, 山西平遙人, 碩士研究生, 研究方向為分數階微分方程. E-mail：huyuxin2012@126.com

寇春海(聯系人),男,教授,E-mail：kouchunhai@dhu.edu.cn

O 175.6

A