利用微分法計(jì)算定位誤差的改進(jìn)研究

馮酉南 胡文港 葉翰堯

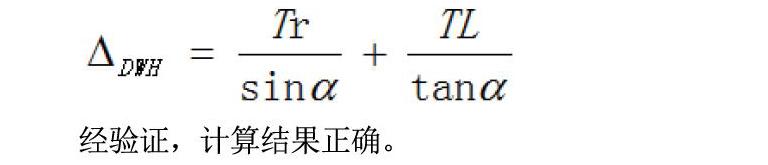
摘 要：定位誤差的計(jì)算是夾具設(shè)計(jì)中不可缺少的重要環(huán)節(jié)。文章將對機(jī)械制造工藝學(xué)中多元素定位誤差微分法求解時(shí)的矛盾進(jìn)行數(shù)學(xué)分析。解釋普通微分法的矛盾原因，并且根據(jù)高等數(shù)學(xué)微分法的性質(zhì)對該算法進(jìn)行改進(jìn)。并通過具體實(shí)例對改進(jìn)方法進(jìn)行驗(yàn)證。

關(guān)鍵詞：定位誤差；微分法調(diào)；整加工法

1 概述

在采用調(diào)整法加工時(shí)，工件的定位誤差實(shí)質(zhì)上就是工序基準(zhǔn)在加工尺寸方向上的最大變動(dòng)量。定位誤差的來源主要有兩方面：1.由于工件定位表面或夾具上的定位元件制作部準(zhǔn)確而引起的定位誤差，成為基準(zhǔn)位置誤差，常用ΔJW表示。2.由于工件的工序基準(zhǔn)與定位基準(zhǔn)不重合而引起的定位誤差，稱為基準(zhǔn)不重合誤差，常用ΔJB表示[1]。定位誤差的計(jì)算時(shí)夾具設(shè)計(jì)中必不可少的重要環(huán)節(jié)，也是檢驗(yàn)夾具是否滿足精度要求的必要條件。目前計(jì)算定位誤差的方法有三種：定義法、合成法、微分法。三種方法從不同的解題思路來計(jì)算定位誤差。所謂定義法是根據(jù)定義，直接求工序基準(zhǔn)的最大變動(dòng)量。合成法是根據(jù)誤差來源，分別計(jì)算出ΔJW和ΔJB，然后求和得出定位誤差定義法和合成法都屬于幾何計(jì)算方法，目前已有的定位誤差自動(dòng)分析軟件大多采用幾何法進(jìn)行計(jì)算。由于尺寸公差遠(yuǎn)小于工件基準(zhǔn)尺寸，因此可以視此微小變量為其公稱尺寸上的微分。微分法就是尋找不受工件尺寸、加工精度影響的固定點(diǎn)，并使該點(diǎn)與工序尺寸有一定的聯(lián)系，這種聯(lián)系必須通過工序尺寸上的投影或者平移而同向（工序尺寸方向同向）建立，從而建立工序基準(zhǔn)點(diǎn)與固定點(diǎn)之間的線性尺寸關(guān)系，通過全微分的方法即可求出該工序定位誤差值[2]

但是普通微分法在多元素定位誤差分析時(shí)可能會得出錯(cuò)誤結(jié)論，本文主要闡述多元素定位誤差微分法計(jì)算時(shí)產(chǎn)生的矛盾，并從高等數(shù)學(xué)的角度進(jìn)行解釋，以此為依據(jù)提出改進(jìn)算法，并用實(shí)例加以證明。

2 問題提出

有一批環(huán)形零件需在內(nèi)孔加工鍵槽，保證尺寸H和t，對稱度誤差不得大于0.03mm。

3 原因分析

定位誤差的微分計(jì)算法是高等數(shù)學(xué)微分近似計(jì)算原理的應(yīng)用。設(shè)函數(shù)Y=F（x1，x2，…xn），當(dāng)自變量x1，x2，…xn分別在x01，x02，…x0n處的變動(dòng)量1XΔ2XΔ…nXΔ都比較小時(shí)，Y的變動(dòng)量可近似的用全微分表示Σ=Δ..=ΔniiiXXYY10[3]

在數(shù)學(xué)中，微分是對函數(shù)的局部變化的一種線性描述。微分可以近似地描述當(dāng)函數(shù)自變量的變化量取值作足夠小時(shí)，函數(shù)的值的變化趨勢。即，微分描述的是函數(shù)的局部變化規(guī)律。以現(xiàn)實(shí)中的現(xiàn)象為例子，移在時(shí)間上的微分就是速度。我們知道，速度是有方向，有大小的。那么從這里我們可以很清楚的看出，微分具有正負(fù)性質(zhì)。再回歸到多元素定位誤差的求解問題中。全微分的每一單一元素iixxLd..都

只反應(yīng)元素xi對L變化的影響，而這個(gè)變化可正可負(fù)。簡言之，當(dāng)xi增加一個(gè)微變量時(shí)，L的變化可能是變大，也可能是變小，這個(gè)是不確定的。定位誤差即是求Lmax-Lmin，由于x1，x2…xn的變化對ΔL的影響可正可負(fù)。[4]比如上邊例子中，當(dāng)φD增加一個(gè)微量尺寸TD時(shí)，AC的長度有所減小，但是當(dāng)φd增加一個(gè)微量尺寸Td時(shí)，AC的長度卻會有所增加。簡單的進(jìn)行全微分的求解而不考慮各個(gè)元素變化的正負(fù)性質(zhì)，這是矛盾存在的根本原因。

4 改進(jìn)方法

普通微分法的局限性在于沒有考慮各個(gè)元素的正負(fù)性質(zhì)。所以必須對微分公式進(jìn)行改進(jìn)。將每個(gè)元素的正負(fù)性質(zhì)考慮的情況下，必須保證累加的每一項(xiàng)都是正值。即，每一單一元素 iixxLT..都要加絕對值符號，才可以保證最后得出正確結(jié)論。

以此方法來驗(yàn)證上述例子，便可得到正確的結(jié)果：

下邊再用另一實(shí)例進(jìn)行證明。

如圖，有一批如圖所示形狀的工件，尺寸φr和L以及夾具角度α均已得到保證，先序在圖示位置加工一通孔，計(jì)算尺寸H的定位誤差。

采用微分法改進(jìn)法進(jìn)行計(jì)算。工序基準(zhǔn)為圓心O，取夾具上頂點(diǎn)A，則AC的表達(dá)式為

用改進(jìn)公式對其進(jìn)行計(jì)算，得到經(jīng)驗(yàn)證，計(jì)算結(jié)果正確。

5 總結(jié)

針對普通微分法求解多元素定位誤差出現(xiàn)的矛盾，本文進(jìn)行了簡要的原因分析，提出了相應(yīng)的改進(jìn)方法。通過典型例子的證明驗(yàn)證了新方法的可行性。

參考文獻(xiàn)

[1]王先逵.機(jī)械制造工藝學(xué)[M].北京：機(jī)械工業(yè)出版社，2013.106—107

[2]馬成習(xí).微分法在定位誤差計(jì)算中的應(yīng)用[J].制造技術(shù)與機(jī)床，2008（4）：130-132

[3]承惠娟，華如.定位誤差的微分計(jì)算法[J].煤礦機(jī)械，2002（1）：37-38

[4]徐鐵華.定位誤差計(jì)算方法探究[J].湖南科技學(xué)院學(xué)報(bào)，2009，30（8）：17-19