例談幾何畫板在小學數學圖形教學中的應用

廖倚春

● 幾何畫板概述

幾何畫板具備平移、反射、旋轉、縮放等變換功能，能實時度量并顯示角度、長度，能在面板中嵌入計算公式展現計算結果，方便學生觀察對比。幾何畫板的操作很簡單，功能很強大，教學實現起來也很方便。能夠順利地幫助學生理解抽象枯燥的數學性質、公式和定理，領會和把握知識之間的內在聯系，從而幫助小學生更好地掌握所學的知識。下面我以三角形為例演示如何運用幾何畫板開展數學圖形教學。

● 教學實例剖析

本實例的主題是繪制相似三角形。但通過該實例，教師還可涉及三角形的繪制、三角形的性質，以及常用的圖形變換——平移、反射、旋轉等。

第一步。在幾何畫板上繪制一個三角形△ABC，并標記三角形各內角角度，各邊長度，如圖1所示。通過拖動三角形的一個端點，演示隨著角度的變化，三角形完成從銳角三角形到直角三角形，再到鈍角三角形的變化。讓學生留意三角形邊長的變化，形象地理解三角形兩邊之和大于第三邊，當兩邊之和等于第三邊時三角形就成了一條直線。并讓學生留意內角和，任意拖動三角形，始終等于180度。

第二步。旋轉三角形，如圖2所示。分別演示該三角形以某點為中心旋轉，如以頂點C為例順時針旋轉30度，得到△AˊBˊC，逆時針旋轉160度，得到△AˊˊBˊˊC。

第三步。利用縮放功能，演示相似三角形，演示圖形如圖3所示。利用不同的縮放比例，可以清晰地向學生演示相似三角形的定理及性質。當然，還可以繪制中線、高線等，證實相關相似比的結論。

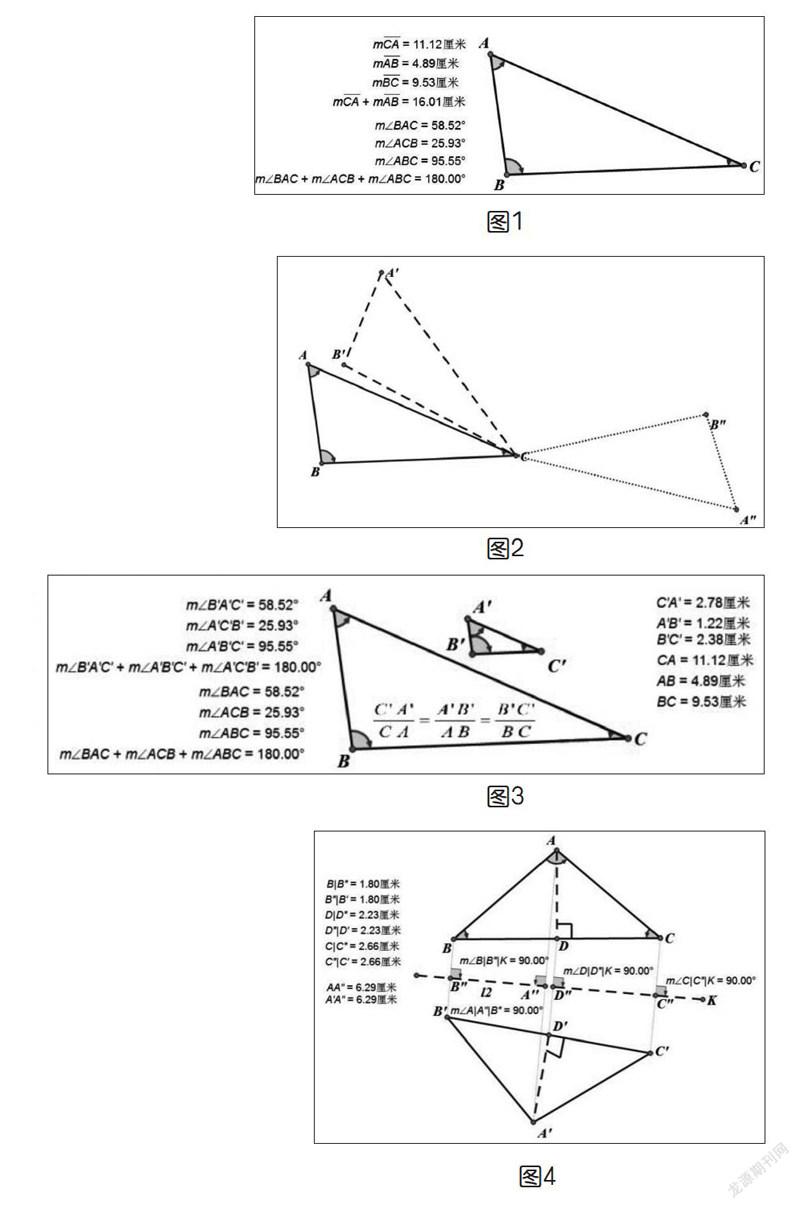
第四步。三角形對稱性演示，翻轉演示，演示圖形如圖4所示。繪制等腰三角形及其高線，測量角度及邊長，為學生演示等腰三角形的幾個性質定理：①等腰三角形的兩個底角相等（簡稱等邊對等角）。②等腰三角形頂角的平分線、底邊上的中線、底邊上的高互相重合（簡稱三線合一），且三角形關于該中線對稱。③有兩個角相等的三角形是等腰三角形。④有一個角等于60度的等腰三角形是等邊三角形。

任意繪制直線l2，利用幾何畫板的反射功能繪制出△ABC關于直線l2對稱的△AˊBˊC。學生由圖形觀察，直觀地認識三角形關于某直線對稱，則有這兩個三角形所有對應點的連線垂直該直線，且對應點到該直線的距離相等。變換、平移△ABC，讓學生觀察上述距離的變化及角度變化。

● 結論

由于文章篇幅所限，幾何畫板在數學教學中的應用實例無法一一列舉，圖形教學是幾何畫板所擅長的，但幾何畫板的功能不僅僅限于圖形教學，在計算、統計及小學高年級學生經常要做的追趕問題、逆向思維訓練等方面都很適用。