逆向思維與數學解題
劉丹丹
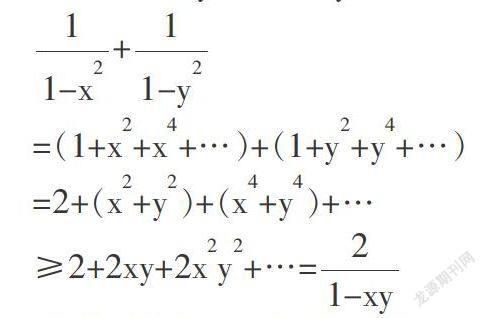

摘 要: 數學解題的過程即思維的過程,而逆向思維是數學思維的一個重要組成部分,也是進行思維訓練的載體.逆向思維通常包括逆轉運算、逆轉結構、逆轉主元、逆轉角度等,在數學解題中合理應用逆向思維,往往能夠突破常規的束縛,產生出奇制勝的效果.
關鍵詞: 逆向思維 數學解題 思維
逆向思維是指與常規正向思維方向相反的思維過程,即通常所說的“倒著想”或“反過來想一想”,是一種創造性的思維方式,體現了思維的靈活性、敏捷性.
1.逆轉運算,提高解題技巧
數學中有眾多定理、公式,并且形式多樣,若能對其作恰當的變形或逆用公式等逆轉運算,則不僅有利于深入領會知識,而且能達到解題靈活、迅速,提高解題技巧的目的.
2.逆轉結構,尋找解題方法
數學解題中,有些題目結構甚為復雜,直接求解很難(解題繁瑣、思路難覓、解題很慢),倘若作逆向思考,可運用關系映射和反演對其結構進行逆轉,從問題結構的調整、簡單化中去打開思路,尋找到解決問題的方法,從而使解題過程化繁為簡,化難為易,變慢為快.
3.逆轉主元,探索解題途徑
數學中部分問題構思巧妙,若按常規思路,思考集中在某些顯然的“主元”上,往往陷入僵局.這時不妨調換“主”與“客”的地位,即變“主元”為“客元”,“客元”為“主元”,往往能取得不錯的效果.
4.逆轉角度,另辟解題捷徑
“橫看成嶺側成峰,遠近高低各不同”,說明從不同角度出發,看到的事物就不同.同理,在數學解題中,也不能局限于單方面考慮問題,多方面、多角度分析才能認清問題的本源,開辟新的解題捷徑.尤其是人們思維的習慣大多是正面的、順向的,而部分題目順向難以認清問題的本質,此時不妨逆轉思考的角度,轉換思維的切入點,也許會柳暗花明,收獲意外的驚喜.
例6:整數1,2,…,n的排列滿足:每個數大于它之前的所有的數或者小于它之前的所有的數.試問有多少個這樣的排列?(1989年加拿大競賽題)
對比上述兩種解法,雖順向思維也可解答該題,但轉變分析的角度后,能更清晰地反映問題的本質,即序列長度每增加1排列個數就變為原來的2倍,也充分挖掘了題目中所滲透的遞歸思想,而這恰恰是順向思維缺失的.多角度分析問題,在解題的同時達到鍛煉思維的目的,不僅有利于今后的數學解題,還能培養計算機編程中所需的思維方法.
波利亞說:“解題的成功靠正確的思路選擇,要靠從可以接近它的方向去攻擊堡壘.”逆向思維與數學解題關系密切,當順向思維面臨困境甚至是絕境時,逆向思維往往出奇制勝,別開生面.正確而巧妙地利用逆向思維,常常使人茅塞頓開,突破思維定勢,探測某些問題的解題方向,找到解題捷徑,使思維進入新的境界.
參考文獻:
[1]張雄,李得虎.數學方法論與解題研究[M].北京:高等教育出版社,2013.
[2]周春荔.數學思維概論[M].北京:北京師范大學出版社,2012.
[3]羅增儒.中學數學競賽的內容與方法[M].南寧:廣西教育出版社,2012.

