數學思想應適時滲透、不斷深入和逐步“領悟”
邱小琴
使學生獲得數學的基本思想是數學課程的重要目標。數學思想是學生數學學習的靈魂,數學思想方法數是數學的靈魂所在,掌握一定的數學思想方法不僅可以使學生更透徹地理解數學知識,對學生的數學學習產生持久的推動力,而且是培養學生創新思想和實踐能力的堅實基礎。數學思想是數學教學的核心和精髓,教師在講授數學方法時應盡力反映和體現數學思想,讓學生了解和體會數學思想,提高學生的數學素養。
一、數學思想的形成需要在過程中實現
只有經歷問題解決的過程,才能體會到數學思想的作用,才能理解數學思想的精髓,才能進行知識的有效遷移。
案例一:五年級的估算教學
……
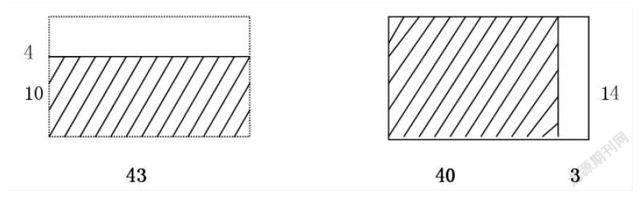
師:估算43×14 你是怎么估的?
生:我把43估為40,40×14=640。
另一位學生又說:我把14估為10,43×10=430。
師:那到底哪個值更接近準確值呢?為什么兩個值會相差這么大呢?
先在小組討論,指名匯報。
過了好一會兒,終于有個學生站起來說:因為43少估了3,也就是3個14,而14少了4,也就是4個43。可大部分學生還是不理解,這時教師出示了兩幅圖:
學生這時恍然大悟,哦,原來是這樣。用圖進行比較真是一目了然。在課的最后進行總結時,教師問:今天你最難忘的是什么?學生回答說,老師用圖來比較40×14和43×10為什么相差這么大,讓我最難忘。
在這節課中,數形結合思想能不失時機地為學生提供恰當的形象材料,把無形的解題思路形象化,更有效地理解算理,不僅有利于學生順利、高效地學好數學知識,更有利于學生學習興趣的培養、智力的開發、能力的增強,使教學收到事半功倍之效。如果教師的教學流于形式,學生的腦中就不會真正建立起“數和形”的聯系。
二、數學思想重在感悟
教學中要讓學生感悟數學思想和方法,關鍵是要讓學生經歷和體驗一些數學知識的獲取過程。
比如,“三角形的分類”的教學,先給學生類別的三角形的卡片,讓學生分小組探討如何對三角形進行分類,給出明確的分類標準,討論同一類的判定、性質,不同三角形的關系。學生在思考和解決這樣問題的過程中,不斷對“如何進行分類”這個問題進行深入思考,并且在與其他同學進行探討的過程中不斷修正和調整自己的想法,逐步找到合理的分類標準。經歷這樣的過程,學生對“分類”思想的認識要比教師直接講結論印象深刻得多。
再如,在一年級“認識圖形”的教學中,教師提供給學生多種不同的物體,有長方體、正方體、球體、圓柱體,如各種包裝盒、積木、茶葉筒等。教師把這些學具放到一起,放手讓學生在學習小組中給這些物體進行分類。學生通過看一看、摸一摸、比一比、想一想、說一說、分一分等方法,從中抽象出四類物體:(1)長方體:有六個平平的面,有的長長的,有的方方的,相對的面都是相等的;(2)正方體:有六個平平的面,是方方的,六個面都是相等的;(3)圓柱體:有2個平平的面,1個彎彎的面;(4)球體:無論怎么看都是圓的,摸來到處是圓溜溜的,可以隨便滾來滾去。在比較、分析中,學生把具有共同特征的物體歸為一類,在分類中抽象出此類圖形的共同特征。在這一探究活動中,學生經歷了分類的過程,滲透了分類的思想、集合的思想、抽象概括的思想等多種數學思想,在掌握知識的同時還形成分類的基本策略,提高學生的數學素養。
三、數學思想的滲透
數學思想的滲透不是簡單地告訴,而應是在教學中組織有效的數學素材,創設認知沖突,適時滲透數學思想,在親歷、交流中讓學生獲得終身發展所需的數學素養。
案例2:五年級的數學廣角“植樹問題”
1.課件出示:同學們在全長1000米的小路一邊植樹,每隔5米栽一棵,一共需要多少棵樹苗?
師:從題目中你得到了什么信息?
師:你覺得種幾棵比較合適?
生匯報:(學生可能會說200棵、201棵等)
2.師:能不能把你的思考過程用簡單的線段圖表示出來呢?如果用圖表示究竟要選擇什么樣的數據來畫呢?有的同學說,我們可以選擇小一點的數據研究,看看棵樹與間隔數存在什么關系,找到規律之后,就可以解決在1000米的路上植樹的問題了。
3.同學們獨立用練習紙上的線段圖畫一畫,我們進行一次模擬植樹活動怎么樣?學生嘗試。
學生匯報,并指明學生到黑板上把圖畫出來。
(1)說說你們是怎樣研究的?你們選擇的數據是多少?有沒有更小一點的數據,也研究出了問題的?
( 2)問什么加1?
4.回顧總結:我們剛才的問題解決經歷了一個怎樣的過程?
師:同學們把復雜的問題轉化為簡單的問題,從較小的數據開始研究,用畫圖的方法幫助我們發現種植棵樹和間隔數的關系,再應用它們的關系說明復雜的問題,這些都是同學們學習方法上的收獲。
在這節課的教學中,教師把數學思想方法以解決學生容易接受的實際問題的形式,通過實驗、觀察、操作、推理等數學活動進行滲透,讓學生在活動中感悟,進一步提高學生的思維能力,激發解決問題的意識,獲得解決問題的策略。教師把數學思想方法由暗線變明線,在學生通過解決問題感受到所蘊含的思想方法,再鼓勵學生運用這一思想方法解決后面的問題。
總之,數學思想離不開具體的數學,空談數學思想是沒有意義的,數學知識與數學思想是緊密聯系的。數學知識的發生、發展過程,也是數學思想的發生和凸顯的過程。只有對數學內容進行深入思考,才能逐步體會其中蘊含的數學思想;只有對相關的數學內容進行聯想、類比,才能感悟數學思想;只有不斷思考問題,才能體會數學思想的作用。

