雙螺桿泵螺桿成型銑刀廓形求解及驗證
王建,董黎敏,劉天航,史津平,郭津津,楊妙妙
(天津理工大學復雜系統控制理論及應用重點實驗室,天津300384)
雙螺桿泵螺桿成型銑刀廓形求解及驗證
王建,董黎敏,劉天航,史津平,郭津津,楊妙妙
(天津理工大學復雜系統控制理論及應用重點實驗室,天津300384)
根據雙螺桿泵螺桿螺旋面端面截形型線方程,利用成形銑削原理和坐標變換理論,從成形銑刀與螺桿工件的相對運動關系出發,建立基本的銑刀刀刃廓形方程。利用Matlab軟件對設計刀具過程中的三角超越方程等非線性方程進行求解,得到銑刀回轉面軸截形,然后以銑刀回轉面軸截形為已知條件,反求螺桿螺旋面端截形,驗證銑刀廓形求解方法的正確性。
成型銑刀;螺桿;廓形;反求
0 前言
雙螺桿泵螺桿成型銑刀屬于復雜刀具,其設計過程異常復雜,其中銑刀廓形的求解是最為關鍵的一步。目前,關于加工螺桿的成形銑刀研究較多,對成形銑刀所加工的螺桿轉子研究較少。本文應用Matlab軟件對求解銑刀廓形以及反求工件端面截形過程中的復雜數學關系式進行求解[1],并給出了計算實例。
1 工件坐標系與刀具坐標系的建立
可轉位成形銑刀加工螺桿時,螺桿與銑刀的相對位置如圖1和圖2所示,在工件上建立坐標系o1-x1y1z1,單位矢量為(i1,j1,k1),在刀具上建立坐標系o2-x2y2z2,單位矢量為(i2,j2,k2)。工件與刀具之間安裝中心的距離為a,安裝角為ψ。
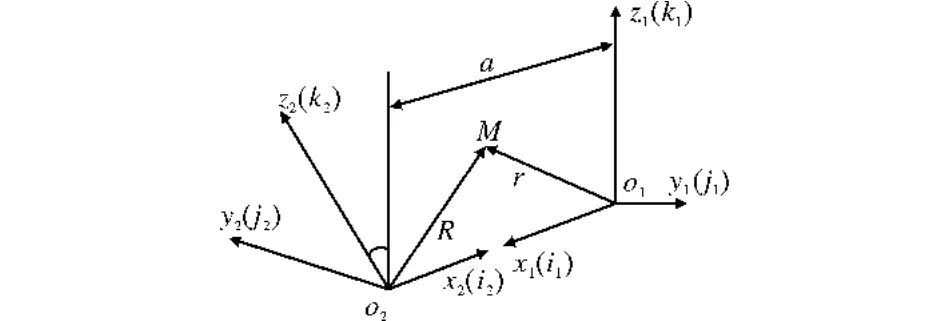
圖1 工件坐標系與刀具坐標系相對位置Fig.1 Relative position of cutter and workpiece coordinate system
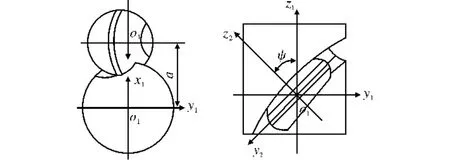
圖2 刀具加工工件螺旋面Fig.2 Helicoid surface of workpiece being cutted
工件坐標系與刀具坐標系的轉換式為
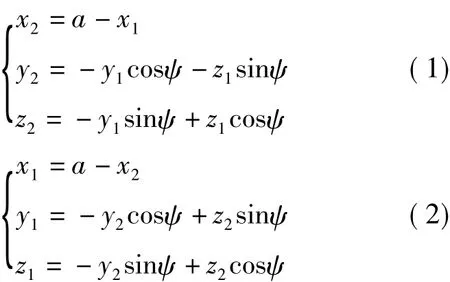
單位矢量間的轉換式為
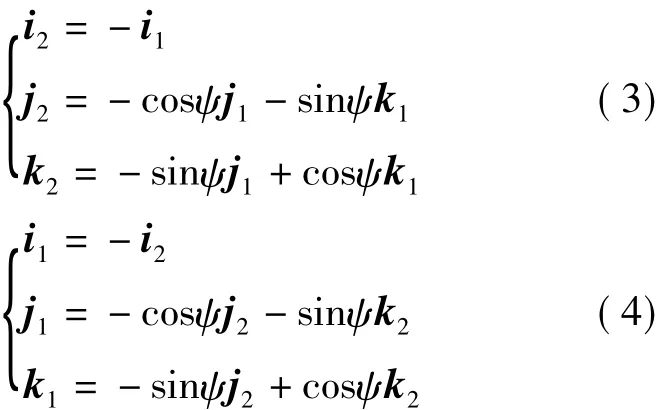
2 刀具回轉面與工件螺旋面的接觸條件式推導
空間中任意一點M相對于工件坐標系原點的徑矢r為
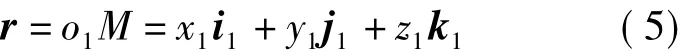
M點相對于刀具坐標系原點的徑矢R為
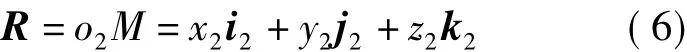
M點相對于刀具坐標系原點的徑矢R與相對于工件坐標系原點的徑矢r之間的關系為
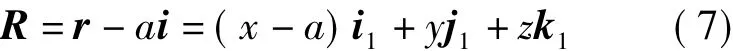
設工件角速度為ω1,螺旋參數為p,刀具的角速度為ω2,M點隨工件螺旋面運動時的線速度v1為
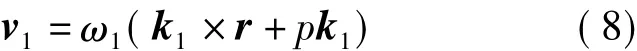
M點隨刀具回轉面運動時的線速度v2為
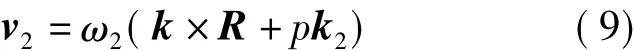
則M點處的相對運動速度v12為
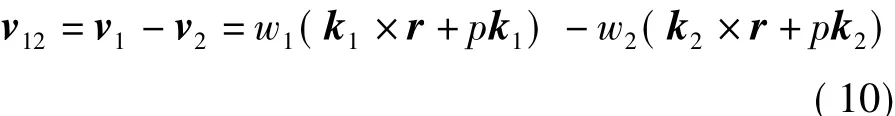
在工件螺旋面和刀具回轉面的接觸點處,其公共法線矢量n與相對運動速度v12垂直,所以接觸條件式為

即刀具回轉面和工件螺旋面的接觸線應滿足的基本條件式
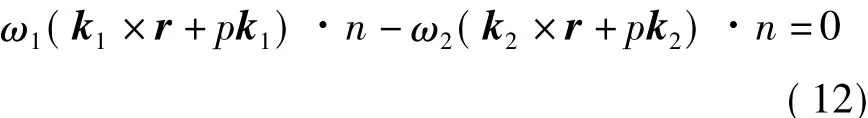
3 已知工件螺旋面端截形求刀具回轉面軸截形
3.1已知工件螺旋面端截形型線方程推導工件螺旋面與刀具回轉面接觸條件式
若工件螺旋面端截形型線方程已知,根據工件螺旋面方程式可求得其上任意一點的法線n,從刀具坐標系的原點o2向螺旋面上的點作徑矢R,如果R和螺旋面上該點的法線n以及刀具的軸線k共面,則這一點就是螺旋面上的接觸點[3],所以工件螺旋面上的接觸線條件式成為
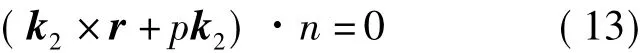
設銑刀所加工的螺桿螺旋面端截形的型線方程式為

式中,t為齒曲線參數。
由式(14)可以得到螺旋曲面的方程為
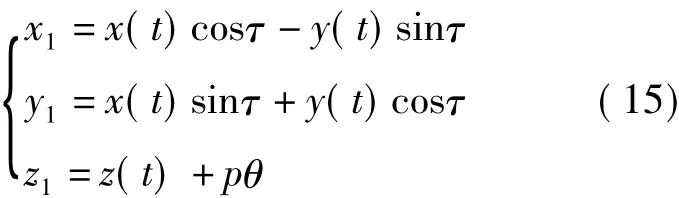
式中,τ為角度參數,表示母線繞z軸轉過的角度。
由微分幾何知識可知,曲面上任意一點M (x,y,z)的法線矢量可以表示為

式中,nx、ny、nz分別是曲面法線矢量的各軸分量。
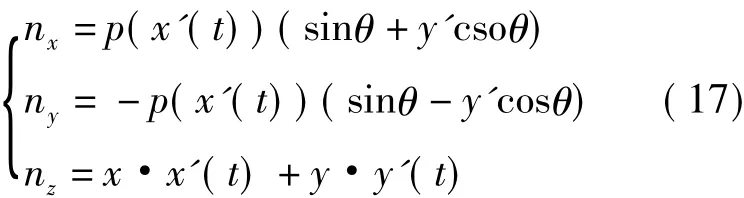
聯立式(4)式(7)式(13)式(17)得到在已知工件螺旋面端截形條件下工件螺旋面與刀具回轉面之間的接觸條件式為

3.2銑刀回轉面軸截形求解計算實例
將齒形參數t離散化為ti得一系列離散點(xi,yi),將(xi,yi)代入螺旋曲面方程求得螺旋面離散點坐標(x1i,y1i),再將(x1i,y1i)與各點處一階導數代入到接觸方程式,選取適當的迭代初值,利用Matlab軟件采用牛頓迭代法對接觸線方程進行迭代運算,求得工件端面上各點成為接觸點時需要轉過的角度τ;然后將坐標值(xi,yi,zi)與此點處的旋轉角τ代入螺旋面方程式,可以得到螺旋面上接觸點的坐標(x1,y1,z1),再將(x1,y1,z1)代入到坐標系變換式,得到接觸點在刀具坐標系內的坐標(x2,y2,z2);最后由刀具回轉面軸截形方程式(21)求得刀具回轉面的軸截形。

銑刀所加工的螺桿轉子參數如下:導程T為150 mm,轉子的齒頂圓直徑為400 mm,分度圓直徑為305 mm。中心距A=(0.7~1.5)D0,此處取A=D0(D0是工件的名義外直徑)。安裝角ψ選擇范圍比較大,一般可按ψ=90°-β選擇安裝角(β是工件外圓螺旋角)。工件螺旋面端截形如圖3所示,所求得的銑刀回轉面軸截形如圖4所示。
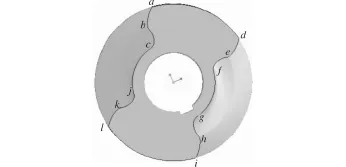
圖3 工件螺旋面端截形Fig.3 Cross section profile ofworkpiece helicoid
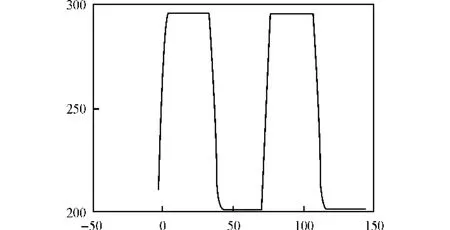
圖4 銑刀回轉面軸截形Fig.4 Axial section of cutter revolution surface
4 由刀具回轉面軸截形反求工件螺旋面端截形
4.1已知刀具回轉面軸截形推導工件螺旋面與刀具回轉面接觸條件式
以求解出的刀具回轉面軸截形為已知條件反求工件螺旋面端截形,根據刀具回轉面的方程式可以求得其上任一點的法線n,由工件坐標系的原點o1向刀具回轉面上的點作徑矢r,如果這一點繞工件軸線作螺旋運動時的線速度矢量和回轉面在該點的法線垂直,則這一點就是回轉面上的接觸點,所以刀具回轉面上的接觸線條件式成為
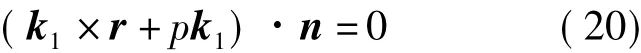
與銑刀固連的坐標系o2-x2y2z2如圖5所示。
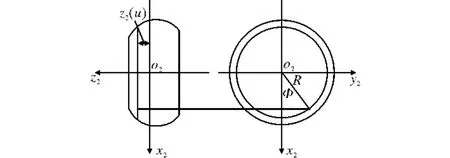
圖5 刀具回轉面坐標系Fig.5 Coordinate system of cutter revolution surface
當截形以未知曲線上的離散點表示時可以用曲線的一般形式來表示[2]

式中,si為弧長,i=1,2,…,n。由弧長微分可得

式中,αi為曲線上點的切線與x軸的夾角。
用盤形刀具加工時,刀具回轉面母線是平面x2y2z2上的一條曲線,按式(21)可以表示為
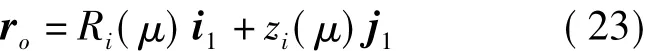
式中,φ為刀具回轉面母線弧長參變數。刀具回轉面方程式可以表示為
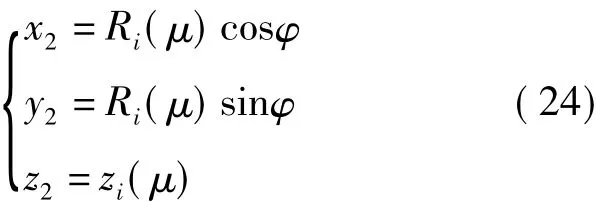
式中,φ為半徑R與o2x2z2平面的夾角。
通過工件坐標系與刀具坐標系的相互轉換,可以得到刀具回轉面在工件坐標系o1-x1y1z1中的方程式為

則刀具回轉面上任意一點各軸的法線矢量為
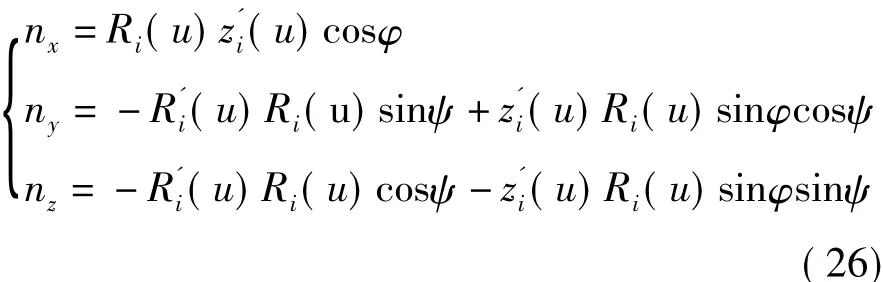
聯立式(3)式(7)式(20)式(26)得到在已知刀具回轉面軸截形條件下刀具回轉面與工件螺旋面之間的接觸條件式:
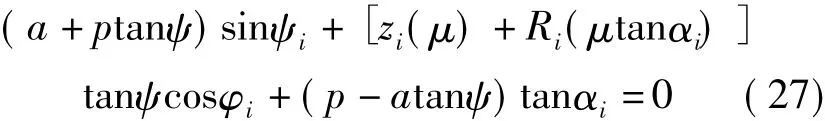
4.2工件螺旋面端截形的求解計算實例
通過接觸線方程可以得知,要想求φ則需先求出α,即銑刀廓形各離散點的傾斜角。本文利用Matlab軟件采用累積三次參數樣條法來計算各離散點處傾斜角α,然后將α代入接觸條件式,采用割線法求出φ。再將銑刀回轉面軸截形離散點坐標及相應的代入工件螺旋面的方程式求出銑刀回轉面軸截形對應的工件螺旋面端截形坐標,最后繪出工件螺旋面端截形,如圖6所示。
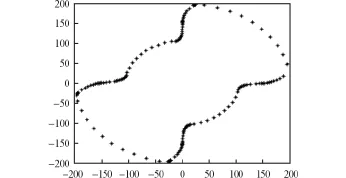
圖6 反求的工件螺旋面端截形Fig.6 Reversing cross section profile of workpiece helicoid
5 結論
本文以右旋螺旋曲面為例,利用齒輪嚙合原理的相關知識,根據已知的螺桿螺旋面端截形型線方程,采用牛頓迭代法求解刀具回轉面與工件螺旋面的接觸線方程,最后求解出刀具回轉面軸截形。以求解出的刀具回轉面軸截形為已知條件,采用累積三次參數樣條法和割線法求解工件螺旋面與刀具回轉面的接觸線方程,最后反求出工件螺旋面端截形,驗證銑刀廓形求解方法的正確性,對可轉位成形銑刀的實際設計具有指導意義。
[1]王小明,羅芝華,楊志,等.基于Matlab的雙螺桿壓縮機轉子盤銑刀數字化設計方法[J].機床與液壓,2012,40(15):84-86,114.
[2]張光輝,魏靜,王黎明.基于離散點截形螺旋面加工原理研究加工原理研究[J].中國機械工程,2007,18(10):1178-1181.
[3]穆存遠,尹木.精密阿基米德絲杠旋風銑削刀具廓型設計[J].機械制造,2004,42(12):41-42.
[4]丁毓峰等.MATLAB從入門到到精通[M].北京:化學工業出版社,2011.
[5]王正林,龔純,何倩.精通MATLAB科學計算[M].北京:電子工業出版社,2009.
[6]李繼峰,鄭青春,郭津津,等.雙螺桿泵雙頭螺旋型線分析及其對流量影響[J].重型機械,2013 (1):55-58.
[7]梅向明,黃敬之.微分幾何[M].北京:機械工業出版社,1981.
[8]吳序堂.齒輪嚙合原理[M].北京:機械工業出版社,1982.
[9]李成松.加工螺旋曲面的盤形銑刀設計系統開發[D].哈爾濱工業大學,2011.
[10]朱建新,李有法.數值計算方法[M].北京:高等教育出版社,2012.
Solution and verification on profile of formed m illing cutter of tw in-screw pump's screw
WANG Jian,DONG Li-min,lIU Tian-hang,SHIJin-ping,GUO Jin-jin,YANG Miao-miao
(Tianjin Key Laboratory for Control Theory&Applications in Complicated Systems,Tianjin University of Technology,Tianjin 300384,China)
According to lines equation of transverse profile of twin-screw pump's screw helicoids,from the relative kinematic relation between formedmilling cutter and screw,the basic profile equation of formedmilling cutter was established bymoldingmilling principles and coordinate transformation theory.Using Matlab software to solve nonlinear equation,such as trigonometric functions in the process of designing the milling cutter,the axial section profile of themilling cutter revolution surface was obtained,and itwas taken as known condition,used for reversing transverse profile of screw helicoids.So the validity of this solution method was verified.
formed milling cutter;screw;profile;converse solving
TG714
A
1001-196X(2015)02-0056-04
2014-06-20;
2014-08-19
天津市科技計劃項目(11ZCKFGX03700)
王建(1988-),男,天津理工大學碩士研究生,研究方向:機械設計及理論等。

