長江經濟帶高技術產業效率測度與異質性分析——基于三階段DEA方法

謝洪軍，張 慧

(重慶理工大學經濟與貿易學院，重慶 400054)

一、引言

后金融危機時代，隨著人口結構的轉變、資源與環境約束趨緊，調整產業結構和轉變經濟發展方式成為我國的迫切任務。2014年12月的中央經濟工作會議明確提出，經濟“新常態”下應堅持以提高質量和效益為中心。這凸顯出當前我國轉變經濟增長，注重發展質量的戰略思想。技術效率能直觀地反映產業效率和核心競爭力，是反映工業經濟增長質量的重要指標之一。作為我國的動力型先導產業，高技術產業在中央及各地區工業經濟中具有舉足輕重的地位。長江經濟帶一直以來被譽為我國的“高科技走廊”，沿江地區高技術產業園區密集，在帶動地區產業轉型升級和地區經濟騰飛中發揮著重要作用。然而，由于區域協調共生和產業聯動機制尚未明確建立，各地區同質性發展和支柱性產業趨同問題日益凸現，其中高技術產業占據著重要地位。在此背景下，對長江經濟帶沿江省市高技術產業的技術效率進行合理評價，比較地區差異和行業差異，以此提出針對性的政策建議，對于探尋提高高技術產業的效率和質量的途徑，優化長江經濟帶沿江高技術產業的資源配置和產業區域發展格局具有長遠的現實意義。

對技術效率的測度，DEA和SFA兩種方法使用最為廣泛。國內外學者也較多采用這兩種方法對高技術產業技術效率進行實證測度。Chung-Jen Chen 和 Chin-Chen Huang[1]、Min-Ren Yan 和 Kuo-Ming Chien[2]利用傳統DEA模型基于臺灣地區高科技工業園區數據分別對高技術產業和企業效率進行了評價。孫劍、李啟明基于此模型對江蘇省13市高技術產業企業的技術效率進行了測度[3]。DEA方法與因子分析方法的結合也已被一些學者所采用[4]。Subal Kumbhakar、Peter Voigt等采用隨機前沿的SFA模型對歐洲高新技術企業2000—2005 年的效率進行了分析[5]。何維達等[6]、范凌鈞等[7]、余泳澤等[8]同樣采用此模型對我國整體及各地區高技術產業的效率進行了測度。鑒于DEA模型和SFA模型本身存在的局限和不足，Fried提出了三階段DEA模型，這一方法對傳統DEA方法進行了改進[9]，因而在近年高技術產業效率研究中被較多采用[10-12]。已有文獻或基于全國層面或某一省份的高技術產業細分行業進行研究，或基于東中西部籠統的區域劃分對高技術產業整體進行研究，但結合長江經濟帶和“高科技走廊”這一新的戰略區域，基于地區和行業細分的視角，對沿江省市高技術產業效率進行合理評價，將更有針對性和參考價值。因此，本文基于沿江11省市2008—2013年數據，借助三階段DEA模型，對長江經濟帶高技術產業效率進行更合理地評價，為沿江地區提高高技術產業各細分行業效率和發展質量，進而為政府決策提供依據和參考。

二、研究方法

DEA模型最早是由Charnes、Coopor和Rhodes于1978提出的。但是傳統DEA測度方法將實際與前沿面的偏離全部歸結為管理無效率因素，不盡合理。因此，Fried提出了三階段DEA方法，剔除非管理因素對效率水平的影響，從而得到反映實際管理水平的效率值[9]。

(一)第一階段:傳統DEA模型

采用投入導向的BCC模型，在規模報酬可變的假定下評估決策單元的有效性。在BCC模型中，綜合效率水平就被分解為純技術效率和規模效率。傳統DEA方法已較為成熟，此處對其線性規劃原理不再贅述。

(二)第二階段:類似SFA回歸

第一階段得出的投入松弛變量受到管理效率、環境因素和隨機因素的影響，第二階段通過構建類似SFA回歸，對第一階段中非有效決策單元的各項投入松弛進行分解，從中分離出環境變量和隨機因素的影響。假設有n個決策單元和m種投入，構建SFA模型:

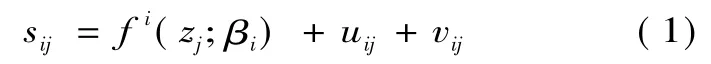
sij表示第j個決策單元的第i項投入的松弛變量，zj=(z1j，z2j，…，zpj)表示 p 個可觀測的環境變量，β為待估計參數。fi(zj，βi)表示環境變量對投入松弛sij的影響，一般取線性形式。uij+vij表示混合誤差，uij表示管理無效率因素，且假定其服從截斷正態分布，即 uij～ N+(μi，)，vij表示產業噪音的隨機誤差因素，假定vij～N(0)，且 vij與 uij相互獨立。定義，當γ越趨向于1，表明管理非有效因素作用越大，模型設定越合理。設γ=0和γ≠0的假設條件下待估計參數的極大似然函數值分別為 L(θ0)和L(θ1)，通過構建LR單邊似然檢驗統計量，來檢驗模型設定的合理性。

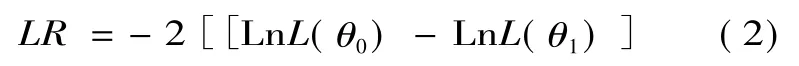
式(2)中，單邊似然檢驗LR符合Mixed χ2分布，當LR大于其臨界值時，拒絕γ=0的原假設，表明模型設定是合理的。根據回歸結果，從中分離出環境變量和隨機因素對投入松弛變量的影響，對決策單元的各項投入進行調整。根據Jondrow提出的方法，得到管理非效率的條件估計量[13]。

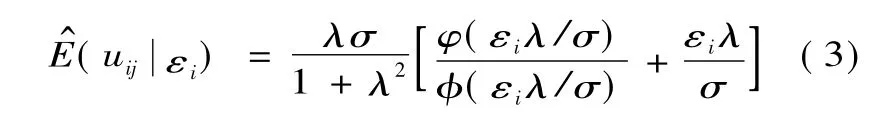
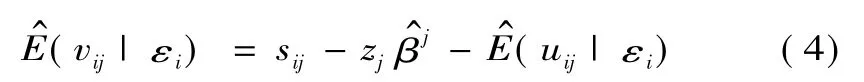
從中分離出環境特征和隨機因素對投入松弛變量的影響，以最有效的決策單元為基準，對所有決策單元的各項投入進行調整

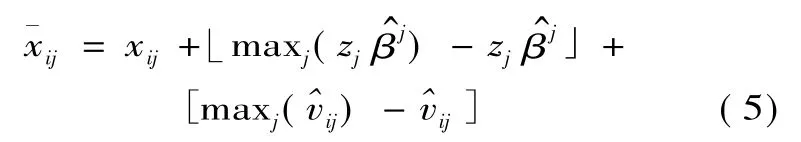
xij和分別表示調整前后的投入量，通過式(5)調整使得所有的決策單元面臨相同的經營環境和運氣。

(三)第三階段:調整后DEA模型

將各決策單元經過第二階段調整后的投入變量和原始產出變量，重新應用BCC模型進行效率測度，從而得到剔除環境變量和隨機因素影響后各決策單元的效率值。

三、實證分析

根據《中國高技術產業統計年鑒》和《中國科技統計年鑒》中對高技術產業的分類標準，基于三階段DEA評價模型，對長江經濟帶沿江11省市高技術產業五大細分行業的技術效率進行測度，包括醫藥制造業、航空航天器制造業、電子及通信設備制造業、電子計算機及辦公設備制造業和醫療設備及儀器儀表制造業。研究的樣本區間為2008—2013年6年的數據。數據來源于2009—2014年的《中國統計年鑒》《中國高技術產業統計年鑒》《中國科技統計年鑒》和《中國科技經費投入統計公報》。

(一)變量定義

1.投入產出變量定義

考慮到高技術產業的屬性和發展特點，選取從業人員年平均人數(X1，人)、R＆D經費內部支出(X2，萬元)和投資額(X3，億元)三項投入指標。利潤是反映產業現期生產運營能力和經濟效益的直接指標，專利申請數排除了人為因素的影響，能夠反映高技術產業的核心競爭力和未來產出增長潛力，因此選取利潤總額(Y1，億元)和專利申請數(Y2，件)兩項作為產出指標。

投入產出指標的選取是應用DEA模型對產業效率進行科學合理評價的關鍵。本文的決策單元為11個，共選取3個投入指標和2個產出指標，滿足模型要求。通過SPSS17.0軟件對投入產出指標的相關性進行檢驗，利潤總額與從業人員年均人數、R＆D經費內部支出、投資額的Pearson相關系數分別為 0.922、0.890、0.964，專利申請數與從業人員年均人數、R＆D經費內部支出、投資額的Pearson 相關系數分別為 0.969、0.942、0.899，且各系數檢驗均通過了1%的顯著性水平，說明指標選取是合理的。

2.環境變量定義

在構建SFA回歸模型中，考慮高技術產業的屬性和發展特點，從宏觀經濟環境、產業競爭程度、科技活動環境和所有制結構4個方面考慮外部不可控因素:選取地區GDP作為宏觀環境因素，選取產業企業數量衡量產業競爭程度，選取科技經費投入強度衡量科技活動環境。由于《中國高技術產業年鑒》從2012年起不再統計總產值和增加值指標，為統一口徑，選取國有企業主營業務收入占行業主營業務總收入的比重作為所有制結構因素。

使用各省市歷年GDP平減指數對地區GDP指標進行平減。由于沒有經費支出、利潤及投資額相關的價格指數，本文以2008年為基期，采用各省市歷年的GDP平減指數對R＆D經費內部支出、投資額、利潤總額三項指標進行平減，得到以2008年為基期不變價格的各項投入產出值。

(二)實證結果

1.第一階段:傳統DEA測度

不考慮環境條件和隨機因素的影響，應用投入導向的傳統DEA中BCC模型，對2008—2013年長江經濟帶沿江11省市高技術產業五大細分行業技術效率進行測度。由于云南省的航空航天器制造業和貴州省電子計算機及辦公設備制造業數據缺失較多，故不做考察。應用Deap2.1軟件對各省市五大行業2008—2013年技術效率測度并求均值，實證結果如表1所示。

表1 調整前各省市分行業5年技術效率均值

在不考慮環境特征和隨機因素影響的情況下，就醫藥制造行業來看，上海和貴州6年均值處于技術效率前沿;云南、江蘇、四川、重慶次之，6年效率均值均達到了0.9以上;江西和湖北技術效率水平均低于0.7，仍有較大的改進空間。對11省市6年效率求均值，醫藥制造行業6年綜合技術效率為0.878，純技術效率和規模效率分別為0.940、0.932，整體效率情況良好。

航空航天器制造業，安徽省處于技術效率前沿，純技術效率和規模效率都達到最優。其次為重慶、浙江、江蘇，效率均達到0.8以上。上海、湖南、湖北四省市技術效率均在0.6以下，其中湖北省最低，效率整體情況不理想。進一步分析發現，四省市低效率水平主要源自純技術效率水平較低。

電子及通信設備制造業，貴州技術效率最高，處于效率前沿面。云南和浙江效率水平也相對較高，為0.9以上。其次為安徽、上海、江西。湖南在11省市中效率值最低，僅為0.694，其純技術效率低于規模效率，成為綜合效率的制約因素。

電子計算機及辦公設備制造業，浙江處于效率前沿。四川、云南次之，均達到了0.95以上，兩省市純技術效率均達到了最優。湖南和江蘇技術效率整體情況也相對較好。湖北和重慶相對效率水平最低，前者主要純技術效率較低有待提高，后者是由于純技術效率和規模效率均不高所致。

醫療設備及儀器儀表制造業，上海、浙江、湖南三省市處于效率前沿。四川和安徽次之，效率均達到0.95及以上。江西技術效率為0.541，遠低于其他10省市。進一步發現其低效率水平源自純技術效率較低，仍有較大的提升空間。

在不考慮環境條件和隨機因素的條件下，長江經濟帶高技術產業中，醫藥制造業、電子及通信設備制造業和醫療設備及儀器儀表制造業綜合技術效率分別為 0.878、0.832、0.869，純技術效率和規模效率均遠高于其他兩行業。

2.第二階段:類似SFA回歸

為剔除環境變量和隨機因素對技術效率的影響，第二階段針對第一階段中非有效決策單元，以各項投入變量冗余為被解釋變量，以上文中構建的4個環境變量為解釋變量進行回歸分析。應用Frontier4.1軟件，回歸結果如表2所示。

3個投入松弛變量的回歸模型中，大部分環境變量的參數都至少通過了10%顯著性檢驗，γ均達到了0.999，表明管理無效率因素對各投入松弛變量產生了重要影響。且三個模型中LR單邊檢驗均通過1%的顯著性水平，表明構建類似SFA回歸模型是合理且必要的。

3.第三階段:調整后DEA測度結果

利用式(5)對所有決策單元的各項投入變量進行調整，對調整后的投入變量和原始產出變量重新應用投入導向的BCC模型進行效率測度，實證結果如表3所示。

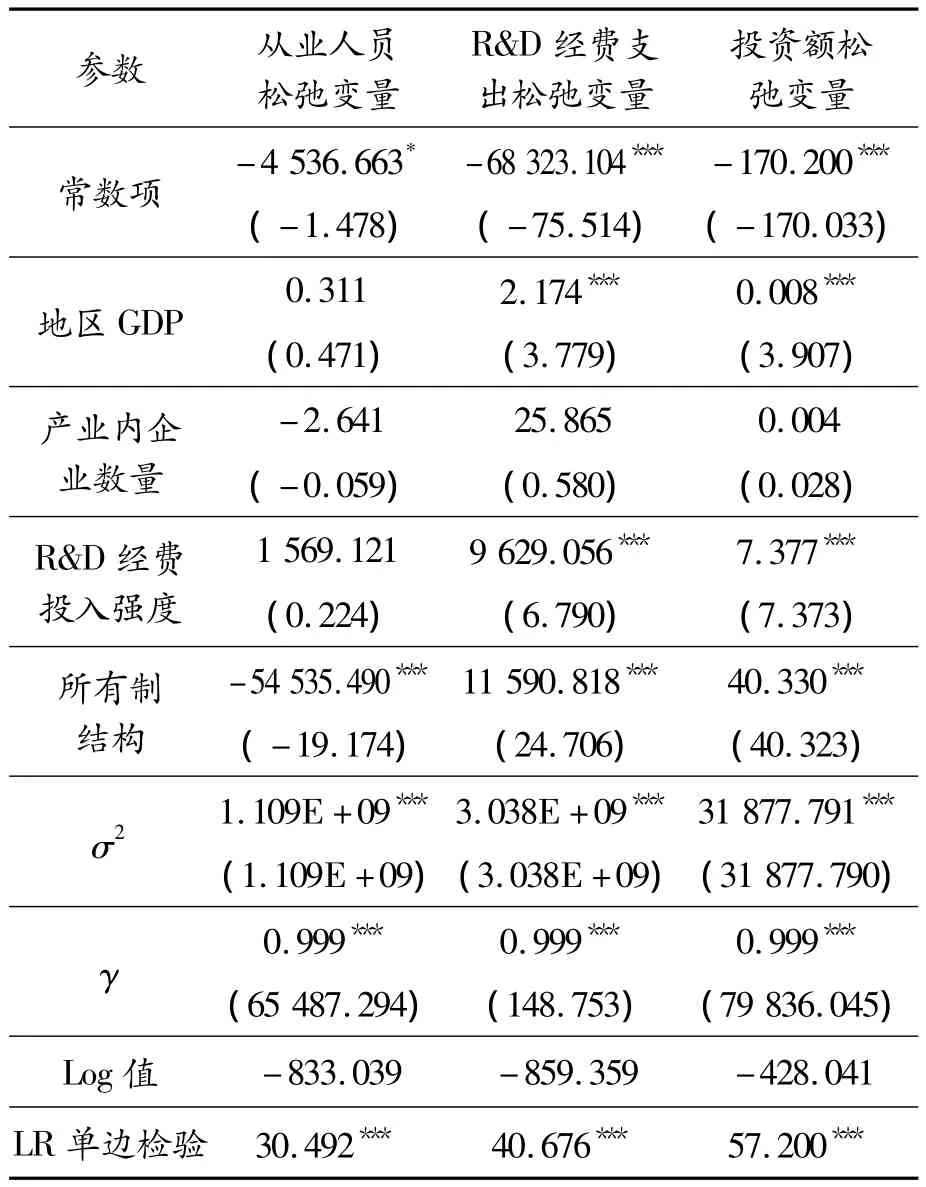
表2 類似SFA回歸結果

表3 調整后各省市分行業五年技術效率均值

對比表1和表3剔除環境變量和隨機因素的影響前后，各省市五大行業6年技術效率均值有明顯改變，說明環境變量和隨機因素會使技術效率評估出現偏差。調整后，醫藥制造業，上海和四川處于效率前沿;航空航天器制造業，江蘇省處于效率前沿;電子及通信設備制造業，上海和浙江效率明顯提高，與貴州一并處于前沿，江蘇和四川效率水平也顯著提高，云南、湖南和重慶明顯降低;電子計算機及辦公設備制造業，調整后浙江仍處于技術效率前沿，除了江蘇效率提高外，大部分地區效率水平出現大幅下降，主要是調整后規模效率大幅下降所致;醫療設備及儀器儀表制造業，上海和浙江仍處于效率前沿，效率水平大多出現下降。

剔除環境和隨機因素影響后，同質環境下11省市6年效率均值除醫藥制造和電子通信設備制造業綜合技術效率水平有所提高外，其他行業效率均值均出現下降，進一步分析發現航空航天器制造業則源自規模效率水平的下降，其他兩行業是由純技術效率和規模效率共同下降所致。調整后效率的行業差異依然存在，醫藥制造業和電子及通信設備制造業效率水平較高，其他3個行業技術效率不盡理想。

四、結論與建議

本文應用三階段DEA評價模型，對長江經濟帶沿江11省市高技術產業五大細分行業的技術效率進行實證測度，得出主要結論如下:

第一，沿江省市效率水平受到環境特征和隨機因素的影響，剔除這些影響因素后，高技術產業各行業效率水平并不理想，仍有很大提升空間。調整后，除電子及通信設備制造業外，其他行業的綜合技術效率均出現下降，技術效率水平較低。地區GDP、R＆D經費投入強度、國有企業占行業比重對R＆D經費支出和投資額兩項投入冗余具有顯著的正向作用，造成了資源的浪費，影響了產業效率水平。

第二，效率水平存在明顯的行業差異和地區差異。從行業來看，醫藥制造業、醫療設備及儀器儀表制造業和電子及通信設備制造業3個行業的效率遠高于其他兩個行業，且剔除環境特征和隨機因素影響后，差異仍存在。就地區來看，各地區5個行業的效率水平和優勢產業也存在差異。

長江經濟帶一直以來被譽為我國的“高科技走廊”。然而實證結果表明，現有條件下，沿江高技術產業的實際產出并未達到最大化，效率水平并不理想，且存在較大的行業差異和地區差異。沿江省市應充分發揮特色資源和比較優勢，有針對性地提高經營管理水平或規模收益，提高高技術產業的效率水平和發展質量。在“一帶一路”國家戰略實施的背景下，以高技術產業為支點，充分發揮高技術產業對其他產業的輻射和帶動作用，促進人員、技術、資本等要素在長江經濟帶產業間的合理高效流動，有利于優化資源配置的區域結構和產業結構，形成優勢互補、錯位發展的競爭格局，避免下一輪粗放型增長和地區競爭中出現的低水平重復建設和產能過剩。

[1]CHEN C J，HUANG C C.A multiple criteria evaluation of High Tech industries for the science-based industrial park in Taiwan[J].Information ＆ Management，2004(7):839-851.

[2]YAN M R，CHIEN K M.Evaluating the Economic Performance of High-Technology Industry and Energy Efficiency:A Case Study of Science Parks in Taiwan[J].Energies，2013(2):973-987.

[3]孫劍，李啟明.高新技術企業投入產出效率評價——基于江蘇十三個城市的實證研究[J].科學學研究，2008(10):62-64.

[4]容美平，王斌會.我國各地區高技術產業投入產出效率綜合評價[J].科技進步與對策，2010(7):26-28.

[5]KUMBHAKAR S C，LOVELL C.Stochastic Frontier Analysis[M].New York:Cambridge University Press，2000.

[6]何維達，張遠德.基于非參數隨機前沿面模型的高技術產業效率研究[J].經濟經緯，2008(4):71-74.

[7]范凌鈞，李南，陳燕兒.中國高技術產業技術效率區域差異的實證分析[J].系統工程，2011(2):57-62.

[8]余泳澤，張妍.我國高技術產業地區效率差異與全要素生產率增長率分解——基于三投入隨機前沿生產函數分析[J].產業經濟研究，2012(1):45-51.

[9]FRIED，LOVELL C，et al.Accounting for Environmental Effects and Statistical Noise in Data Envelopment Analysis[J].Journal of Productivity Analysis，2002(17):121-136.

[10]王軍，楊惠馨.2006—2008年中國省際高技術產業效率實證研究[J].統計研究，2010(12):47-49.

[11]吉生保，周小柯.基于三階段DEA模型的中國高技術產業效率研究[J].中央財經大學學報，2010(12):62-66.

[12]張穎.基于三階段DEA模型的安徽省高技術產業效率分析[D].合肥:安徽大學，2013.

[13]JONDROW J，LOVELL C A K，MATEROV I S.On The Estimination of Technical Inefficiency in the Stochastic Frontier Production Function Model[J].Journal of Econometrics，1982(19):233-238.