石墨烯納米結(jié)構(gòu)中負(fù)微分電阻效應(yīng)研究

徐公杰　李娜　陳鏡

摘要： 由于石墨烯具有高電子遷移率的特性，可以用來(lái)制備高頻電子器件。利用傳輸矩陣方法，對(duì)石墨烯p-n結(jié)及方形勢(shì)壘納米結(jié)構(gòu)中的負(fù)微分電阻效應(yīng)進(jìn)行了研究。證實(shí)了石墨烯p-n結(jié)中負(fù)微分電阻現(xiàn)象比傳統(tǒng)半導(dǎo)體中的幅度要小，石墨烯中Klein隧穿過(guò)程的存在使負(fù)能量范圍內(nèi)的空穴對(duì)電流產(chǎn)生影響。石墨烯納米方形勢(shì)壘中發(fā)生負(fù)微分電阻效應(yīng)的位置在費(fèi)米面附近，勢(shì)壘寬度越大，對(duì)載流子的阻擋越大，負(fù)微分電阻效應(yīng)越明顯。

關(guān)鍵詞： 石墨烯； 負(fù)微分電阻； 傳輸矩陣

中圖分類(lèi)號(hào)： TN 361文獻(xiàn)標(biāo)志碼： A doi： 10.3969/j.issn.1005-5630.2015.04.011

Abstract： The negative differential resistance （NDR） effect of graphene in the p-n junctions and nanoscale barriers is investigated by using transfer-matrix method. The NDR phenomenon in the graphene p-n junctions is not so obvious as that in the conventional semiconductors， because the holes in the negative energy range also contribute to the current due to the Klein tunneling. The NDR location of graphene nanoscale barriers lies on the Fermi energy level. The block of the barrier to the current is more apparent with increasing barrier width， and the NDR effect becomes more obvious.

Keywords： graphene； negative differential resistance （NDR）； transfer matrix

引 言

石墨烯（graphene）[1-2]是由單層碳原子按六角晶格結(jié)構(gòu)排列而成，它是一種真正意義的二維體系。由于石墨烯在電學(xué)、力學(xué)、光學(xué)、熱學(xué)等各方面都具有優(yōu)異的物理性質(zhì)[3-4]，所以自2004年英國(guó)曼徹斯特大學(xué)的Novoselov與Geim成功制取以來(lái)，特別是這2位獲得2010年諾貝爾物理學(xué)獎(jiǎng)以后，石墨烯更是引起物理、材料、化學(xué)等各領(lǐng)域的極大關(guān)注，并使之迅速成為基礎(chǔ)理論與應(yīng)用的研究熱點(diǎn)之一。

負(fù)微分電阻（negative differential resistance，NDR）效應(yīng)[5]一般是指在n型的GaAs 和 InP等雙能谷半導(dǎo)體中，由于電子轉(zhuǎn)移效應(yīng)（transferred-electron effect）而產(chǎn)生的一種效應(yīng)，即隨著電壓增大而電流呈現(xiàn)減小的現(xiàn)象。在負(fù)阻區(qū)，半導(dǎo)體中載流子濃度局部的微小漲落即可引起非平衡多數(shù)載流子的大量積累而產(chǎn)生空間電荷，這種現(xiàn)象就是負(fù)微分電阻效應(yīng)。它是耿氏（Gunn）二極管工作的物理基礎(chǔ)，是現(xiàn)階段制備高頻電子器件的重要技術(shù)途徑。本文利用傳輸矩陣的方法，針對(duì)典型的p-n結(jié)和方形勢(shì)壘結(jié)構(gòu)分別研究其中的負(fù)微分電阻效應(yīng)，并討論影響因素及物理原因。

1 原理與公式

1.1 原理

石墨烯的每一個(gè)碳原子最外層4個(gè)電子與周?chē)?個(gè)最近鄰原子進(jìn)行sp2雜化，形成3個(gè)σ鍵，剩余1個(gè)電子在pz軌道上與周?chē)娮有纬搔墟I。石墨烯每個(gè)原胞中含有2個(gè)不等價(jià)的原子，對(duì)應(yīng)于布里淵區(qū)的K與K′點(diǎn)（k空間中高對(duì)稱點(diǎn)），又叫Dirac點(diǎn)。Dirac點(diǎn)附近（小于1eV范圍）的電子遵循著無(wú)質(zhì)量費(fèi)米子的Dirac方程，它有線性的色散關(guān)系E（k）=±vFk[4]，其中E代表載流子能量，vF代表費(fèi)米速度106 m·s-1，k代表波矢，代表簡(jiǎn)約普朗克常數(shù)。而且導(dǎo)帶底與價(jià)帶頂是直接相連，屬于一種無(wú)帶隙的材料體系。石墨烯的色散關(guān)系與傳統(tǒng)出現(xiàn)負(fù)微分電阻效應(yīng)的材料如GaAs或InP的雙能谷完全不同，但研究發(fā)現(xiàn)其中有負(fù)微分電阻效應(yīng)[6-7]。由于石墨烯中電子遷移率高達(dá)106 cm2·（V·s）-1[8]，而GaAs的這一數(shù)值為8 000 cm2·（V·s）-1，Si中為1 450 cm2·（V·s）-1 [5]。人們利用石墨烯高電子遷移率這一特性，制備高頻電子器件，如毫米波及太赫茲（1 THz=1012 Hz）波器件，而負(fù)微分電阻效應(yīng)是這些器件的物理基礎(chǔ)。

1.2 傳輸矩陣方法

在石墨烯中，電摻雜[9]或化學(xué)摻雜[10]均可使其表現(xiàn)出p型或n型特性，而這種摻雜本身會(huì)形成一個(gè)勢(shì)場(chǎng)。在此討論一維勢(shì)場(chǎng)U（x）情形，且假設(shè)處于零溫近似下，暫時(shí)不考慮載流子聲子相互作用、自旋軌道相互作用，且假設(shè)樣品足夠?qū)捒梢院雎赃吔缧?yīng)。此時(shí)Dirac方程可寫(xiě)成[6，11-12]

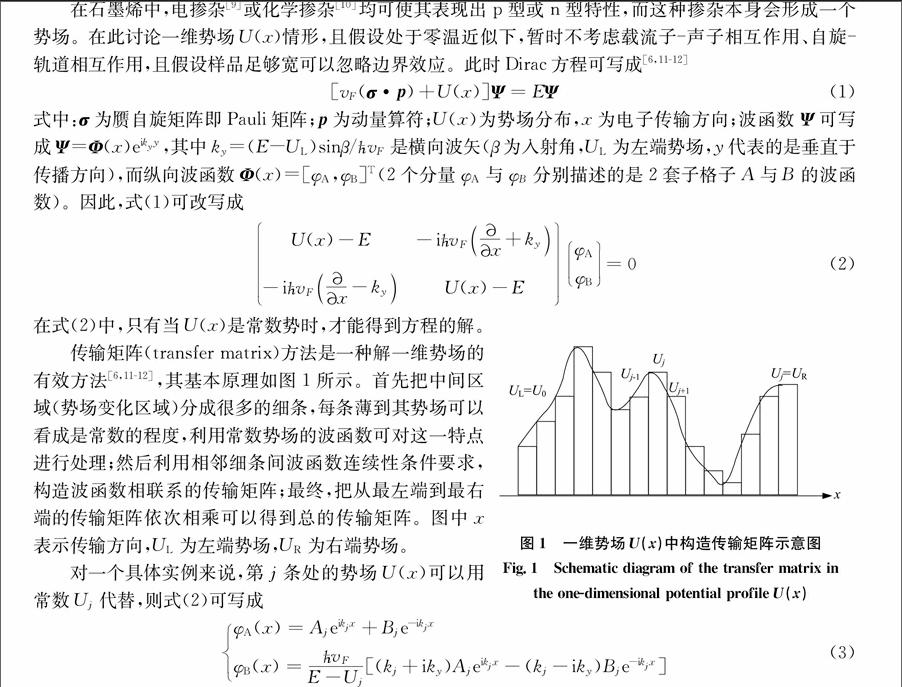
傳輸矩陣（transfer matrix）方法是一種解一維勢(shì)場(chǎng)的有效方法[6，11-12]，其基本原理如圖1所示。首先把中間區(qū)域（勢(shì)場(chǎng)變化區(qū)域）分成很多的細(xì)條，每條薄到其勢(shì)場(chǎng)可以看成是常數(shù)的程度，利用常數(shù)勢(shì)場(chǎng)的波函數(shù)可對(duì)這一特點(diǎn)進(jìn)行處理；然后利用相鄰細(xì)條間波函數(shù)連續(xù)性條件要求，構(gòu)造波函數(shù)相聯(lián)系的傳輸矩陣；最終，把從最左端到最右端的傳輸矩陣依次相乘可以得到總的傳輸矩陣。圖中x表示傳輸方向，UL為左端勢(shì)場(chǎng)，UR為右端勢(shì)場(chǎng)。

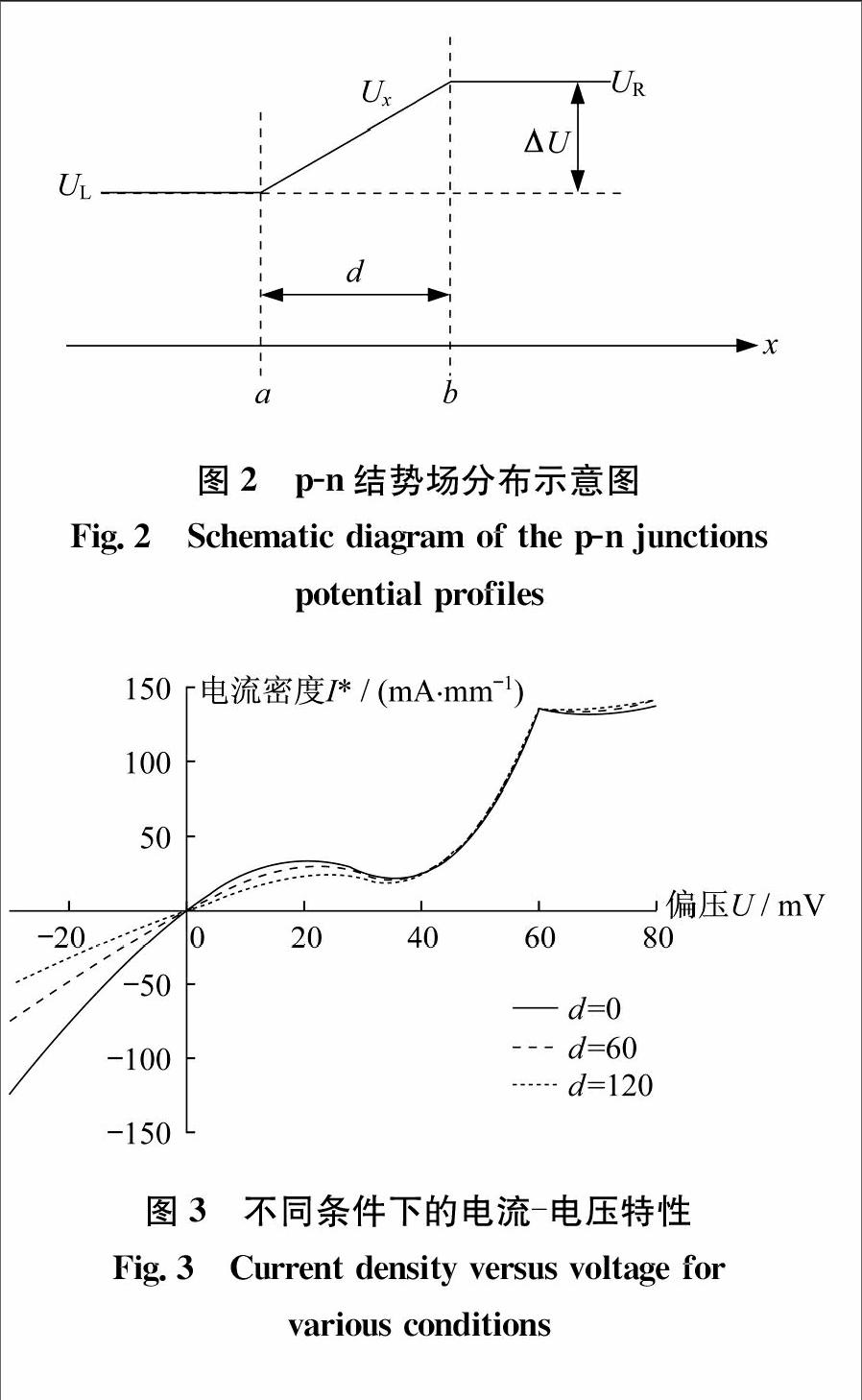
圖3中的電流電壓曲線與所謂的Esaki二極管[5]類(lèi)似，所不同的是正偏壓下的負(fù)微分電阻幅度變小了。這種負(fù)微分電阻的減小與石墨烯的手征性有關(guān)，因?yàn)殡娮优c空穴（負(fù)能量范圍內(nèi)）對(duì)電流都有貢獻(xiàn)，所以負(fù)能量范圍內(nèi)的電流貢獻(xiàn)是負(fù)微分電阻減小的主要原因。Dragoman等[13]曾經(jīng)計(jì)算過(guò)方形勢(shì)壘中的透射率，因?yàn)闆](méi)有計(jì)入負(fù)能量范圍內(nèi)載流子的貢獻(xiàn)，得到明顯的負(fù)微分電阻，引起了爭(zhēng)論[14]。因此，這種電子空穴對(duì)稱性引起的負(fù)微分電阻減弱可能是石墨烯納米結(jié)構(gòu)中的一種普適特性。圖3中在U=60 mV處出現(xiàn)的突變點(diǎn)源于此時(shí)U=ΔU，此時(shí)外加偏壓將原勢(shì)階抹平，并且當(dāng)U>ΔU時(shí)，原來(lái)的p型（n型）變成了n型（p型）。正偏壓使原勢(shì)階減小這一結(jié)果使Klein隧穿，當(dāng)載流子垂直于勢(shì)壘或勢(shì)阱入射時(shí)，不管勢(shì)壘或勢(shì)阱高度及寬度如何變化，透射率始終為1。產(chǎn)生的物理原因是在勢(shì)阱中載流子是電子，在勢(shì)壘中對(duì)應(yīng)的載流子變成了空穴 [15]，能量區(qū)域也減小，因此d對(duì)伏安特性影響不大；而當(dāng)偏壓加大了原勢(shì)階，Klein隧穿區(qū)域隨|U|的增加而加大，這就產(chǎn)生了電流幅度隨d的增加出現(xiàn)明顯的減小。

2.2 方形勢(shì)壘中的負(fù)微分電阻

當(dāng)勢(shì)階變成方形勢(shì)壘后，為驗(yàn)證這種負(fù)微分電阻效應(yīng)是否還會(huì)出現(xiàn)，本文采取如圖4所示的模型，這與文獻(xiàn)[12]模型相同。假設(shè)壓降發(fā)生在勢(shì)壘邊緣區(qū)，勢(shì)壘高度為U0，寬度為D，實(shí)線和虛線分別表示有無(wú)偏壓后的勢(shì)場(chǎng)分布，同時(shí)假設(shè)外加偏壓對(duì)稱降落在勢(shì)壘邊緣。由于外加偏壓的引入使原來(lái)勢(shì)場(chǎng)變得不再對(duì)稱，與本文采用的計(jì)算方法不同，文獻(xiàn)[12]只針對(duì)某一入射角計(jì)算電流，并且結(jié)果中忽略了負(fù)能量范圍內(nèi)載流子對(duì)電流的貢獻(xiàn)，而本文采用的是傳輸矩陣方法，對(duì)所有入射角度積分，并且計(jì)入所有載流子貢獻(xiàn)。

圖（5）給出了影響負(fù)微分電阻效應(yīng)的因素費(fèi)米能級(jí)位置與勢(shì)壘區(qū)域?qū)挾取１娝苤瑢?duì)電流有貢獻(xiàn)的載流子處于費(fèi)米面附近，所以當(dāng)費(fèi)米能增大時(shí)，發(fā)生負(fù)微分電阻現(xiàn)象的電壓位置也隨之增大平移，如圖5（a）所示。這種平移的原因是式（13）中|E-UL|項(xiàng)，此處UL=eUa/2，而E的取值區(qū)間是[EF-eUa/2，EF+eUa/2]，所以當(dāng)eUaEF時(shí)，出現(xiàn)電流較小值，對(duì)應(yīng)于負(fù)微分電阻出現(xiàn)的電壓位置。因此，當(dāng)勢(shì)壘寬度一定時(shí)，隨著費(fèi)米能的增加，電流-電壓曲線中負(fù)微分電阻出現(xiàn)的位置也相應(yīng)增大。圖5（b）中給出了當(dāng)費(fèi)米能一定

時(shí)，勢(shì)壘寬度對(duì)負(fù)微分電阻的影響。相同條件下，隨著勢(shì)壘寬度的增加，透射率會(huì)呈現(xiàn)一定程度的減小[16]，因此對(duì)電流的貢獻(xiàn)也就減少，因而，圖5（b）中勢(shì)壘寬度最小的結(jié)構(gòu)電流最大，相應(yīng)的負(fù)微分電阻現(xiàn)象最不明顯。隨著寬度的增加，勢(shì)壘對(duì)載流子的阻擋越來(lái)越明顯，直至一個(gè)阻擋極限，此時(shí)發(fā)生的負(fù)微分電阻最明顯，但相對(duì)于半導(dǎo)體中負(fù)微分電阻幅度，石墨烯中要小得多，因?yàn)樨?fù)能量區(qū)域內(nèi)，空穴載流子對(duì)電流的貢獻(xiàn)是不能忽略的。

實(shí)際的勢(shì)壘變化都不是階躍型的，而是有個(gè)過(guò)渡區(qū)，如文獻(xiàn)[17]所討論的那樣，但是由于過(guò)渡區(qū)的存在，負(fù)微分電阻效應(yīng)的幅度比方形勢(shì)壘情形下小了很多。關(guān)于如何增大負(fù)微分電阻效應(yīng)的設(shè)計(jì)與手段，人們?nèi)匀辉谔剿餮芯恐小?/p>

3 結(jié) 論

本文利用傳輸矩陣方法，對(duì)石墨烯典型的p-n結(jié)及方形勢(shì)壘納米結(jié)構(gòu)中的負(fù)微分電阻效應(yīng)進(jìn)行了研究。石墨烯p-n結(jié)中負(fù)微分電阻現(xiàn)象比傳統(tǒng)半導(dǎo)體中的幅度要小，原因在于石墨烯中Klein隧穿過(guò)程的存在使負(fù)能量范圍內(nèi)的空穴對(duì)電流也有貢獻(xiàn)。石墨烯納米方形勢(shì)壘中發(fā)生負(fù)微分電阻效應(yīng)的位置在費(fèi)米面附近，源于費(fèi)米面附近的載流子對(duì)電流的貢獻(xiàn)最大，勢(shì)壘寬度越大，對(duì)載流子的阻擋越大，因而負(fù)微分電阻效應(yīng)越明顯。這些結(jié)果對(duì)利用石墨烯高電子遷移率特性制備高頻器件具有參考價(jià)值。

參考文獻(xiàn)：

[1] NOVOSELOV K S，GEIM A K，MOROZOV S V，et al.Electric field effect in atomically thin carbon films[J].Science，2004，306（5696）：666-609.

[2] NOVOSELOV K S，GEIM A K，MOROZOV S V，et al.Two-dimensional gas of massless Dirac fermions in graphene[J].Nature，2005，438（7065）：197-200.

[3] GEIM A K.Graphene：status and prospects[J].Science，2009，324（5934）：1530-1534.

[4] CASTRO NETO A H，GUINEA F，PERES N M R，et al.The electronic properties of graphene[J].Reviews of Modern Physics，2009，81（1）：109-162.

[5] SZE S M，NG K K.Physics of semiconductor devices[M].3rd Ed.New Jersey：John Wiley & Sons，Inc.，2006.

[6] NGUYEN H C，NGUYEN V L.Tunneling of Dirac electrons through one-dimensional potentials in graphene：a T-matrix approach[J].Journal of Physics：Condensed Matter，2009，21（4）：045305.

[7] XU G J，WU B H，CAO J C.Alternating current Josephson effect in superconductor-graphene-superconductor junctions[J].Journal of Applied Physics，2011，109（8）：083704 -083709.

[8] GEIM A K，NOVOSELOV K S.The rise of graphene[J].Nature Materials，2007，6（3）：183-191.

[9] HEERSCHE H B，JARILLO-HERRERO P，OOSTINGA J B，et al.Bipolar supercurrent in graphene[J].Nature，2007，446（7131）：56-59.

[10] WEHLING T O，NOVOSELOV K S，MOROZOV S V，et al.Molecular doping of graphene[J].Nano Letters，2008，8（1）：173-177.

[11] XU G J，XU X G，WU B H，et al.The resonant tunneling through a graphene multiquantum well system[J].Journal of Applied Physics，2010，107（12）：123718-123724.

[12] XU G J，WU B H，XU X G，et al.Disorder effect on the transport properties of graphene quantum well structures[J].Journal of Physics：Condensed Matter，2010，22（43）：435301.

[13] DRAGOMAN D，DRAGMAN M.Negative differential resistance of electrons in graphene barrier[J].Applied Physics Letters，2007，90（14）：143111.

[14] NAM DO V.Comment on “Negative differential conductance of electrons in graphene barrier” [J].Applied Physics Letters，2008，92（21）：216101.

[15] KATSNELSON M I，NOVOSELOV K S，GEIM A K.Chiral tunneling and the Klein paradox in graphene[J].Nature Physics Letters，2006，2（9）：620-625.

[16] CHEN X，TAO J W.Design of electron wave filters in monolayer graphene by tunable transmission gap[J].Applied Physics Letters，2009，94（26）：262102.

[17] XU X G，XU G J，CAO J C.Electron tunneling through a trapezoidal barrier in graphene[J].Japanese Journal of Applied Physics，2010，49（8）：085201.

（編輯：劉鐵英）