基于GARCH族模型的葡萄酒投資指數的波動性分析

胡景煥

[摘 要]對葡萄酒投資市場的波動性進行研究，選取倫敦葡萄酒交易所（LIV-EX）發布的樣本區間為1988年1月至2013年11月的LIV-EX Fine Wine Investables Index月度數據，對FWI月收益率序列的平穩性、異方差性進行分析和檢驗。基于GARCH（廣義自回歸條件異方差，Generalized Auto-Regressive Conditional Heteroskedasticity）族模型來描述FWI的波動集聚性、敏感性及其杠桿效應。結果表明，FWI月收益率序列是平穩的，其指數波動具有高階ARCH效應，并且具有正向非對稱的反杠桿效應，但不存在ARCH in Mean效應。

[關鍵詞]葡萄酒投資指數；收益率；GARCH族模型；波動性；杠桿效應

[中圖分類號]F830.59 [文獻標識碼]A [文章編號]1671-8372（2015）03-0050-07

Study on the volatility of fine wine investable index based on GARCH family models

HU Jing-huan

（College of Transport and Communication， Shanghai Maritime University， Shanghai 201306， China）

Abstract：The monthly data of LIV-EX fine wine investable index（FWI）from Jan. 1988 to Nov. 2013 published by LIV-EX are selected in order to study the volatility of fine wine investment market and the stability as well as heteroskedasticity of its return series are analyzed and inspected. Then the volatility clustering， sensitivity and asymmetry of FWI are studied based on GARCH family models. Results show the return series of FWI is proved to be stable and there are high-level ARCH and anti-leverage effect on the fluctuation of fine wine， but there is no ARCH in mean effect.

Key words：fine wine investable index； rate of return； GARCH family models； volatility； leverage effect

改革開放以來，我國經濟快速發展，GDP連續多年保持兩位數的高增長，即使近幾年受經濟危機的影響增速略有回落，但仍然保持著適度的增長，人民的收入水平也有了很大提高。隨著富裕程度的不斷提高，人們也越來越關注儲蓄之外的其他個人投資渠道。總的來看，當前我國個人投資的主要領域有房地產、貴金屬、各類有價證券等。然而房地產的資金壓力大、貴金屬的不易變現及證券產品的高風險使得人們逐步將眼光擴展到其他投資渠道。在這其中，葡萄酒投資作為一種收益穩定的產品，越來越受到人們的關注。我國的葡萄酒消費群體中有相當一部分是高學歷、高收入的中青年成功人士，他們在品嘗美酒的同時，也逐漸認識到葡萄酒所蘊含的投資價值。

由于葡萄并非我國主要的消費農產品，國內對其價格的波動研究目前尚不多見，已有的文獻主要包括：孫偉等[1]運用坎德爾秩次相關分析的方法對我國葡萄的收購價格進行了研究，認為在多種因素影響的情況下，我國葡萄的收購價格波動幅度將越來越大；周力等[2]運用CMS模型研究了我國葡萄酒進口波動的成因，認為進口引力是左右我國葡萄酒進口貿易波動的首要原因。國外研究如Gregory等[3]分析了引起葡萄酒價格波動的幾個因素，包括天氣條件以及由于天氣條件引起的葡萄成分變化、主觀的品質評價和葡萄酒陳釀的時間等，認為不同品種的葡萄酒價格對于以上因素的敏感性各不相同。

更多的價格波動性研究則針對一般的農產品和食品。任全玉[4]以食品零售價格為研究對象，將不同食品進行合理分類，重點分析每類食品價格波動特點，并預測城市居民食品零售價格的走勢；李靜等[5]在分析了中國食品價格波動屬性的基礎上，具體研究了隨機因素對我國食品價格波動的沖擊效應和沖擊路徑；王振霞[6]對我國食品價格波動的原因進行了研究，認為城鄉居民人口結構的變化、脆弱的食品供給體系、不斷上漲的農業生產成本和通貨膨脹因素是引起食品價格波動的主要原因；馬敬桂等7]研究了農產品價格對CPI和食品價格波動的影響，認為農產品價格的同期沖擊影響對食品價格的沖擊較大，是引起食品價格波動的主要原因；余家鳳等[8]運用計量經濟學的方法對糧食產量和糧食價格之間的波動性進行了研究，認為糧價的變化對糧食產量變化的影響更為顯著。

葡萄酒投資作為一項新興的投資模式，尚有許多問題值得探究。本文將選取國際葡萄酒權威指數之一的LIV-EX Fine Wine Investables Index（下文簡稱FWI）作為研究對象，利用GARCH族模型對葡萄酒投資指數的波動性進行建模分析。

一、數據的選取及預處理

（一）FWI的背景介紹

FWI的構成來源于波爾多地區24所頂級酒莊大約200款葡萄酒的價格，該指數自1988年1月開始發布，比LIV-EX所發布的其他指數（如LIV-EX 50、LIV-EX 100等）都要早得多。由于所選取的葡萄酒大多為高檔酒，具有較高的投資價值，所以FWI可以反映葡萄酒投資市場的前景。指數以1982年Robert Parker發布的數據為基礎，主要以LIV-EX中間價進行計算，同時考慮葡萄酒的生產年份和產量，對于不同類型的葡萄酒給予不同的權重。為保證指數的公正性，其構成必須滿足下列三個條件：

（1）所選取的葡萄酒必須獲得行業認可品酒師95分以上的品質打分。

（2）所選取的葡萄酒不早于1982年，并且必須在市場上有銷售，以剔除少數不符合市場一般情況的珍藏美酒的因素。

（3）LIV-EX中間價是指某款酒在LIV-EX交易平臺上最高價與最低價的平均數；但如果某款酒在過去的30天內有成交，則按成交價作為當期的中間價；此外，每款酒的中間價都由評估委員會審核保證此價格是真實可靠的。

（二）數據的選取及描述性統計

本文選取由LIV-EX發布的從1988年1月到2013年11月的FWI月度數據，共311個觀測值作為研究對象。由于對時間變量進行自然對數處理能讓數據達到平滑的效果，使計算結果的擬合度更高，故首先對FWI序列進行自然對數處理，形成FWI對數序列，記為LNFWI，其走勢如圖1所示。

圖1 LNFWI月度序列圖

數據來源：www.liv-ex.com

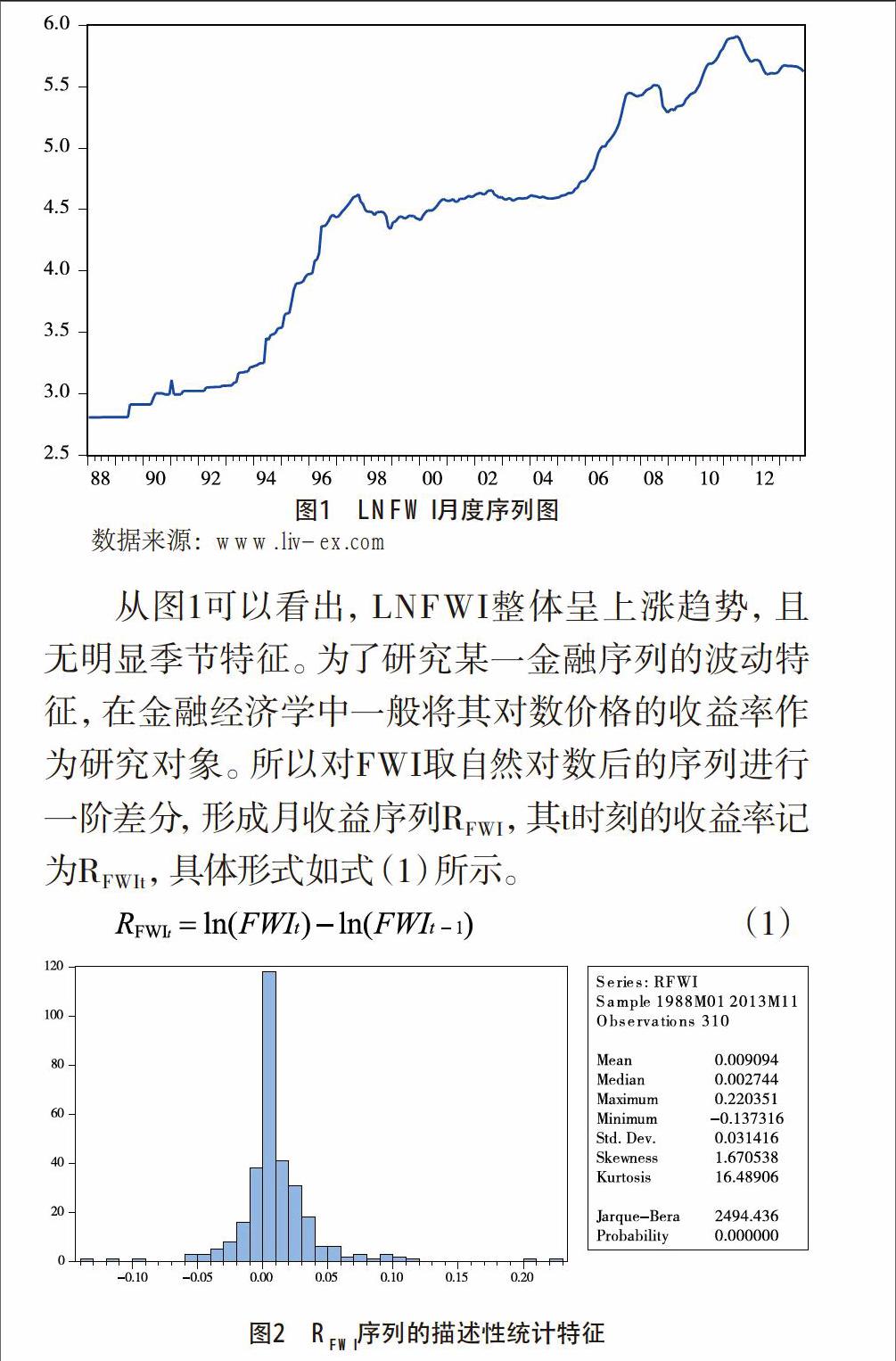
從圖1可以看出，LNFWI整體呈上漲趨勢，且無明顯季節特征。為了研究某一金融序列的波動特征，在金融經濟學中一般將其對數價格的收益率作為研究對象。所以對FWI取自然對數后的序列進行一階差分，形成月收益序列RFWI，其t時刻的收益率記為RFWIt，具體形式如式（1）所示。

（1）

圖2 RFWI序列的描述性統計特征

由圖2可以看出，該序列具有明顯的“寬尾”特征，Jarque-Bera檢驗的結果拒絕其屬于正態分布的假設；收益序列的均值為正，表明從長期來看，葡萄酒投資的平均收益為盈利水平，對其投資有利可圖；偏度系數大于0，表明該收益率序列具有右偏的非對稱性，說明該收益序列雖然長期為盈利水平，但從短期來看，虧損的可能性仍然不小；峰度系數遠大于3，表明FWI收益率序列有尖峰厚尾的特征，說明此收益序列有較大概率取到極端值，即發生劇烈波動的概率相對較高，有波動集群的特征。

（三）平穩性及自相關性檢驗

只有在一組時間序列平穩的情況下，時間序列隨機特征不再隨時間而變化，才能建模分析其未來的變化，所以對RFWI序列采用ADF（Augmented Dickey-Fuller）單位根檢驗，來驗證時間序列平穩性（見表1）。

表1 RFWI序列單位根檢驗結果

t-統計量 概率值*

-9.290573 0.0000

檢驗臨界值 1% level -3.451421

5% level -2.870712

10% level -2.571728

*macKinnon （1996） one-sided p-values.

從檢驗結果來看，單位根的mackinnon臨界值分別為-3.451421、-2.870712、-2.571728，t檢驗統計量為-9.290573，小于相應的臨界值，從而拒絕原假設，表明RFWI序列不存在單位根，是平穩序列。且由圖3可知，該序列圍繞零值上下隨機波動，沒有明顯向上或向下趨勢，但是存在較為明顯的極值，說明序列存在較大的波動性。

圖3 RFWI月度序列圖

接著對序列進行自相關性檢驗，發現序列的自相關函數拖尾，而偏自相關函數呈三階后截尾，初步判斷為AR（3）模型，首先由最小二乘法得到FWI月收益率序列RFWIt的擬合方程，如式（2）所示。

（2）

模型擬合系數的統計量見表2。

表2 RFWI序列AR（3）模型擬合系數統計量

變量 系數 標準誤 t-統計量 概率值

1 0.219380 0.056624 3.874294 0.0001

2 0.140377 0.057448 2.443532 0.0151

3 0.162036 0.056638 2.860890 0.0045

調整R2 0.065602

從表2中可以發現系數的相伴概率值均小于5%的顯著性水平，表明系數擬合狀況良好，但是調整R2值僅有0.065602，說明模型的解釋能力不強，可能存在其他影響模型解釋能力的因素。進一步對模型回歸方程的殘差序列進行LBQ檢驗，發現其自相關函數拖尾，而偏自相關函數呈25階截尾，表明FWI月收益序列回歸方程的殘差序列可能存在高階ARCH效應。進一步對殘差序列進行ARCH LM檢驗，通過引入輔助回歸方程來判斷是否存在ARCH效應，如式（3）所示。

（3）

式中，μt表示回歸方程在t時刻的殘差，εt為隨機擾動項。

通過檢驗，得到了在滯后階數q=25時的ARCH LM檢驗結果（見表3）。F檢驗和χ2統計量的相伴概率P值均小于5%顯著性水平，表明模型中的隨機誤差項不僅存在異方差，且存在高階ARCH效應，因此考慮利用GARCH族模型來刻畫其條件異方差，以消除序列中的異方差。

表3 RFWI殘差序列 ARCH LM檢驗結果

F-統計量 1.852344 概率值（25，256） 0.0097

χ2統計量 43.19767 概率值（25） 0.0133

二、基于GARCH族模型的波動性研究方法

大量實際數據表明，不同于一般的宏觀經濟變量，用來測度金融時間序列波動性的方差和協方差并非恒定不變，而是隨時間變化的，在方差的變化過程中，幅度較大的變化往往跟隨著幅度較大的變化，幅度較小的變化也往往跟隨著幅度較小的變化，即通常所說的波動聚集性[9]。

（一）ARCH-M模型

Engle于1982年引入條件方差的概念分析方差變化的原因，并提出ARCH模型，指出金融時間序列yt的條件方差ht會隨時間變化，因而可視ht為條件均值方程隨機誤差項μt滯后項的函數，即收益率的波動取決于以往的消息[10]。此外，一般金融理論認為金融資產的收益正比于其可能遭受的風險，較高的風險通常也會帶來較高的平均收益。為了描述這種現象，Engle等[11]將條件方差引入到均值方程中，構成ARCH-M模型，其數學模型可表示為：

（4）

式中，ɑ1，ɑ2，…，ɑq及ω為待估參數；μt服從q階的ARCH過程。由式（4）可知，對第i期收益率的波動影響由參數ɑi決定，q的值表示μt的某一波動情況持續的時間，因此該模型能夠刻畫市場的波動聚集性。

（二）GARCH模型

為解決ARCH模型中需要估計大量參數的難題，Bollerslev[12]提出了GARCH模型，把t時刻之前的條件方差加入到時刻t的條件方差函數之中，其對金融序列波動性分析和預測特別有效，GARCH（p，q）模型的基本表達式為：

（5）

式中ɑ1，ɑ2，…，ɑq；ω；β1，β2，…，βp為待估參數。ɑq，ω，βp均>0，并且GARCH（p，q）過程是平穩過程的充分必要條件是。此外，若p=0，則GARCH（p，q）過程退化為ARCH（q）過程；若p>1，q>1，則稱之為高階GARCH（p，q）過程，p，q的取值需根據擬合模型的AIC和SC值的大小來判斷。但在大多數實證研究中，考慮到模型的靈活性和簡約性，常用簡單的GARCH（1，1）模型擬合時間序列，基本公式為：

（6）

式中，ɑ表示前一期的波動情況，其大小反映出市場的變化對本期序列波動性影響的大小；β則表示前一期的波動情況對本期序列影響所持續時間的長短。

（三）EGARCH模型

GARCH模型雖然能夠解決高階ARCH模型的擬合問題，但仍然存在不少局限性。首先，為保證條件方差不為負，它要求各參數皆為正值，然而在實際應用過程中，這個條件常常難以得到滿足；其次，GARCH模型對波動性的描述是對稱的，它不能反映出序列波動的非對稱效應（也稱杠桿效應），即市場上“利好”與“利空”的消息對序列波動性影響的不一致性。為了刻畫序列波動性的非對稱效應，Nelson[13]提出了EGARCH（p，q）模型，用于刻畫市場“利好”“利空”消息對序列波動性影響的非對稱性，其數學表達式為：

（7）

式中，EGARCH（p，q）模型的條件方差ht是用指數形式表示的，它克服了GARCH模型對參數非負的限制，并且該模型引入了參數γ（杠桿因子），使模型可以表示非對稱效應（即在γ≠0的條件下，隨機干擾項取正值或負值時，會使ht發生不同程度的變化）。EGARCH模型通過杠桿因子γ反映正負干擾（“利好”和“利空”消息）對波動的非對稱影響：如果-1<γ<0，則表示一個負干擾（μt<0）引起ht的波動比相同程度的正干擾（μt>0）所引起的變化要大；如果0<γ<1，則表示一個正干擾（μt>0）引起ht的波動比相同程度的負干擾（μt<0）所引起的變化要大；如果γ=0，則表示ht對正負干擾的變化是對稱的。

三、基于GARCH族模型的FWI月收益序列波動性分析

（一）GARCH模型的確立

由于RFWI序列回歸方程的殘差項具有異方差性，且具有高階ARCH效應，使用ARCH模型對序列進行擬合時需設定較大的滯后階數，形式復雜，因此使用GARCH模型替代原來的ARCH模型。考慮到模型的簡約性，首先以GARCH-M（1，1）進行擬合，結果見表4。

表4 RFWI序列的GARCH-M（1，1）模型統計量

變量 系數 標準誤 t-統計量 概率值

ρ 5.269755 4.852858 1.085907 0.2775

ω 5.83E-05 9.40E-06 6.203274 0.0000

α 0.038071 0.009060 4.201879 0.0000

β 0.902356 0.014909 60.52598 0.0000

從表4中我們可以得出以下結論：ω、α、β這三項參數估計的t統計量非常顯著，其相應的概率值也非常小，且ARCH項和GARCH的各項系數估計值之和ɑ+β=0.940427<1，說明GARCH-M（1，1）為平穩過程，模型能夠反映出FWI月收益率序列RFWI的異方差性，同時也說明RFWI序列具有波動集群的性質；但均值M的參數ρ的相伴概率未能通過驗證，表明RFWI序列不存在ARCH in Mean效應，即對于FWI而言，其預期收益與風險可能不一定成正比關系，并非意味著預期風險越大，收益就越高。

剔除ARCH in Mean的因素后，重新對RFWI序列建立GARCH（1，1）模型（見表5）。

表 5 RFWI序列的GARCH（1，1）模型統計量

變量 系數 標準誤 t-統計量 概率值

ω 0.000868 5.00E-05 17.36441 0.0000

α 0.369327 0.090313 4.089428 0.0000

β -0.212812 0.049040 -4.339555 0.0000

此時ω、α、β這三項參數估計的t統計量非常顯著，其相應的概率值也非常小，且ARCH項和GARCH的各項系數估計值之和ɑ+β=0.156515<1，說明GARCH（1，1）為平穩過程。雖然此處GARCH項的參數β為負，但對本例而言，其結果并不影響條件方差ht仍然為正，所建的模型能較好地擬合RFWI序列，其條件方差序列圖如圖4所示。

圖4 GARCH（1，1）條件方差序列圖

（二）EGARCH模型的確立

為了刻畫出FWI波動的非對稱性，即FWI對不同外部消息刺激的反應程度，在上文GARCH（1，1）模型的基礎上進一步運用EGARCH模型對其月收益率序列的RFWI的波動性進行分析，建立EGARCH（1，1）模型（見表6）。

表6 RFWI序列的EGARCH（1，1）模型統計量

變量 系數 標準誤 t-統計量 概率值

ω -11.43678 0.482245 -23.71573 0.0000

α 0.367793 0.053763 6.840965 0.0000

γ 0.145432 0.043124 3.372407 0.0007

β -0.559252 0.065038 -8.598800 0.0000

從表6可以看出，ω、α、β、γ參數估計的t統計量非常顯著，其相應的概率值也非常小，表明EGARCH（1，1）模型擬合情況良好。從以上數據分析可見，γ=0.145432，說明FWI的月收益率序列具有非對稱的杠桿效應，且外部市場“利好”消息對該序列波動的影響程度大于“利空”消息的影響程度。當葡萄酒投資市場出現“利好”消息時，非對稱效應參數ɑ+γ=0.513225，即“利好”消息會給FWI月收益率的條件方差帶來0.513225倍的沖擊；而當市場出現“利空”消息時，非對稱效應參數ɑ-γ=0.222361，即“利空”消息會給FWI月收益率的條件方差帶來0.222361倍的沖擊。可見葡萄酒投資市場的波動具有正向非對稱，市場上的“利好”消息比等量的“利空”消息對葡萄酒投資市場產生的沖擊明顯更大，說明雖然葡萄酒投資市場的波動具有非常明顯的非對稱性，且“利好”消息對指數波動的影響要遠大于“利空”消息的影響。

四、結果分析

（一）基于GARCH（1，1）模型的結果分析

從GARCH（1，1）建模的結果來看，FWI的月收益序列在1991、1994、1996和2008年分別有四個比較大的波動，具體分析如下：

1.1991和1994年。從表7可以看出，法國葡萄酒的需求量從1986年開始一直到1995年左右一直在下降，而其產量在經歷20世紀80年代后期的大幅下降后從1991—1992年開始回升（雖然缺乏1991和1992年的產量數據，但是從1991—1995年的平均產量和1993—1995的產量中可以看出，法國葡萄酒的產量在1991—1995年處于上升軌道）。受供需不平衡的影響，在1991和1994年左右法國葡萄酒的平均價格有兩次較為明顯的下跌行情（如圖5所示），尤其是1994年，跌至近些年的底點。受價格下跌的影響，FWI在這兩年附近出現了劇烈的波動。

表7 1986-1998年法國葡萄酒生產和消費數據（單位：hl）

1986-

1990年 1991-

1995年 1993年 1994年 1995年 1996年 1997年 1998年

產量 64641 52886 52059 53325 54354 57047 53561 52671

消費量 41715 37310 37354 36663 36515 34795 35500 35800

數據來源：OIV

圖5 1988-2000法國葡萄酒價格（單位：法郎/hl）

數據來源：OIV

2.1996年。在1996年葡萄酒的消費量進一步下滑而產量繼續上升的情況下平均酒價反而攀升到近些年的高點，其背后的主要原因是增加的產量主要為了滿足出口的需要。據OIV統計[14]，法國葡萄酒1996—2000年的平均出口量較1991—1995年增長了33%，其主要原因是以中國為首的新興國家葡萄酒需求大幅增長。以中國為例，其1995年的葡萄酒消費量較1994年上漲了43%，2000年比1996年更是增長了近80%，而其自身產量到了1999年才出現比較大的漲幅，顯然在1995—1998年產量和消費量之間的缺口需要由進口酒來填補，其中法國則是最主要的來源。高漲的出口熱情拉動了葡萄酒價格的上漲，也使FWI出現了較為明顯的波動。但隨之而來的東南亞金融危機最終影響到全球經濟，造成葡萄酒價格在1997—1998年處于較低的水平，FWI受其影響，也出現了小幅但比較明顯的波動。

3.2008年。據全球主要的商業拍賣行發布數據顯示，2007世界范圍內的精品葡萄酒拍賣額比2006年上升了25%，達到了3.1億美元，美元匯率的下跌使美國占主導地位的競標吸引了很多買家。2008年前三季度，各大拍賣行交易額均呈增長趨勢，珍稀葡萄酒很好地抵御了經濟衰退的影響。然而10月之后，全球金融市場徹底崩潰，葡萄酒市場也不可避免地跟著迅速跌落。2008年全球拍賣行精品葡萄酒交易額從上一年的3.1億美元降至2.76億美元，不過與主要的股指相比，8%的跌幅并不算很大，這從另一方面也表現出葡萄酒投資具有一定的抵御風險性。

而從日常葡萄酒的價格來看，受金融危機的影響，法國葡萄酒的價格跌至近1994年以來的最低點。但這并非完全是由經濟危機造成的，2004年全球葡萄酒產量過剩達到最高點（如圖6所示），之后葡萄酒價格便不斷走低，并一直在低位波動，而之后受金融危機的影響在2008年達到最低，不過此后便開始逐步回升（如圖7所示）。本文認為造成這一現象的原因在于葡萄酒在西方國家屬于日常消費品，具有較強的剛性需求，其價格受供需平衡的影響要大過經濟危機的影響。

圖6 世界紅酒產銷差額（單位：Mhl）

數據來源：OIV

（二）基于EGARCH（1，1）的FWI杠桿效應分析

從圖1可以看出，FWI從1992年開始有上升的趨勢，而在1994—1996年幾乎呈現垂直上升，正是受1992年下半年開始的葡萄酒價格下跌的影響；2004—2008年和2009—2011年也出現了同樣的現象。本文分析認為葡萄酒價格下跌對FWI的投資而言并非是“利空”的壞消息，反而代表出現了一個可以低價買入的投資好時機，是“利好”消息。同時也可以發現，1997年開始的東南亞金融危機及2008年下半年出現的全球經濟危機對FWI波動的影響并沒有其受葡萄酒價格下降帶來的影響更為明顯，這與一般認為的經濟危機可能對金融指數帶來較大波動影響并不相符，其原因在于FWI的杠桿系數γ為正，且ɑ+γ值與ɑ-γ值相差近兩倍，結果造成其對“利空”消息的敏感度遠不如對“利好”消息的敏感度。

圖7 1997-2008法國葡萄酒價格（單位：歐元/hl）

數據來源：OIV

五、結束語

1.從FWI的對數序列LNFWI月序列圖（圖1）中可以看出，對于長期投資而言，FWI具有明顯的上漲趨勢。進一步分析其月收益率RFWI序列的基本統計概況可以發現，FWI具有一般金融收益序列的非正態分布、尖鋒厚尾、異方差和波動集群等特征。

2.使用AR（3）模型能較好地擬合RFWI序列，但進一步使用GARCH-M（1，1）模型研究發現其不存在ARCH in Mean效應，這不符合一般金融序列的收益與風險成正比的普遍現象。本文認為雖然FWI是一種金融衍生產品，但由于葡萄酒本身在西方國家是一種日常消費品，具有一定的剛性需求，FWI波動不像其他金融產品那樣對經濟的變化敏感。去除Mean的因素后使用GARCH（1，1）模型便能較好地擬合FWI的波動特征，發現其在1991、1994、1996和2008年分別存在四個比較大的波動，但與股票債券等高風險金融產品相比，FWI的波動幅度明顯較小。

3.使用EGARCH（1，1）模型擬合了FWI月收益序列的杠桿效應，反映出“利好”和“利空”消息對FWI的影響程度。研究發現葡萄酒投資市場的波動具有明顯的非對稱效應，市場對“利好”消息的敏感度遠大于對“利空”消息的敏感度，表現出反杠桿效應，這表明葡萄酒投資市場抵御風險的能力較強，一般的“利空”消息并不會對葡萄酒投資市場造成較大的沖擊；相反，若是受“利好”消息的影響，則葡萄酒投資市場會受到正向的沖擊，帶動指數上漲，從這點來看，葡萄酒的投資具有廣闊的前景。正如倫敦國際葡萄酒交易所負責人詹姆斯·邁爾斯所說：“投資葡萄酒并非萬能藥，你必須睜大眼睛。在經濟市場長期混亂的局面中，葡萄酒的價格也會下降。但是這一下降不像債券、股票、地產市場那樣萎靡，葡萄酒的前景看上去仍很強勁。”

孫偉，周志堅，穆維松.葡萄收購價格的波動特征分析[J].中外葡萄與葡萄酒，2011（7）：69-71.

周力，應瑞，瑤江艷.我國葡萄酒進口貿易波動研究—基于CMS模型的因素分解[J].農業技術經濟，2008（2）：25-31.

Gregory V Jones，Karl-Heinz Storchmann.Wine market prices and investment under uncertainty： an econometric model for bordeaux Crus classes[J].Agricultural Economics，2001，26（2）：115-133.

任全玉.基于價格指數的食品價格波動分析[J].中國商貿，2012（22）：90-91.

李靜，楠玉.我國食品價格波動沖擊路徑的隨機因素分析[J].經濟經緯，2013（2）：28-32.

王振霞.我國食品價格波動原因及價格穩定機制研究[J].財貿經濟，2011（9）：113-119.

馬敬桂，黃普.農產品價格對CPI和食品價格的沖擊效應分析—基于VAR模型的實證分析[J].長江大學學報（自然科學版），2011，8（9）：256-260.

余家鳳，孔令成，龔五堂.糧食產量與糧價波動關系的再研究[J].經濟問題，2013（1）：108-111.

Tsay R S.金融時間序列分析[M].潘家柱，譯.北京：機械工業出版社，2006.

Engle R F.Autoregressive conditional heteroscedasticity with estimates of the variance of UK inflation[J].Econometrica，1982（50）：987-1008.

Robert F Engle，David M Lilien，Russel P Robins.Estimating time varying risk premia in the term structure：the ARCH-M model[J].Econometrica，1987，55（2）：391-407.

T Bollerslev.Generalized auto regressive conditional heteroskedasticity[J].Journal of Econometrics，1986（31）：307-207.

Nelson D B.Conditional heteroskedasticity in asset returns：a new approach[J].Journal of Econometrics，1991，59（2）：347-370.

G Dutruc-Rosset.The state of vitiviniculture in the world and the statistical information in 2000[R].Belgique：International Office of Vine and Wine，2001.

[責任編輯 王艷芳]