基于干擾抑制和非線性摩擦力補償的速度環PI控制器抗飽和設計

王慎航，王云寬，胡建華，秦曉飛，鄭軍，劉娜

?

基于干擾抑制和非線性摩擦力補償的速度環PI控制器抗飽和設計

王慎航，王云寬，胡建華，秦曉飛，鄭軍，劉娜

(中國科學院大學自動化研究所，北京，100190)

針對永磁同步電機速度調節器積分飽和導致動態品質變差的問題，提出一種新型的抗飽和(AW)設計方法。該AW方法首先把模型的不確定性視為系統的干擾；然后為了改善系統性能和提高抗干擾能力，在比例積分(PI)控制策略基礎上，對速度環設計一種基于摩擦模型補償和擾動觀測補償的復合控制方法；最后把PI控制器退飽和后從比例(P)模式重新進入PI模式的系統響應看作是帶有初始值的系統響應，同時利用時域下的系統誤差動態響應方程推導出系統無超調的誤差和積分條件，當系統進入飽和時，系統以最大加速度運行，直到滿足條件才重新進入PI模式，并給積分賦初始值。研究結果表明：該方法確保退飽和系統的優良的動態性能和無超調運行。與現有條件積分方法及其改進的方法相比，仿真和實驗結果驗證該新型AW 設計的可行性及優越性。

永磁同步電機(PMSM)；抗積分飽和；PI速度控制器；非線性摩擦力；干擾觀測器；無超調

永磁同步電機(PMSM)以其體積小、功率密度大、低速輸出轉矩大、效率高、維護簡單而被廣泛應用于數控，軌道車輛等中[1]。PI控制由于其控制算法簡單、魯棒性好、易于實現等優點，已經被廣泛的應用于永磁同步電機交流調速系統。電流環作為調速系統內環，保證了系統的動態響應速度，而速度環作為外環給電流環產生電流指令。速度環給出的電流指令值往往要進行限幅，因為電機最大電流限制、逆變器保護以及驅動裝置過熱保護的要求。由于PI控制器的設計往往是在系統線性區而忽略了飽和的限制。因此，當系統飽和時，PI控制器往往失去了調節的作用，并導致系統大的超調、調節時間長、震蕩甚至不穩定問題，這種現象稱為積分飽和現象[2?4]。為了克服積分飽和現象，許多抗飽和技術被提出，其中有一些運用非線性方法抑制飽和現象[5?7]，但是這增加了系統的復雜度，失去了PI控制器簡單易實現的特點。因此，典型的抗積分飽和做法是增加積分飽和補償裝置。實質上，傳統的抗飽和方法主要分為2類[8]：一類是條件積分方法，另一類是反計算方法。條件積分方法是當控制器飽和時關閉積分，當控制器退出飽和時重新開啟積分。反計算方法是將控制器的輸出與被控對象的輸入之差構成反饋支路來減小積分量的輸入，達到抑制積分飽和現象的目的。為了確保系統退飽和后無超調的動態品質，一些學者進一步地提出了其他控制技術。Choi等[9]針對有2個負實數極點的調速系統提出來一種方法，具體是當系統從P模式到PI模式轉換時，賦予積分初始值來消掉系統的1個極點，系統成為一階系統，保證了系統退飽和后響應的無超調。Hwi等[10]采用積分穩態的預測值作為PI模式重啟時的積分初始值來抑制超調。同時，在現有的系統建模方法中，往往忽略了系統的摩擦力、外界干擾及模型的不匹配，把模型建立成線性系統模型，并在此模型的基礎上設計了AW方法。很顯然，這種設計思想雖然在理論上能夠取得理想的結果，但是由于摩擦力[11?12]和干擾[13?14]的影響，控制效果也將大幅下降。為了解決現存方法的問題，本文作者提出一種新穎的AW算法。該方法首先改變傳統的建模方法，考慮基于非線性摩擦力的補償和干擾抑制，有效地抑制模型的不確定性。然后把退飽和重新進入PI模式的系統響應看作是帶有初始值的系統響應，同時利用時域下的系統誤差動態響應方程推導出系統無超調的誤差和積分值條件，當系統重新進入PI模式時給積分賦初始值。該方法確保退飽和系統的優良的動態性能和無超調運行。與現有方法相比，仿真和實驗結果驗證該新型AW 設計的可行性及優越性。

1 基于摩擦力補償和干擾抑制的誤差模型建立

為了快速地跟隨速度環誤差指令，在伺服系統設計中往往要求電流環的帶寬遠大于速度環的帶寬，這樣電流內環就可看做1個常數放大器。不考慮系統干擾和噪聲，那么速度環伺服系統可以簡化為一階系統

其中：=Ti，為控制力矩；T為力矩常數；為電機轉速；L為負載力矩；為摩擦力，包含線性和非線性摩擦力。與傳統的建模方法相比，式(1)增加了非線性摩擦力的建模，顯然這增加了系統的非線性因素，但它更能準確地描述系統的動態響應，這有利于基于模型的飽和算法更加準確地實現。

1.1 摩擦力的補償

Stribeck摩擦模型[11]在動態補償中應用比較廣泛，能夠有效地描述線性和非線性摩擦力，是由庫侖力、黏性摩擦力和靜態摩擦力組成

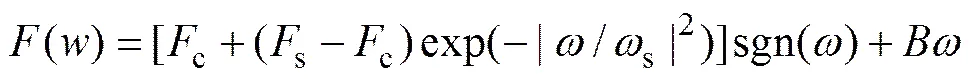
式中：c為庫侖摩擦力；s為靜態摩擦力；為黏性摩擦力因數；為潤滑參數；為電機轉速。若控制系統中控制輸入量按照式進行摩擦力的補償，則

其中：0為摩擦力補償輸入；為新的控制輸入量。將式代入式，系統中將沒有摩擦力的非線性特性，得到線性的關系

1.2 基于干擾觀測器(DOB)的干擾抑制

為了抑制外部干擾以及高頻噪聲，在反饋控制的基礎上進一步地加入了干擾觀測器，如圖1所示，其中：，和分別為干擾、噪聲和干擾的估計值。為了便于問題的分析和模型的建立，本文將系統的模型不匹配歸于系統的干擾[13]，那么系統對象可建立為=P。其中：為實際控制對象；P為名義模型對象。進而可得到控制外環傳遞函數：

其中：和分別為外環靈敏度和補靈敏度函數；為外環控制器；為濾波器。式說明干擾回路的加入對于外環的輸入輸出控制沒有影響，這也從理論上說明了外環的設計完全不受干擾觀測器的影響。但從式和可以看出和同時影響著系統干擾對外環的輸出，因此，在設計干擾觀測器時應同時兼顧和的作用。本文采用低通濾波器