列車撞擊荷載下盾構隧道雙層襯砌管片結構的動力響應特性

晏啟祥，李彬，張蒙，陳誠

?

列車撞擊荷載下盾構隧道雙層襯砌管片結構的動力響應特性

晏啟祥1，李彬1，張蒙2，陳誠1

(1. 西南交通大學交通隧道工程教育部重點實驗室，四川成都，610031；2. 中鐵工程設計咨詢集團有限公司，北京，100020)

通過建立三維列車編組撞擊有限元模型，獲得不同列車編組、列車行駛速度、斜向撞擊角度下列車的脫軌撞擊荷載時程曲線。采用HHT時間積分法和混凝土塑性損傷模型，研究雙層襯砌在不同列車撞擊速度和撞擊角度下，管片襯砌的應力、變形、速度、加速度、拉壓損傷因子及損傷面積等動力響應。研究結果表明：列車撞擊荷載主要與列車行駛速度、斜向撞擊角度以及列車編組數量有關；撞擊力時程曲線在一定條件下出現第2個峰值，動力響應隨著列車撞擊速度和撞擊角度的增大而增大，受拉損傷平均值及其最大值均大于受壓損傷平均值和最大值，得出拉壓損傷與撞擊速度和角度的相互關系。

雙層襯砌；列車撞擊荷載；管片襯砌結構；動力響應；拉壓損傷

目前，國內高速列車的運行安全已日益引起人們的高度關注，高速列車可能脫軌撞擊有較大彎道和坡道的盾構隧道并導致隧道結構被破壞，這一威脅已在我國高速鐵路建設背景下逐漸顯現。國內公路盾構隧道采取防撞墻、防撞墩等非隧道本體結構來應對車輛撞擊問題。對于整體質量大、速度高的列車編組，通常采用在管片襯砌內部模筑二次襯砌形成的雙層襯砌結構加以應對，如設計目標速度為350 km/h的廣深港客運專線獅子洋隧道、滬通鐵路黃浦江水下隧道及論證中的瓊州海峽跨海通道隧道方案等。盡管國內已經認識到水下盾構隧道管片襯砌遭受列車碰撞的可能性，并采取雙層襯砌的防撞措施，但防撞襯砌的設計基本靠經驗進行，缺乏應有的理論和實踐依據。由于目前國內缺乏對雙層襯砌撞擊動力學及其防撞效果的研究，尚未揭示不同列車撞擊荷載下二次襯砌對管片襯砌保護程度，因此，開展不同列車撞擊荷載下盾構隧道雙層襯砌管片結構的動力響應特性的研究顯得很有必要。國內外近20 a來一直在研究列車被動防護技術，1997年美國制定列車撞擊相關安全規范，對單節車輛與剛性墻撞擊到列車多體撞擊進行大量研究[1]；田口真[2]在美國科羅拉多州進行單臺整車的撞擊試驗；姚松等[3]模擬薄壁結構的車輛吸能部件碰撞，并將研究成果成功應用在吸能列車上，取得較好的效果；房加志等[4]利用ABAQUS有限元軟件探討高速列車鋁合金材料的耐撞性。上述研究基本都是關注車輛的耐撞性，通過事先假定撞擊荷載進行研究，目的是開展列車的防撞性設計以保護車上人員的安全。在混凝土或鋼筋混凝土材料的沖擊力學研究方面，目前主要集中在結構混凝土材料動態本構模型上，如李兆霞 等[5?6]提出鋼筋混凝土材料含有損傷的黏塑性本構模型；Burlion等[7]提出一種基于損傷與塑性相耦合的本構模型。由于缺乏對混凝土材料在沖擊荷載作用下破壞機制的全面認識，至今仍未有一種普遍接受的材料本構模型。由于南水北調總干渠穿黃隧洞初步設計擬采用雙層襯砌，我國在前期開展了少量有關雙層襯砌力學特性的研究，并提出雙層襯砌抗壓縮模型、局部抗彎模型和抗剪壓模型等[8]，但國內對雙層襯砌力學特性的認識和二次襯砌的具體作用依然沒有一致的看法[9?11]。目前，國內列車與隧道的相互作用主要在研究隧道斷面對高速列車風的影響以及高速列車風對隧道及其內部設施的影響上，如施成華等[12]研究高速鐵路隧道內列車風對接觸網安全性的影響，尚未有列車脫軌碰撞荷載和撞擊荷載下雙層襯砌盾構隧道的動力特性及其損傷評估的相關成果。鑒于此，本文作者基于動力學以及損傷分析理論，建立三維列車編組有限元模型，獲得不同因素影響下的列車撞擊荷載曲線，研究荷載作用下雙層襯砌盾構隧道的動力響應，以揭示二次襯砌對隧道的保護作用。

1 動力學求解及損傷分析理論

采用Hilber，Hughes和Taylor時間積分法(簡稱為HHT法)[13]求解列車脫軌撞擊結構動態響應。HHT時間積分法是由最基本的Newmark時間積分法推演而來，運用隱式HHT時間積分法可有效解決結構非線性動態問題，其對任意時間步長都具有很好的穩定性。將結構體系時刻的達朗伯爾力，與，時刻靜力的加權平均值相平衡，其中為計算中某一時刻，為時間推進計算中下一時刻，得HHT時間積分法平衡方程及其位移和速度如下：

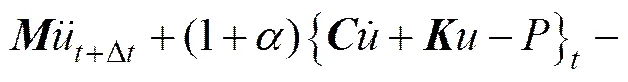
式中：為質量矩陣；為阻尼矩陣；為剛度矩陣；為列車撞擊荷載；，和分別為系統位移、速度和加速度。和由權重因子決定：

式中：t為拉損傷因子；為應變與峰值應變之 比；，為拉應力對應的拉應變，為與峰值拉應力對應的峰值拉應變，；，t為峰值拉應力。

在受壓條件下，壓損傷因子c為

式中：c為壓損傷因子；，為壓應力對應的壓應變，為與峰值壓應力對應的峰值壓應變，，c為峰值壓應力；；。

對于C50混凝土的管片襯砌，其彈性模量為 34 500 MPa，泊松比為0.2，材料進入塑性后應力與非彈性應變、損傷因子與非彈性應變的相互關系見表1。

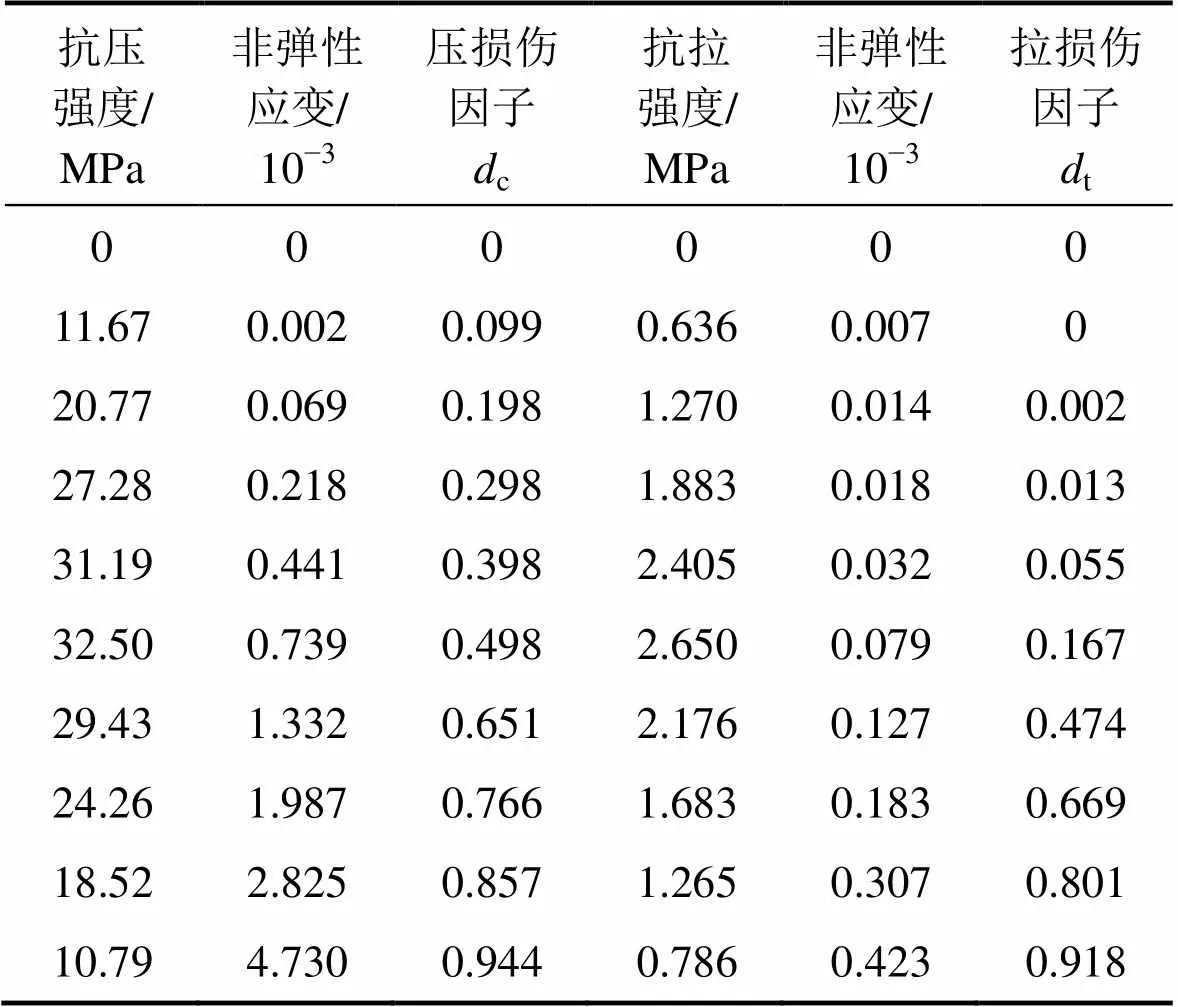
表1 管片混凝土的拉壓損傷演化參數

2 列車撞擊荷載的確定

由于國內尚未有列車脫軌實例和相關試驗數據，因此，采用數值分析法近似獲取列車撞擊荷載，通過建立簡化的列車?剛性墻撞擊三維模型得到近似的撞擊力時程曲線。列車編組的材料參數如表2所示，采用薄殼單元建立鋁合金型材車體模型，用嵌入泡沫芯材和玻璃鋼等型材實現近似等效的車體剛度和相似的質量分布。列車編組車廂之間的連接掛鉤用非線性彈簧來模擬，彈簧的剛度和阻尼參數根據國產密接式車鉤緩沖裝置力學性能曲線確定[15]，彈簧剛度參數和阻尼參數分別為2 000 kN/m和40 kN?s/m。

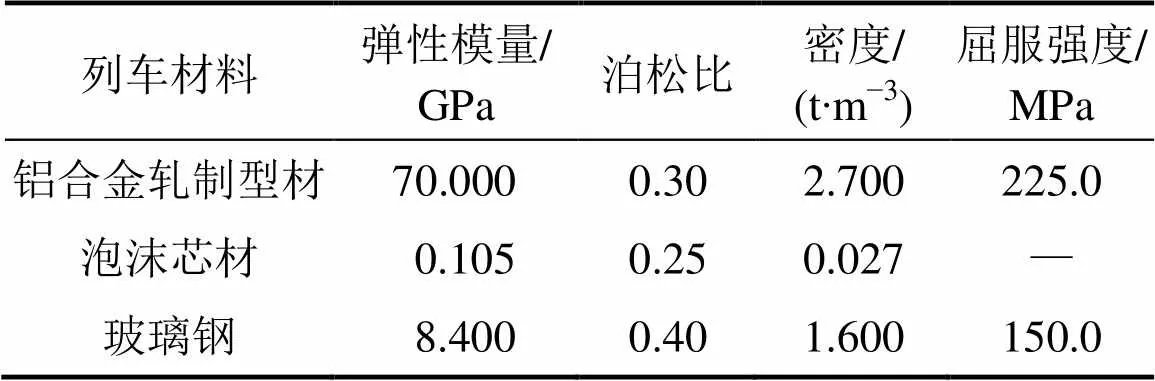
表2 列車材料參數

采用8，12與16節這3種編組數量，50，100，150，200，250和300 km/h共6種撞擊速度，5.0°，7.5°，10.0°，12.5°，15.0°和17.5° 這6種撞擊角度構成的108種交叉組合對相應撞擊力時程進行分析。圖1所示為8，12和16節3種編組的列車在300 km/h撞擊速度、斜向撞擊角度為17.5°的撞擊剛性墻的撞擊力時程曲線。由圖1可以看出：3種編組的撞擊力時程曲線趨勢相同，數值接近，相同撞擊速度和撞擊角度下3種編組的撞擊力時程曲線表現出相同的特點，說明列車編組的撞擊力時程曲線主要與前幾節車廂有關，當列車編組數超過5節后，與列車編組數的相關性減小，原因在于撞擊過程極短，后續車輛的慣性力通過車鉤傳遞到機車撞擊部位時已經是撞擊過程的后段，難以形成疊加效應。由于難以羅列108種交叉組合的列車撞擊時程曲線，只代表性給出8節編組列車以12.5°和不同速度斜向撞擊的撞擊力時程曲線，以及8節列車編組以200 km/h和不同撞擊角度撞剛性墻獲取的近似撞擊力時程曲線，分別如圖2和圖3所示。

從圖2和圖3可以看出：在同一撞擊角度下，隨列車撞擊速度增大，撞擊力時程曲線上的撞擊力整體增大，其撞擊持續時間也越長；在同一撞擊速度下，斜向撞擊角度越大，其撞擊力時程曲線上的撞擊力也越大。撞擊力在撞擊瞬間急劇增大并達到最大值，隨后急速減小并震蕩持續波動一定時間，當角度超過12.5°或列車速度超過200 km/h時，撞擊力時程曲線還會出現第2個峰值，撞擊過程作用時間根據撞擊速度和角度的不同而不同，但基本處于25~40 ms。

列車編組/節：1—8；2—12；3—16

撞擊速度/(km?h?1)：1—50；2—100；3—150；4—200；5—250；6—300

角度/(°)：1—5.0；2—7.5；3—10.0；4—12.5；5—15.0；6—17.5

圖4 在12.5°撞擊角度下不同撞擊速度的撞擊力第1個峰值

圖5 在200 km/h時不同撞擊角度的撞擊力第1個峰值

3 不同撞擊荷載下管片襯砌的動力效應

在獲取不同列車行駛速度和撞擊角度近似撞擊荷載的基礎上，選取國內某水下盾構隧道盾構管片襯砌為分析對象，開展雙層襯砌外部管片襯砌的撞擊動力效應分析。通過對比不同撞擊力作用下管片襯砌的動力響應，分析撞擊速度和撞擊角度對管片襯砌動力響應的影響。撞擊力時程曲線選用8節編組在12.5°撞擊角度下不同撞擊速度，以及8節編組在200 km/h撞擊速度下不同撞擊角度。將獲得的撞擊力按實際撞擊位置和作用范圍以平均面力的近似形式施加在二次襯砌上。該隧道設計采用雙層襯砌結構型式，隧道外徑為10.30 m、內徑為8.74 m、管片厚度為0.48 m、幅寬為2.00 m、混凝土二次襯砌厚度為0.30 m，所襯砌斷面如圖6所示。隧道周邊圍巖為第4系上更新統Q3和全新統Q4沉積物，主要由砂性土、風化泥質粉砂等組成。

他無意與小涵爭辯。“小涵理論”有著眾多的支持者，他甚至贊成其中的某些觀點。不能相愛，還能相處。如果連相處都成為困難的事情，婚姻也就隨之解體。他和小涵的相處是靜態相處，沒有過多糾纏不清的熱度。小涵說要外出，他會奉獻一句玩得開心；他告訴小涵要出門，小涵會回一句，我在家，你放心去吧。半夜回來，更不需要多言，他們各有各的房間。

隧道圍巖采用M?C彈塑性本構關系，管片襯砌和二次襯砌采用前述的塑性損傷本構模型。模型邊界采用彈簧?阻尼器系統人工邊界，用連續分布的并聯彈簧?阻尼器系統表示。管片襯砌混凝土采用C50混凝土，管片襯砌環間接頭采用抗彎剛度等效的原則，通過弱化環間10 cm長混凝土彈性模量的方式近似模擬。砂性土、風化泥質粉砂、管片襯砌和二次襯砌分析參數如表3所示。圍巖襯砌分析模型長×寬×高為90 m×60 m×60 m，如圖7所示。

圖6 盾構隧道雙層襯砌

表3 基本材料參數

(a) 有限元三維模型網格圖；(b) 人工邊界等效彈簧?阻尼器系統

選取管片襯砌內側一系列點作為數值分析特征點分析。以二次襯砌撞擊區域中心橫向水平對應的管片襯砌點為基點，水平縱向前后兩側等距離各取7個數值分析提取點，間距為0.5 m，數值分析提取點1~15位置如圖8所示，其中，撞擊中心點對應管片襯砌編號為8，模擬列車從左至右行駛并斜向12.5°撞擊在二次襯砌上。

圖8 數值分析提取點示意圖

3.1 不同撞擊速度

圖9所示為撞擊角度為12.5°時不同撞擊速度下管片襯砌各數值提取點的峰值應力、位移、速度和加速度圖。由圖9可以看出：隨著撞擊速度的增大，管片襯砌峰值應力、位移、速度和加速度隨之增大，在時速300 km/h的條件下，管片襯砌峰值應力、位移、速度和加速度最大值分別達34.5 MPa，6.75 mm，1.85 m/s和3 450 m/s2；隨著撞擊速度的增大，各峰值不斷增大，但增幅在每個速度區間有所不同。

相同撞擊速度下，各數值提取點的峰值位移、速度和加速度以撞擊區域中心前方1.0 m的位置10最大，而在150 km/h以下時，峰值應力以撞擊點中心區域位置8最大，當撞擊速度大于150 km/h時，峰值應力可能出現在前方位置9或后方位置7。

圖10所示為不同撞擊速度下管片襯砌受壓、受拉損傷平均值，受壓、受拉損傷面積與撞擊速度的關系。從圖10可以看出：受壓損傷平均值隨撞擊速度的增長表現為平穩增長，而受拉損傷值在50~100 km/h時對撞擊速度較為敏感，速度從50 km/h增大到100 km/h時，受拉損傷平均值均急劇增大，但當撞擊速度為100~300 km/h時增長不明顯；受拉損傷面積隨著撞擊速度的增大表現為較平穩的增長；受壓損傷面積在50~100 km/h時對撞擊速度較為敏感，當撞擊速度從50 km/h增大到100 km/h時，受壓損傷面積急劇增長，但當撞擊速度為100~300 km/h時，受壓損傷面積增長較緩慢。總體而言，受拉損傷平均值和受拉損傷面積隨著撞擊速度的增大迅速上升到較高水平，之后緩慢增長，而受壓損傷平均值和受拉損傷面積則隨著撞擊速度的增大而慢慢增長。

(a) 應力；(b) 位移；(c) 速度；(d) 加速度撞擊速度/(km?h?1)：1—50；2—100；3—150；4—200；5—250；6—300

(a) 損傷平均值；(b) 損傷面積

1—受壓損傷；2—受拉損傷

圖10 管片襯砌拉壓損傷與速度的關系

Fig. 10 Relationship between tensile and compressive damage of segment lining and impact velocity

3.2 不同撞擊角度

(a) 應力；(b) 位移；(c)速度；(d)加速度

撞擊角度/(°)：1—5.0；2—7.5；3—10.0；4—12.5；5—15.0；6—17.5

圖11 不同撞擊角度下管片襯砌各提取點峰值應力、位移、速度和峰值加速度

Fig. 11 Peak stress, peak displacement, peak velocity and peak acceleration of segmental lining extraction point at different impact angles

在相同撞擊角度下，各數值提取點的峰值位移、速度和加速度以撞擊區域中心前方1.0 m的位置10最大，而峰值應力在10.0°以下時以撞擊點中心區域位置8最大，當撞擊角度大于10.0°時，峰值可能出現在前方的位置9或后方的位置7。

表4所示為在200 km/h撞擊速度下不同撞擊角度管片襯砌的拉壓損傷平均值、最大值及其對應的損傷面積。由表4可見：隨著斜向撞擊角度的增大，管片襯砌的拉壓損傷平均值、最大值及其對應的損傷面積都不斷增大。從總體上看，受拉損傷平均值及其最大值均大于受壓損傷平均值和最大值，受拉損傷平均值及其最大值在撞擊角度達到7.5°后，繼續增大撞擊角度，其值分別在0.287 3~0.319 2，0.861 8~0.957 6之間變化，變化幅度不大，而受壓損傷平均值及其最大值隨撞擊角度的增大而增大。受拉損傷面積同樣隨撞擊角度的增大而增大，從5.0°對應的8.5 m2逐漸增大到17.5°對應的25.5 m2，而受壓損傷面積只從5.0°對應的8.5 m2小幅變化到17.5°對應的13.5 m2。

表4 不同撞擊角度下各參數值

4 結論

1) 列車撞擊荷載主要與列車行駛速度、斜向撞擊角度以及列車編組數有關，當列車編組超過5節時，編組數對撞擊荷載的影響逐漸減弱。列車撞擊力在撞擊瞬間急劇增大并達最大值，隨后急速減小并震蕩持續波動一定時間。當撞擊角度超過12.5°或列車速度超過200 km/h時，撞擊力曲線還會出現第2個峰值；撞擊荷載作用時間與列車撞擊速度和角度有關，但基本處于25~40 ms。

2) 管片襯砌的各位置的峰值應力、位移、速度和加速度隨著列車撞擊速度的增大而增大。受拉損傷平均值及其最大值均大于受壓損傷平均值和最大值。受拉損傷平均值和受拉損傷面積隨著撞擊速度的增大迅速上升到較高水平，之后緩慢增長，而受壓損傷平均值和受拉損傷面積則隨著撞擊速度的增大而逐漸 增長。

3) 管片襯砌的各位置的峰值應力、位移、速度和加速度隨著列車撞擊角度的增大而增大。在相同撞擊速度下，隨斜向撞擊角度的增大，管片襯砌的拉壓損傷平均值、最大值及其對應的損傷面積都不斷增大；受拉損傷平均值及其最大值均大于受壓損傷平均值和最大值，受拉損傷平均值及其最大值隨撞擊角度增大快速增大，之后緩慢變化，而受壓損傷平均值及其最大值隨撞擊角度無明顯急速上升過程，表現出漸進增大趨勢。

[1] Müller F. 輕軌車輛的制造[J]. 國外鐵道車輛, 2000, 37(5): 7?11. Müller F. Manufacture of light rail vehicles[J]. Foreign Rolling Stock, 2000, 37(5): 7?11.

[2] 田口真. 鐵道車輛抗沖撞結構的開發[J]. 國外鐵道車輛, 2003, 40(6): 23?27. TIAN Kouzhen. Development of crashworthy structure of rolling stock[J]. Foreign Rolling Stock, 2003, 40(6): 23?27.

[3] 姚松, 田紅旗. 車輛吸能部件的薄壁結構碰撞研究[J]. 中國鐵道科學, 2001, 22(2): 55?60. YAO Song, TIAN Hongqi. Crash research on thin-shelled structure as vehicle energy-absorbing components[J]. China Railway Science, 2001, 22(2): 55?60.

[4] 房加志, 劉金朝, 焦群英, 等. 鐵路客車結構大變形碰撞特性的仿真研究[J]. 中國農業大學學報, 2004, 9(4): 76?78. FANG Jiazhi, LIU Jinchao, JIAO Qunying, et al. Simulation of collision characteristics of train vehicle with large deformation[J]. Journal of China Agricultural University, 2004, 9(4): 76?78.

[5] 李兆霞. 一個綜合模糊裂紋和損失的混凝土應變軟化本構模型[J]. 固體力學學報, 1995, 16(1): 22?30. LI Zhaoxia. A viscoplastic model combined damage and smeared crack for softening of concrete[J]. Chinese Journal of Solid Mechanics, 1995, 16(1): 22?30.

[6] 寧建國, 商霖, 孫遠翔. 混凝土材料沖擊特性的研究[J]. 力學學報, 2006, 38(2): 199?208. NING Jianguo, SHANG Lin, SUN Yuanxiang. Investigation on impact behavior of concrete[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2): 199?208.

[7] Burlion N, Fabrice G, Gilles P C, et al. Compaction and tensile damage in concrete: Constitutive modeling and application to dynamics[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 183(3): 291?308.

[8] 張厚美, 過遲, 呂國梁. 盾構壓力隧洞雙層襯砌的力學模型研究[J]. 水利學報, 2001, 32(4): 28?33, ZHANG Houmei, GUO Chi, Lü Guoliang. Mechanical model for shield pressure tunnel with secondary linings[J]. Journal of Hydraulic Engineering, 2001, 32(4): 28?33.

[9] 張厚美, 連烈坤, 過遲. 盾構隧洞雙層襯砌接頭相互作用模型[J]. 巖石力學與工程學報, 2003, 22(1): 70?74. ZHANG Houmei, LIAN Liekun, GUO Chi. Joint interaction model for shield tunnel segment reinforced by secondary linings[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 70?74.

[10] 趙德安, 雷曉燕, Swoboda G. 單、雙層襯砌隧道的非線性有限元分析[J]. 中國公路學報, 2003, 16(1): 62?67. ZHAO Dean, LEI Xiaoyan, Swoboda G. Nonlinear FEM analysis for single and double lining tunnels[J]. China Journal of Highway and Transport, 2003, 16(1): 62?67.

[11] 晏啟祥, 程曦, 何川, 等. 水壓條件下盾構隧道雙層襯砌力學特性分析[J]. 鐵道工程學報, 2010, 144(9): 55?59. YAN Qixiang, CHENG Xi, HE Chuan, et al. Analysis of mechanical properties of double-layered lining of shield tunnel under water pressure[J]. Journal of Railway Engineering, 2010, 144(9): 55?59.

[12] 施成華, 楊偉超, 彭立敏, 等. 高速鐵路隧道列車風作用下接觸網安全性分析[J]. 中南大學學報(自然科學版), 2012, 43(9): 3652?3658.SHI Chenghua, YANG Weichao, PENG Limin, et al. Analysis of catenary’s safety under train wind action in high-speed railway tunnel[J]. Journal of Central South University (Science and Technology), 2012, 43(9): 3652?3658.

[13] 李麗. 基于ABAQUS的高速公路隧道地震動力響應研究[D]. 成都: 西南交通大學土木工程學院, 2009: 11?15. LI Li. Study on seismic dynamic response of expressway tunnel based on ABAQUS[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineerin g, 2009: 11?15.

[14] GB 50010—2002, 混凝土結構設計規范[S]. GB 50010—2002, Code for design of concrete structures[S].

[15] 王娜娜, 馬衛華. 自動車鉤的彈簧剛度和阻尼系數對列車縱向動力學的影響[J]. 內燃機車, 2010(9): 1?3. WANG Nana, MA Weihua. Influence of spring stiffness and damping coefficient of automatic coupler on the longitudinal dynamics of train[J]. Diesel Locomotives, 2010(9): 1?3.

(編輯 劉錦偉)

Dynamic response of segment structure of double lining shield tunnel under train impact load

YANQixiang1, LI Bin1, ZHANG Meng2, CHEN Cheng1

(1. Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China;2. China Railway Engineering Consulting Group Co. Ltd., Beijing 100020, China)

A three-dimensional numerical analysis model of the train formation was established to obtain the time-history curves of the train impact force under different train formations, impact velocities and oblique impact angles. Based on HHT time integration scheme and concrete plastic damage model, the dynamic responses of the double lining shield tunnel caused by the impact force under different impact velocities and impact angles were studied, such as stress, displacement, velocity, acceleration, tension & compression damage factor and damaged area of the segment lining. The results show that the impact force is mainly related to the train impact velocity, oblique impact angle and train formation, and the time-history curve of the impact force has a second peak interval under certain conditions. Dynamic response increases with the increase of the impact velocity and impact angle, and the average and maximum value of tensile damage are higher than those of compressive damage, respectively. The relationship between tension & compression damage, the impact velocity and angle are obtained.

double lining; train impact load; segment lining structure; dynamic response; tension and compression damage

10.11817/j.issn.1672-7207.2015.09.049

U451.4

A

1672?7207(2015)09?3527?08

2014?09?02；

2014?11?23

國家自然科學基金資助項目(51178400，51278425，U1134208)；教育部新世紀人才支持計劃項目(NCET-11-0713) (Projects(51178400, 51278425, U1134208) supported by the National Natural Science Foundation of China; Project(NCET-11-0713) supported by the New Century Talents Project Funded by the Ministry of Education)

晏啟祥，博士，教授，博士生導師，從事隧道工程的教學與研究；E-mail: 764365015@qq.com