基于RBF-ARX模型的改進多變量預測控制及應用

曾小勇，彭輝，吳軍

?

基于RBF-ARX模型的改進多變量預測控制及應用

曾小勇1, 2，彭輝1，吳軍1

(1. 中南大學信息科學與工程學院，湖南長沙，410083；2. 長沙理工大學電氣與信息工程學院，湖南長沙，410076)

針對一類工作點時變的光滑非線性多變量被控對象，采用離線辨識的RBF-ARX模型描述系統的全局非線性動態特性，并在此基礎上提出一種具有自適應微分作用的非線性模型預測控制方法。該方法將整個預測時域內模型輸出和期望輸出的偏差變化率考慮到優化目標中，利用與偏差變化率有關的函數動態修改該優化項的權重,從而能在保證控制器穩態性能的情況下有效地改善系統的動態性能。最后利用該方法對四旋翼飛行器實驗裝置進行了實際的姿態控制，控制效果驗證該方法的有效性。

RBF-ARX模型；非線性模型預測控制；四旋翼飛行器

非線性模型預測控制(NMPC)由于突破了傳統控制策略的束縛，能有效處理工業過程中普遍存在的非線性現象和系統約束，而受到控制工程界和理論界的廣泛關注[1?2]。NMPC是一種基于預測模型的優化控制算法，對于工業過程中存在的各類非線性對象，采用線性化建模方法[3?4]難以完整描述工業現場大量存在的強非線性特性；而直接非線性建模[5?8]通常都包含有高階的在線非線性優化問題，對于實時性要求較高的實際工業對象很難取得滿意的控制效果。因此，近年來大量的研究和應用都側重于利用組合預測模 型[9?14]。該類方法將被控對象分解為非線性和線性空間，使整個系統具有局部線性全局非線性的特性，便于實現離線設計，在線綜合的預測控制算法，可大幅降低在線計算量，有利于在實際工業現場的應用。PID控制器由于其簡單的反饋控制結構仍廣泛應用于工業現場中，將PID控制思想與預測控制算法相結合可進一步提高預測控制器的性能。文獻[15?16]提出了一種比例積分型一步預測控制方法，并通過算例仿真結果說明了該方法的優越性，但由于未涉及到對象的建模，忽略了建模誤差對預測控制結果的影響，這在實際工業控制中將影響控制器的性能。本文作者針對一類工作點時變的光滑非線性多變量被控對象，采用狀態相依自回歸(SD-ARX)模型描述系統的非線性狀態特征，用高斯徑向基函數(RBF)神經網絡近似SD-ARX模型的函數型系數，在遞推得出以狀態信號量引導的多步狀態空間預測模型的基礎上，結合傳統的多步模型預測控制策略，將整個預測時域內模型輸出和期望輸出的偏差變化率考慮到優化目標中，相當于對偏差的微分也進行優化控制。為了減少建模誤差對控制器穩態誤差的影響，在優化過程中根據偏差變化率的信息動態調整其權重系數，從而能在保證控制器穩態性能不變的情況下有效地抑制由于系統慣性和輸入時滯所帶來的超調，縮短調節時間，改善系統的動態性能。最后，利用該方法對四輸入三輸出的四旋翼飛行器實驗裝置的飛行姿態進行實際控制，控制結果驗證了該方法的有效性。

1 非線性對象模型

1.1 非線性對象描述

對于工業過程中大量存在的非線性現象，建模的主要問題就是構建如下一個函數：

其中：()為輸出；()為輸入；a和b分別為輸出輸入階次；()為白噪聲序列。

其中：和=dim((?1))分別為RBF網絡的節點數和中心維數；和為RBF網絡描述的狀態相依ARX模型函數系數；和分別為RBF網絡的中心和寬度；，和，分別為RBF網絡的閥值和線性權重；為向量的2范數；為白噪聲序列。利用Peng等[17]提出的結構化非線性參數優化方法(SNPOM)離線估計模型參數。在實時控制中，模型(3)通過狀態信號量的更新來實時反映被控對象的動態特性。狀態信號量通常是選取最能反映被控對象動態特性的動態變量，所以它可能是與輸入或輸出有直接或間接的關系，在某些時候也可能就是輸入與輸出的組合或是其他相關信號量。當該狀態量為固定值時，狀態相依ARX模型就可以衍變成為一個ARX模型，因為系統狀態信號量的變化，狀態相依ARX模型能隨時在不同的局部子空間內進行即時平滑的轉換，從而使得狀態相依ARX模型具有全局有效的特性。

1.2 狀態相依ARX模型的狀態空間描述

將模型(3)變換成如下矩陣多項式形式：

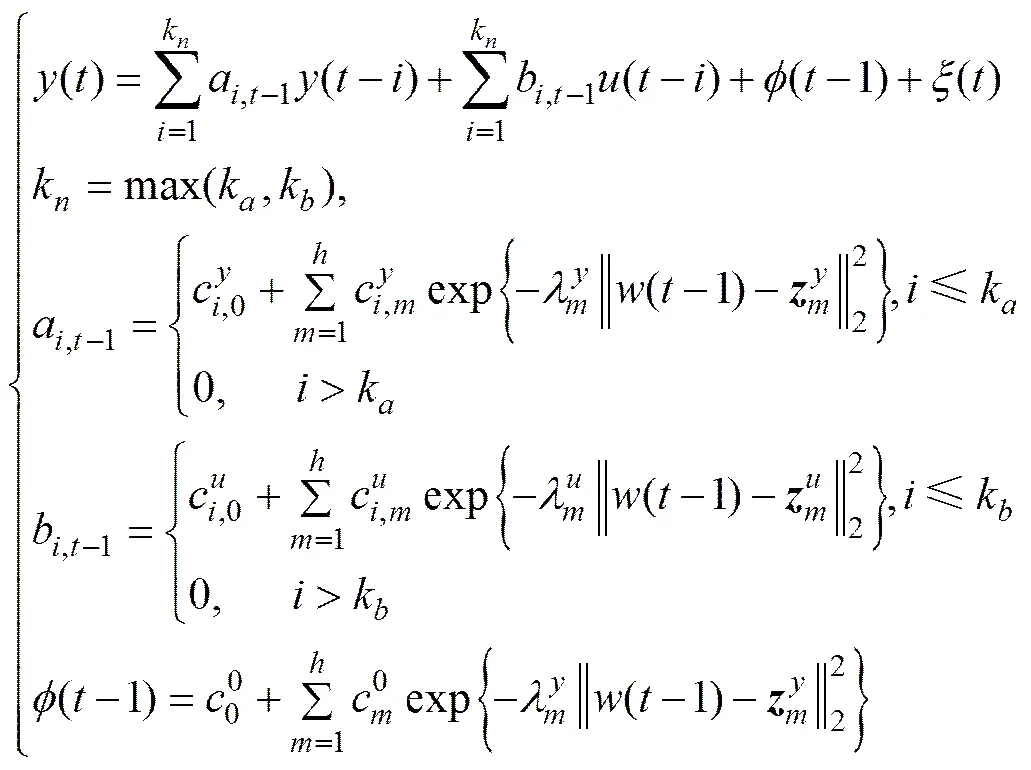
由此可根據模型(4)可定義如下的狀態變量：

(5)

根據模型(3)或模型(4)和定義的狀態變量式(5)可推出對象的狀態空間模型為

其中：

特別指出的是，通過狀態變量式(5)的定義，當前時刻的狀態()可以由過去時刻的狀態、輸入輸出數據以及估計的狀態相依ARX模型的系數計算得到，不需要再使用狀態觀測器估計當前時刻的狀態。

1.3 遞推多步狀態空間預測模型

模型(3)，(4)和(6)可認為是一步預測模型，為了得到非線性對象的多步預測模型，定義如下向量：

式中：和N分別為預測時域和控制時域，且滿足≥N，從N到時域內認為輸入為N時刻的輸入并保持不變；和()分別為時刻帶模型預測輸出序列和期望輸出序列，通常，期望輸出序列即參考軌跡為當前時刻期望值()的柔化序列：

定義系統的多步預測模型的狀態空間描述為

式中：

(13)

2 改進的非線性模型預測控制

傳統的非線性模型預測控制策略一般將非線性預測模型作為控制器的內模，將當前時刻的最優輸入問題轉化為某個有限預測時域內模型輸出和期望輸出的偏差最小的優化問題，同時根據模型輸出和實際輸出的歷史偏差信息對預測模型進行反饋校正，并在下一個采樣周期向前滾動優化。通常將模型預測控制的目標函數定義為

(17)

其中：，1和2為權重對角陣；()和分別為時刻優化的控制序列和控制增量序列。設置控制加權陣1和2是為了減少對被控對象過大的沖擊，一般情況下，加大其權重可以提高系統的穩定性，但同時也減弱了控制作用，還可能增大系統的穩態誤差，一般的做法是在系統能夠穩定的情況下，應使其權重盡可能的小。

優化控制的目的是為了找到一個控制量使得被控對象的性能滿足要求，調節式(17)中的權重系數和輸出期望序列()可均衡控制系統的動態和穩態性能，也就是說，某個較好的控制性能指標通常是以犧牲其他性能指標為代價的。特別對于一些復雜的實際工業對象，如何在保證控制器穩態性能不變的情況下有效地抑制由于系統慣性和輸入時滯所帶來的超調，縮短調節時間，改善系統的動態性能顯得尤為重要。根據PID的控制思想，輸出偏差微分項的引入可有效改善系統的動態性能。由此，改進型模型預測控制的目標函數定義為

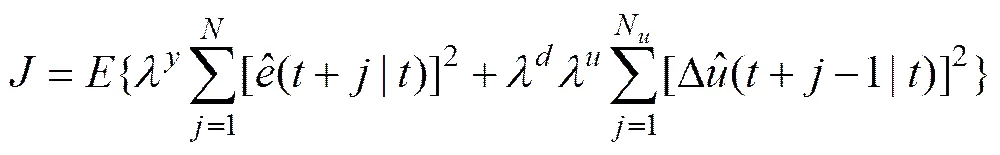
定義當前時刻模型預測輸出序列和期望輸出序列的偏差序列為

將式(21)變形為

可得到改進型的非線性模型預測控制目標函數為

(23)

式中：為偏差變化率的權重對角陣。

需要特別說明的是：

2) 由式(23)可以看出：優化的目標是期望獲得一組()使得()和，之間的偏差最小，在系統的動態過程中，可理解為對期望序列的在線修正，以幫助系統提前動作，減少系統的超調量，縮短調節時間。

3) 在系統進入穩態后，如果預測模型能準確地描述系統，即對象實際輸出等同于模型預測輸出，系統不存在穩態偏差，即在系統進入穩態后，，式(23)等同式(17)，可見，輸出偏差變化率的引入在改善系統的動態性能的同時不會影響系統的穩態性能。但由于實際系統的復雜，不可避免的存在模型失配，使得系統存在穩態偏差，此時輸出偏差變化率的引入可能導致穩態偏差的加大，為了消除偏差變化率對穩態偏差的影響，可將其權重系數定義為模型預測輸出序列和期望輸出序列的偏差變化率的函數。在動態過程中，是與系統動態特性相關的常數，此時偏差變化率權重較大，可有效改善系統的動態性能，當系統進入穩態后，將趨向于0，偏差變化率權重也將趨向于0，從而保證偏差變化率的引入在改善系統動態性能后不影響系統的穩態偏差。

將式(10)進行如下變換，

則可將式(23)轉化為標準的二次規劃形式：

(25)

其中：

是和輸入變量數有關的常數項矩陣。

式(25)的求解是一個非線性在線優化問題，可通過二次規劃相關方法進行優化，當不考慮式(25)的約束條件時，可直接對輸入進行求導限幅，求得輸入序列為

對于優化得到的輸入序列，僅使用最新時刻的輸入作為控制輸入。

3 應用研究

3.1 對象描述

圖1所示為四旋翼飛行器物理結構圖。為了驗證本文方法的有效性和可行性，選取實驗室基于物理模型的二次型最優調節器(LQR)控制的四旋翼飛行器姿態控制實驗裝置(如圖１所示)為被控對象，四旋翼飛行器是一個四輸入三輸出的非線性帶耦合對象，4個輸入分別是對4個螺旋槳提供動力的電機電壓，約束為[?20 V，20 V]，3個輸出分別為繞軸旋轉的俯仰角、繞軸旋轉的翻轉角和繞軸旋轉的巡航角。

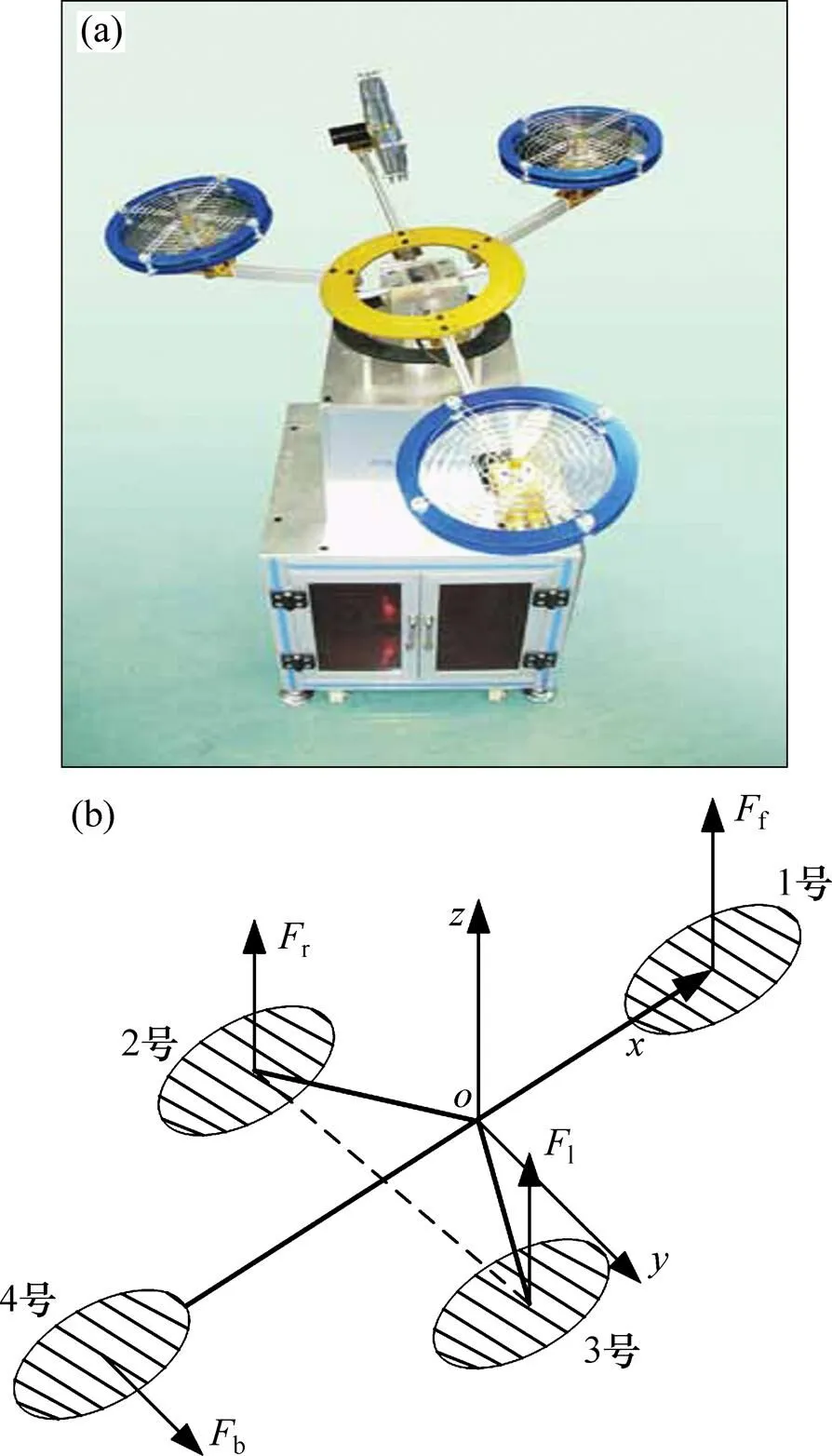
(a) 實物圖；(b) 力學坐標圖

3.2 對象模型

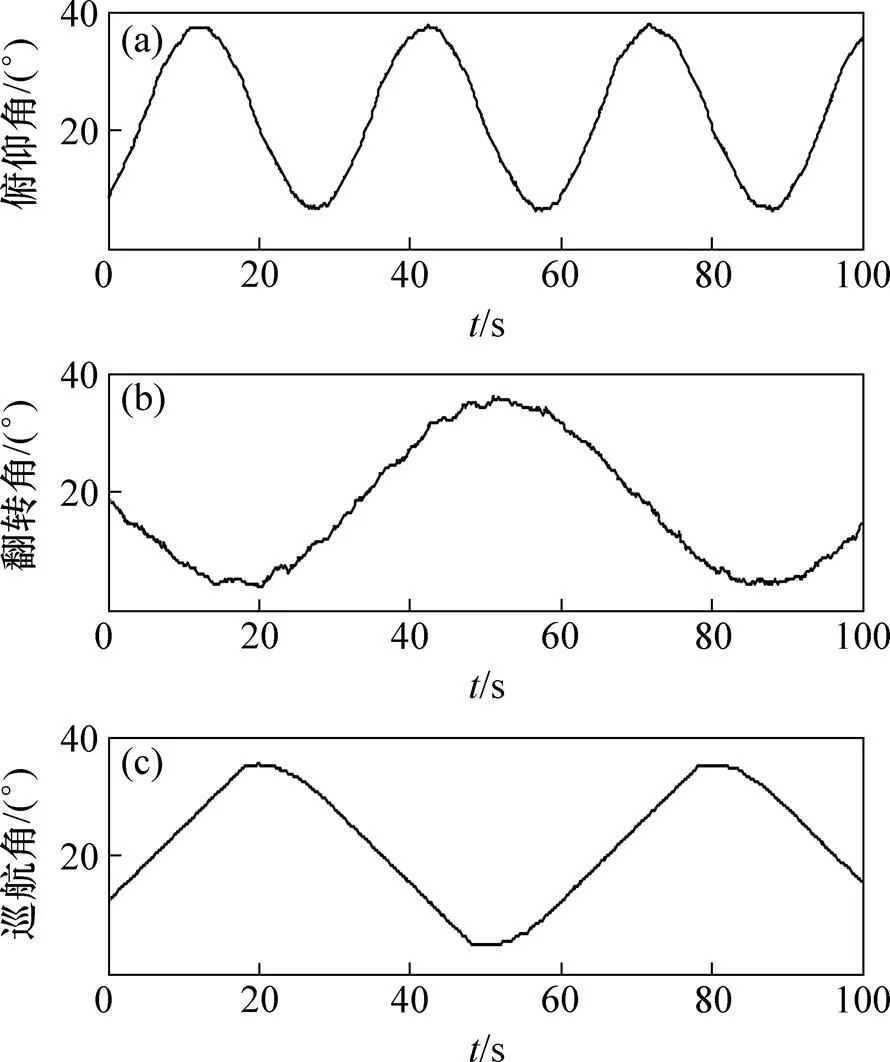
(a) 俯仰角；(b) 翻轉角；(c) 巡航角

(a) 俯仰角；(b) 翻轉角；(c) 巡航角

從圖2和3可以看出：狀態相依ARX模型具有較好的建模效果，模型預測輸出很好的擬合了實際輸出，預測誤差近似白噪聲信號且總體在很小的范圍內變動。

3.3 實時控制效果及分析

確定預測時域=30，控制時域N=10，柔化因子=0.1，線性權重對角陣為，且在每個預測時域內保持不變。為了驗證改進型非線性模型預測控制方法的改進效果，在保持其他參數不變的情況下，將模型預測輸出序列和期望輸出序列的偏差變化率考慮到優化目標中，為了保證偏差變化率的引入在改善系統的動態性能的同時不影響穩態性能，式(18)中權重對角陣的動態調整非常關鍵，本文將其取為關于第1個預測時域的偏差變化率的函數，(式中：分別為3個輸出偏差變化率絕對值的均值)。

圖4所示為傳統非線性模型預測控制(實線)和改進型非線性模型預測控制(點線)的階躍響應曲線。由于四旋翼飛行器狀態是飛行器的水平狀態，這一狀態是十分敏感的，小幅的波動都將使其從這一狀態滑落，這一狀態的改變最能體現控制器的控制效果。由圖4可知：改進的方法在減少系統超調和縮短調節時間的同時沒有增加系統的穩態偏差。另外由于飛行器的巡航角具有較大的偏差變化率加權，使得其上升緩慢，但動態性能也優于傳統非線性模型預測控制器。

(a) 俯仰角；(b) 翻轉角；(c) 巡航角

圖5所示為改進型非線性模型預測控制階躍響應對應的輸入曲線，4個輸入都很好地約束在[?20 V，20 V]內。圖6所示為用于動態調整偏差變化率加權的第1個預測時域內的模型輸出和期望輸出偏差變化率曲線。由圖6可知：當系統處于動態變化過程時，偏差變化率較大，而當系統過渡到穩態時，偏差變化率趨向于0，從而保證了偏差變化率的引入在改善系統動態特性的同時不影響系統的穩態性能。

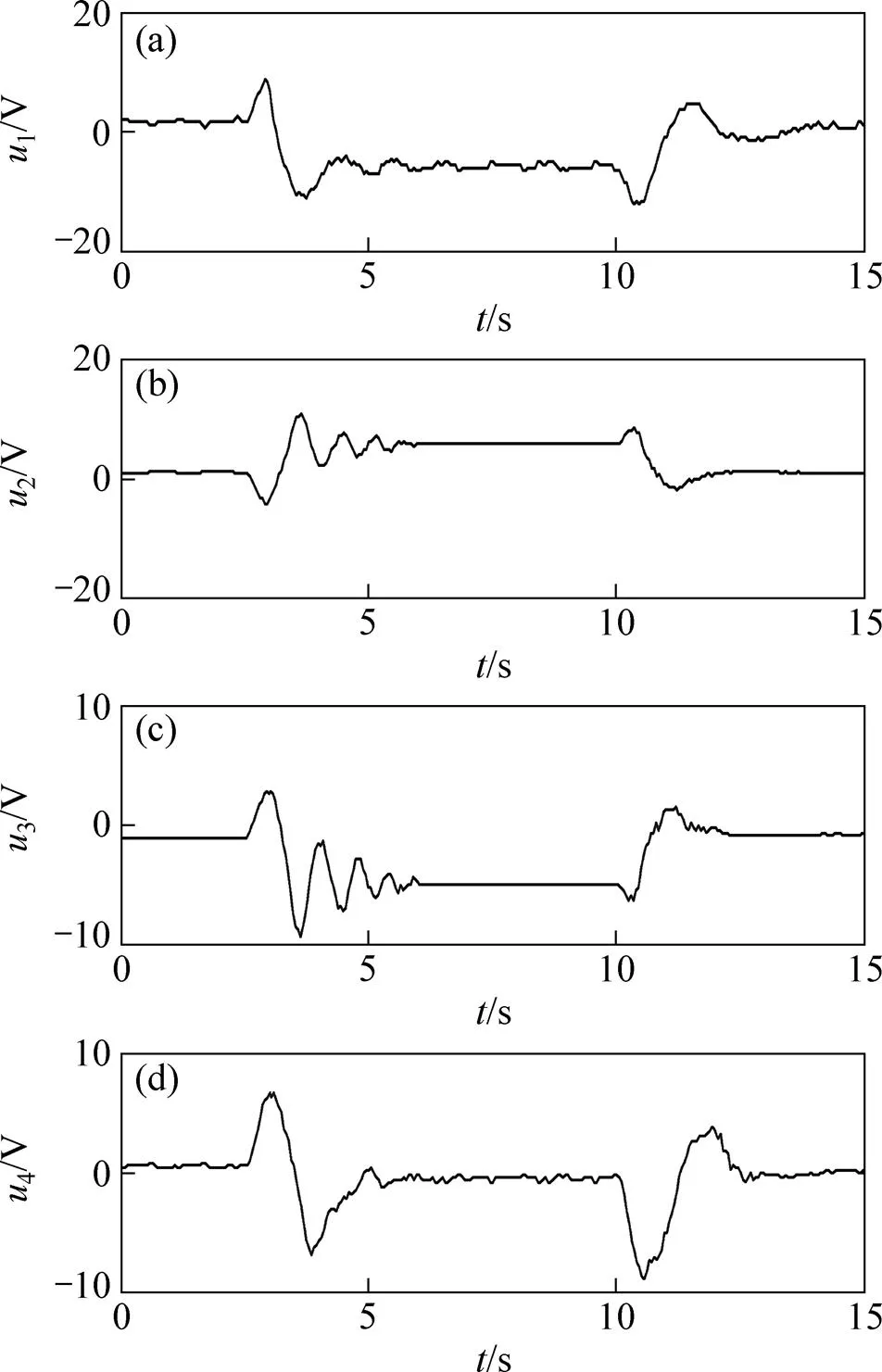
(a) Vf；(b) Vr；(c) Vl；(d) Vb

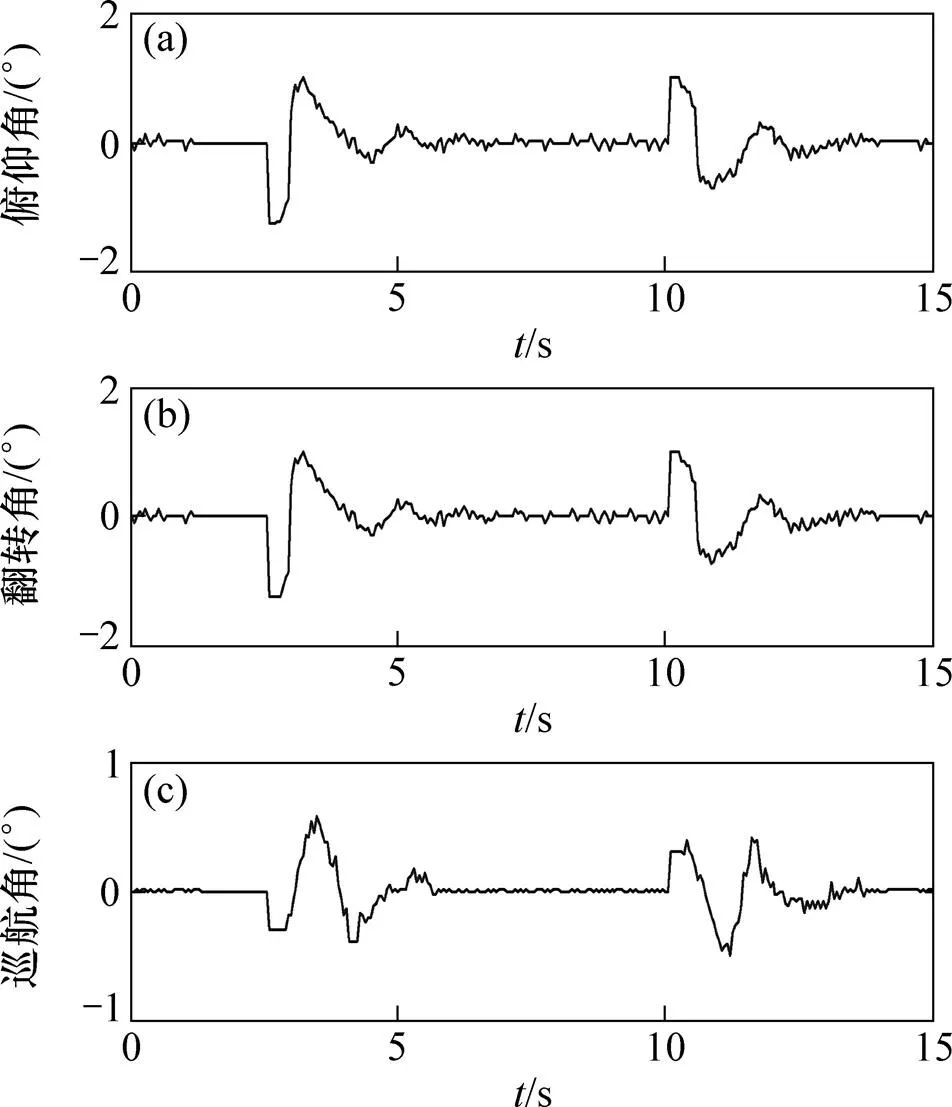
(a) 俯仰角；(b) 翻轉角；(c) 巡航角

由于本文采用離線的結構化非線性參數優化方法估計模型參數，采用Ｃ語言編制程序，并在算法上盡量進行了簡化，使得復雜的非線性預測控制策略得以在50 ms的控制周期內實現。

4 結論

對一類工作點時變的多變量非線性系統提出了一種改進型的非線性模型預測控制方法，該方法將模型預測輸出和期望輸出的偏差變化率引入到滾動優化中，同時利用與偏差變化率有關的函數動態修改該優化項的權重，使得該方法在保證系統穩態性能的情況下有效改善系統的動態性能，利用該方法對四旋翼飛行器實驗裝置進行實時控制，取得了比傳統的非線性模型預測控制算法更好的控制效果。

[1] 席裕庚, 李德偉. 預測控制定性綜合理論的基本思路和研究現狀[J]. 自動化學報, 2008, 34(10): 1225?1234. XI Yugeng, LI Dewei. Fundamental philosophy and status of qualitative synthesis of model predictive control[J]. Acta Automatica Sinica, 2008, 34(10): 1225?1234.

[2] Qin S J, Badgwell T A. A survey of industrial model predictive control technology[J]. Control Engineering Practice, 2003, 5(11): 733?764.

[3] Prasad G, Swidenbank E, Hogg B W. A local model networks based multivariable long-rang predictive control strategy for thermal power plants[J]. Automatica, 1998, 34(2): 1185?1204.

[4] Giarre L, Bauso D, Falugi P, et al. LPV model identification for gain scheduling control: An application to rotating stall and surge control problem[J]. Control Engineering Practice, 2006, 14(4): 351?361.

[5] Mizuno N, Kuroda M, Okazaki T. Minimum time ship maneuvering method using neural network and nonlinear model predictive compensator[J]. Control Engineering Practice, 2007, 9(12): 1353?1360.

[6] ZHANG Haitao, LI Hanxiong, CHEN Guanrong. Dual-mode predictive control algorithm for constrained Hammerstein systems[J]. International Journal of Control, 2008, 81(10): 1609?1625.

[7] Arefi M M, Montazeria A, Poshtana J, et al. Wiener neural identification and predictive control of a more realistic plug flow tubular reactor[J]. Chemical Engineering Journal, 2007, 138(1/2/3): 274?282.

[8] Piche S, Sayyar-Rodsari B, Johnson D, et al. Nonlinear model predictive control using neural networks[J]. IEEE Control Systems Magazine, 2000, 20(3): 53?62.

[9] 李妍, 毛志忠. 基于多面體終端域的Hammerstein-Wiener非線性預測控制[J]. 自動化學報, 2011, 37(5): 629?638. LI Yan, MAO Zhizhong. Predictive control of Hammerstein- Wiener nonlinearity based on poly-topic terminal region[J]. Acta Automatica Sinica, 2011, 37(5): 629?638.

[10] Cervantes A L, Agamennoni O E, Figueroa J L.A nonlinear model predictive control system based on Wiener piece wise linear models[J]. Journal of Process Control, 2003, 13(7): 655?666.

[11] 師五喜. 未知多變量非線性系統自適應模糊預測控制[J]. 控制理論與應用, 2011, 28(1): 1399?1405. SHI Wuxi. Adaptive fuzzy predictive control for unknown multivariable nonlinear systems[J]. Control Theory & Applications, 2011, 28(1): 1399?1405.

[12] Peng H, Nakano K, Shioya H. Nonlinear predictive control using neural nets-based local linearization ARX model-stability and industrial application[J]. IEEE Transaction on Control Systems Technology, 2007, 15(1): 130?143.

[13] Peng H, Kitagawa G, Wu J, et al. Multivariable RBF-ARX model-based robust MPC approach and application to thermal power plant[J]. Applied Mathematical Modeling, 2011, 35(7): 3541?3551.

[14] Wu J, Peng H, Ohtsu K, et al. Ship’s tracking control based on nonlinear time series model[J]. Applied Ocean Research, 2012, 36(6): 1?11.

[15] ZHANG Yan, CHEN Zengqiang, YUAN Zhuzhi. Nonlinear system PID-type multi-step predictive control[J]. Journal of Control Theory and Applications, 2004, 2(2): 201?204.

[16] 李韜, 陳增強, 張紀峰. 比例積分型廣義預測控制系統的穩定性分析[J] 控制理論與應用, 2007, 24(1): 19?25. LI Tao, CHEN Zengqiang, ZHANG Jifeng. Stability analysis of systems with proportional-integral generalized predictive control[J]. Control Theory & Applications, 2007, 24(1): 19?25.

[17] Peng H, Ozaki T, Haggan-Ozaki V, et al. A parameter optimization method for radial basis function type models[J]. IEEE Transaction on Neural Networks, 2003, 14(2): 432?438.

An improved multivariable RBF-ARX model-based nonlinear model predictive control approach and application

ZENG Xiaoyong1, 2, PENG Hui1, WU Jun1

(1. School of Information Science and Engineering, Central South University, Changsha 410083, China; 2. School of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410076, China)

For a class of smooth nonlinear multivariable systems whose working-points vary with time, a Gaussian radial basis function (RBF) neural networks-based local linearization autoregressive with exogenous (ARX) model was built to describe the system’s global behavior, and an improved nonlinear model predictive control (NMPC) method with adaptive differential effect based on RBF-ARX model identified offline was presented. Difference from conventional NMPC, the differential of errors between model outputs and designed outputs in whole prediction horizon were considered and their weights were adapted by functions of themselves in each optimization process, thus the controller can improve dynamic performance when the steady-state performance is ensured. A case study on a quadrotor for its real attitude control indicates that the proposed method is effective.

RBF-ARX model; nonlinear model predictive control; quadrotor

10.11817/j.issn.1672-7207.2015.10.022

TP 273

A

1672?7207(2015)10?3710?08

2015?03?10；

2015?06?19

國家自然科學基金資助項目(71271215，71221061)；國家國際科技合作計劃項目(2011DFA10440)；湖南省教育廳項目(12C0021)(Projects (71271215, 71221061) supported by the National Natural Science Foundation of China; Project (2011DFA10440) supported by the International Science & Technology Cooperation Program of China; Project (12C0021) supported by the Hunan Provincial Education Department)

彭輝，教授，博士生導師，從事復雜非線性系統的建模與優化控制；E-mail：huipeng@csu.edu.cn

(編輯 陳愛華)