兩個Gamma商函數的對數完全單調性

劉媛，王連堂

（西北大學數學學院，陜西 西安　710127）

兩個Gamma商函數的對數完全單調性

劉媛，王連堂

（西北大學數學學院，陜西 西安710127）

主要研究了Gamma商函數的對數完全單調性.通過引入一個新的輔助函數證明了一類Gamma商函數是嚴格對數完全單調的，對此類函數的系數進行了推廣并證明了推廣后的這類Gamma商函數也是嚴格對數完全單調的.

Gamma函數；Psi（digamma）函數；Polygamma函數；對數完全單調性

1　引言

Gamma函數定義為：

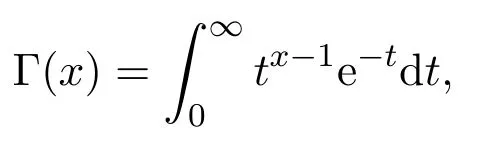
lnΓ（x）的導函數稱為psi函數（digamma函數）記為ψ（x），即

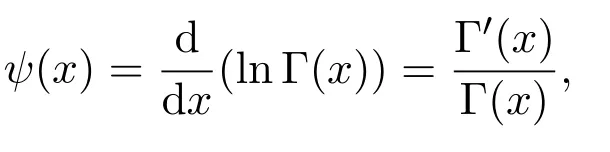
ψ（x）的n階導函數ψ（n）（x）稱為polygamma函數.

所謂Gamma商函數是指關于某些Gamma函數的商，關于Gamma商函數的完全單調性的研究是非常有意義的課題.文獻［1］證明了函數在區間（0，+∞）上為嚴格對數凹的.文獻［2］推廣了這一結果，證明了G（x）的倒數函數G-1（x）在區間（0，+∞）上是嚴格對數完全單調的.文獻［3］證明了函數在區間（0，+∞）上是對數完全單調的，其中m≥2是整數.

對數完全單調概念的提出，為研究函數的完全單調性提供了簡便的方法.本文通過引入一個新的輔助函數證明了當m為大于1的正實數時，F（x）是嚴格對數完全單調的，從而推廣了文獻［3］中的結果.另外，也證明了關于F（x）的一個推廣的函數（即定理3.2中的h（x））是嚴格對數完全單調的.

2　定義及引理

定義 2.1［4］函數f在區間I上稱為是完全單調的，若函數f在區間I上有任意階導數，并且對于任意x∈I以及n=0，1，2，···，滿足（-1）nf（n）（x）≥0；若此不等式是嚴格的，則稱f是嚴格完全單調的.

定義 2.2［5］正函數 f在區間 I上稱為是對數完全單調的，若對于任意 x∈I以及n=0，1，2，···，滿足（-1）n［lnf（x）］（n）≥0；若此不等式是嚴格的，則稱f是嚴格對數完全單調的.

文獻［5］中證明了（嚴格）對數完全單調函數一定是（嚴格）完全單調的.

引理2.1［6］當x∈（0，+∞）時，有

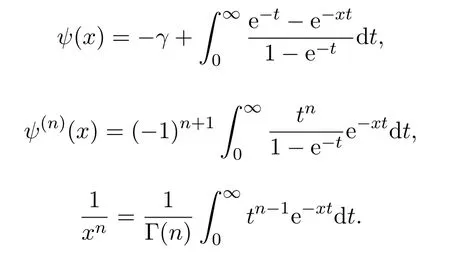
引理 2.2［6］函數 f（x）在區間 （0，+∞）上完全單調的充要條件是存在單調遞增的函數α（t），使得f（x）=∫∞0e-xtdα（t）.

引理 2.3［7］（Laplace變換的卷積定理）設函數fi（t）（i=1，2）在任意有限區間上是分段連續的，包括（0，+∞）.如果存在常數Mi＞0和ci≥0，有|fi（t）|≤Miecit（i=1，2），那么

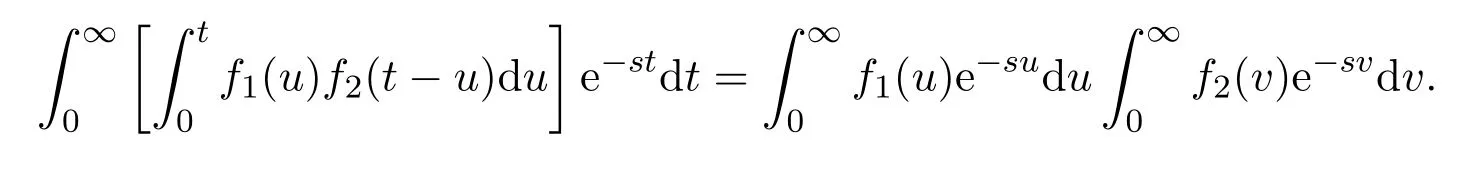
3　主要定理及其證明

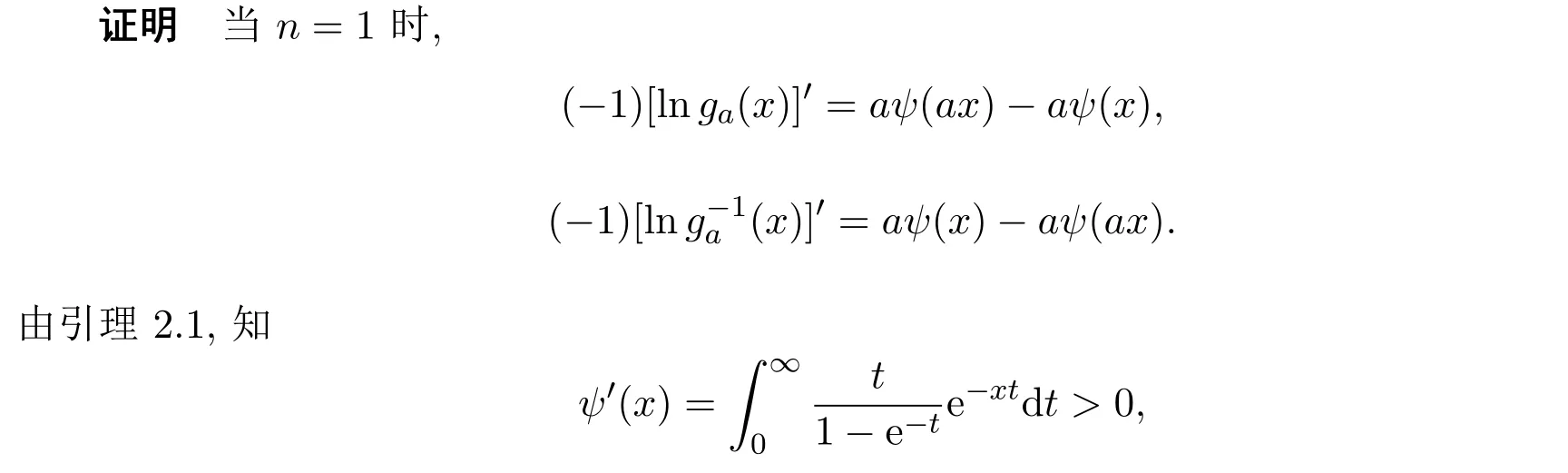
4　小結

文章通過引入一個新的輔助函數（即定理證明中的?（x））證明了兩類Gamma商函數的嚴格對數完全單調性，這推廣了文獻［3］中的結果，并且此種證明方法更加簡單直接.

［1］Merkle M.On log-convexity of a ratio of gamma functions［J］.Univ.Beograd.Publ.Elektrotehn.Fak.Ser.Mat.，1997，8：114-119.

［2］Chen Chaoping.Complete monotonicity properties for a ratio of gamma functions［J］.Univ.Beograd.Publ.Elektrotehn.Fak.Ser.Mat.，2005，16：26-28.

［3］Li Aijun，Chen Chaoping.Logarithmically complete monotonicity and Shur-convexity for some ratios of gamma functions［J］.Univ.Beograd.Publ.Elektrotehn.Fak.Ser.Mat.，2006，17：88-92.

［4］Qi Feng，Guo Senlin.Complete monotonicities of functions involving the gamma and digamma functions［J］.Applied Mathematics and Computation，2004，7（1）：63-72.

［5］Qi Feng，Chen Chaoping.A complete monotonicity property of the gamma function［J］.Journal of Mathematical Analysis and Applications，2004，296（2）：603-607.

［6］Chen Chaoping，Qi Feng.Logarithmically completely monotonic functions relating to the gamma function［J］.Journal of Mathematical Analysis and Applications，2006，321（1）：405-411.

［7］Guo Senlin，Qi Feng，Srivastava H M.A class of logarithmically completely monotonic functions related to the gamma function with applications［J］.Integral Transforms and Special Functions，2012，23（8）：557-566.

［8］Necdet Batir.On some properties of digamma and polygamma functions［J］.Journal of Mathematical Analysis and Applications，2007，328（1）：452-465.

［9］Qi Feng，Christian Berg.Complete monotonicity of a difference between the exponential and trigamma functions and properties related to a modified bessel functions［J］.Mediterranean Journal of Mathematics，2013，10（4）：1685-1696.

［10］王竹溪，郭敦仁.特殊函數概論［M］.北京：北京大學出版社，2000.

Logarithmically complete monotonicity of two classes of functions for the ratio of Gamma function

Liu Yuan，Wang Liantang

（College of Mathematics，Northwest University，Xi′an710127，China）

In this article，logarithmically complete monotonicity for the ratio of gamma functions is presented.By introducing a new function，we prove that the ratio of gamma function is strictly logarithmically completely monotonic.We also prove that a generalized form of the function is strictly logarithmically completely monotonic.

Gamma function，Psi（digamma）function，Polygamma function，logarithmically complete monotonicity

O174.6

A

1008-5513（2015）03-0291-05

10.3969/j.issn.1008-5513.2015.03.010

2014-12-03.

陜西省自然科學基金（2010JM1017）.

劉媛（1990-），碩士生，研究方向：特殊函數論.

2010 MSC：26A48