巴拿赫代數上序錐度量空間中的不動點定理
李改葉,薛西鋒
(西北大學數學學院,陜西 西安 710127)
巴拿赫代數上序錐度量空間中的不動點定理
李改葉,薛西鋒
(西北大學數學學院,陜西 西安710127)
提出了巴拿赫代數上的錐度量空間的相關概念,并給出了巴拿赫代數上元素的譜半徑的一些性質,證明了巴拿赫代數上錐度量空間中偏序集上的一些不動點定理,所得結論推廣了已知結果.
巴拿赫代數;錐度量空間;不動點定理;偏序集
1 引言
文獻[1]提出了巴拿赫代數上錐度量空間的概念,并得到了廣義利譜希茨映射條件下的不動點定理.文獻[2]提出了巴拿赫代數上錐度量空間中在沒有正規性的條件下廣義利譜希茨映射的不動點定理,文獻[3]研究了錐度量空間中偏序集上的不動點定理.本文在文獻[1-3]的基礎上,證明了巴拿赫代數上錐度量空間中偏序集上的一些不動點定理的存在性,從而推廣了文獻[1-3]的主要結果.
本文假設巴拿赫代數A有單位元e,即?x∈A,ex=xe=x.如果?x∈A,存在y∈A使得xy=yx=e,則x可逆,即y=x-1.本文用θ表示巴拿赫代數上的零元.
定義1.1[1]設A為巴拿赫代數,P為A中的非空子集,如果P滿足:
(i){θ,e}?P;
(ii)?α,β∈R且α,β≥0,αP+βP?P;
(iii)P2=PP?P;
(iv)P∩(-P)={θ},
則稱P是A中的錐.A中偏序是由P導出的.
定義1.2[1]設X為非空子集,A為巴拿赫代數,假定映射d:X×X→A滿足:
(i)?x,y∈X,d(x,y)≥θ且d(x,y)=θ?x=y;
(ii)?x,y∈X,d(x,y)=d(y,x);
(iii)?x,y,z∈X,d(x,y)≤d(x,z)+d(z,x),
則稱d為X上的錐度量,稱(X,d)為巴拿赫代數上的錐度量空間.
引理1.1[2]A為具有單位元e的巴拿赫代數,P為A中的錐,A中半序“≤”由P導出.設k∈P,如果ρ(k)<1,則
(i)k<e,即e-k>θ且(e-k)-1>θ成立;
(ii)若對u∈A有u≤ku,則u=θ;
(iii)ρ((e-k)-1)≤(1-ρ(k))-1成立.
引理1.2[2]A為巴拿赫代數,x,y∈A,如果x和y交換,則下面結論成立:
(i)ρ(xy)≤ρ(x)ρ(y);
(ii)ρ(x+y)≤ρ(x)+ρ(y);
(iii)|ρ(x)-ρ(y)|≤ρ(x-y).
定義1.3[3-4]錐P是正規的,若存在常數N>0,使得θ≤x≤y?∥x∥≤N∥y∥,且稱滿足條件的最小正數N為P的正規常數.
定義1.4[5-7]設(X,d)為巴拿赫代數A上的錐度量空間,x∈X,{xn}為X中的序列,則
(i)若?θ?c,總存在自然數N,當n>N時,都有d(xn,x)?c,則稱{xn}收斂到x,記為

(ii)若?θ?c,總存在自然數N,當n>N時,都有d(xn,xm)?c,則稱{xn}為X中的Cauchy列;
(iii)若X中的每個Cauchy列都在X中是收斂的,則稱(X,d)是完備的.
2 主要結果及其證明
定理2.1設(X,?)為偏序集,(X,d)為巴拿赫代數A上的完備錐度量空間,且A有單位元e,P為帶有正規常數M的正規錐,設映射f:X→X是關于“?”的連續非減映射,滿足:
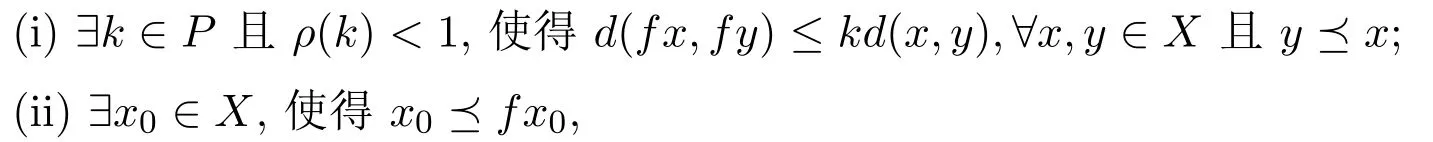
則f有不動點.


定理2.2設(X,?)為偏序集,(X,d)為巴拿赫代數A上的完備錐度量空間,且A有單位元e,設f:X→X是關于“?”的非減映射,滿足:

則f在X中有不動點.

推論2.1設(X,?)為偏序集,(X,d)為巴拿赫代數A上的完備錐度量空間,且A有單位元e,P為帶有正規常數M的正規錐,設f:X→X是關于“?”的非減映射,滿足:

則f在X中有不動點.
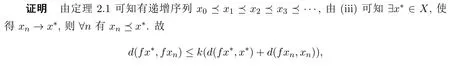

推論2.2設(X,?)為偏序集,(X,d)為巴拿赫代數A上的完備錐度量空間,且A有單位元e,設f:X→X是關于“?”的非減映射,滿足:
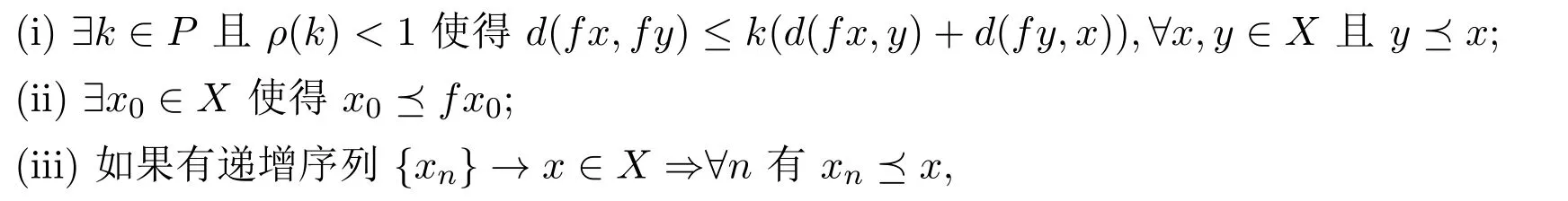
則f在X中有不動點.
證明同推論2.1的證明.
定理2.3設(X,?)為偏序集,(X,d)為巴拿赫代數A上的完備錐度量空間,且A有單位元e,P為帶有正規常數M 的正規錐,f:X→X是關于“?”的連續非減映射,滿足:
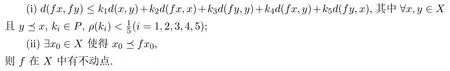


[1]Liu H,Xu S Y.Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings[J].Fixed Point Theory and Applications,2013,320:1-10.
[2]Xu S Y,Stojan R.Fixed point theorems of generalized Lipschitz mappings on cone metric spaces over Banach algebras without assumption of normality[J].Fixed Point Theory and Applications,2014,102:1-12.
[3]Altun I,Durmaz G.Some fixed point theorems on ordered cone metric spaces[J].Rendiconti del Circolo Matematico di palermo,2009,58(2):319-325.
[4]孫經先.非線性泛函分析及應用[M].北京:科學出版社,2007.
[5]Huang L G,Zhang X.Cone metric spaces and fixed point theorems of contractive mappings[J].Journal of Mathematical Analysis and Application,2007,332(2):1468-1476.
[6]Rudin W.Functional Analysis[M].2nd ed.New York:McGraw-Hill,1991.
[7]Liu H,Xu S.Fixed point theorem of quasicontractions on cone metric spaces with Banach algebras[J].Abstract and Applied Analysis,2013,DOI:10.1152/2013/187348.
Some fixed point theorems on ordered cone metric spaces with Banach algebras
Li Gaiye,Xue Xifeng
(College of Mathematics,Northwest University,Xi′an710127,China)
This paper presents the concept of cone metric spaces with Banach algebras and gives some properties of the spectral radius of the Banach algebra elements.Some fixed point theorem on ordered set in cone metric spaces with Banach algebra are proved,and the conclusions generalize known results.
Banach algebra,cone metric space,fixed point theorem,ordered set
O177.91
A
1008-5513(2015)03-0318-05
10.3969/j.issn.1008-5513.2015.03.013
2014-12-16.
陜西省自然科學基金(2012JM1017).
李改葉(1989-),碩士生,研究方向:非線性泛函分析.
2010 MSC:60B12

