向量優化問題C（ε）-真有效解的Kuhn-Tucker最優性條件

張萬里，趙克全

（重慶師范大學數學學院，重慶　401331）

向量優化問題C（ε）-真有效解的Kuhn-Tucker最優性條件

張萬里，趙克全

（重慶師范大學數學學院，重慶401331）

在實局部凸Hausdorff拓撲線性空間中基于co-radiant集提出了C（ε）-真有效性概念.用實例證明其與相關文獻中提出的真ε-有效性不同，且包含Benson真有效性作為其特例.此外，在鄰近C（ε）-次似凸性假設下獲得了Kuhn-Tucker型必要條件，利用標量化定理得到了Kuhn-Tucker型充分條件.

向量優化；C（ε）-真有效解；Kuhn-Tucker最優性條件

1　引言及預備知識

在向量優化問題研究中，真有效性概念起著十分重要的作用［1-2］.近年來，引起了國內外學者的廣泛關注，并取得了一系列重要的研究成果.1979年，文獻［3］提出了一類改進的真有效性—-Benson真有效性.2000年，文獻［4］利用Benson真有效性的思想，提出了ε-Benson真有效性，并建立了標量化定理、ε-Lagrange乘子定理、ε-真鞍點定理和ε-真對偶定理.2006年，文獻［5］引進了co-radiant集這類新的工具，提出了新的ε-有效性概念，推廣并且統一了很多現有的真有效性及近似真有效性概念.2011年，文獻［6］借助于Gutiérrez等人的思想引進了Benson意義下近似真有效解的概念并包含了Benson真有效解作為其特例，利用非線性標量化函數建立了最優性條件，并在錐次似凸假設下建立了線性標量化定理.2012年，文獻［7］提出了與文獻［6］等價的C（ε）-真有效解概念，并在鄰近錐次似凸假設下建立了標量化定理，獲得了近似真鞍點定理.其它類型的近似真有效解概念可參見文獻［8-9］等.

受文獻［6-8］的啟發，本文在實局部凸Hausdorff拓撲線性空間中基于co-radiant集提出了C（ε）-真有效性概念，它包含了Benson真有效性作為其特例.通過例子說明了C（ε）-真有效性概念與文獻［6］中提出的真ε-有效性概念不同.進一步在鄰近C（ε）-次似凸假設下，獲得了C（ε）-真有效解的Kuhn-Tucker型最優性必要條件，并利用標量化定理得到了C（ε）-真有效解的Kuhn-Tucker型最優性充分性條件.此外，給出了與向量優化問題等價的無約束優化.

假設X為拓撲線性空間，Y，Z為實局部凸Hausdorff拓撲線性空間，K和P分別表示Y 和Z中的閉凸點錐.若K∩（-K）=｛0｝，則稱K為點的.令C?Y、int C、cl C、cone C分別表示C的內部、閉包和錐包.稱C是真的，若?≠C≠Y.若αc∈C，?c∈C，?α＞1，則稱C為co-radiant集.稱C是星型集，如果存在q∈C使得

引理 1.1［5］設ε＞0，C?Y為真星型co-radiant集且int（kern C）≠?，則

引理1.2［10］設閉凸錐K1，K2?Y且K1∩K2=｛0｝.若K2是點錐且是局部緊的，則

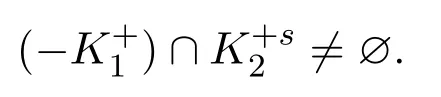
引理1.3［11］設V是實局部凸空間，凸集M，N?V滿足

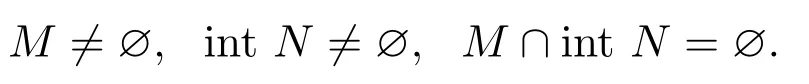
則存在V中的超平面分離M和N.

引理1.4［12］設A，B?Y，則A+int B?int（A+B）.

引理1.5［13］設A，B?Y，int A=A.若B是凸集且int B≠?，則A+B=A+int B.

2　C（ε）-真有效點的定義及性質

本節基于星型co-radiant集，提出C（ε）-真有效點的定義，通過具體例子說明它與文獻［6］中提出的真ε-有效點的概念不同，并包含Benson真有效點作為其特例.此外，還給出了關于C（ε）-真有效點性質的一個定理.

定義 2.1設ε≥0，C?Y為真星型co-radiant集且int（kern C）≠?，A?Y.若

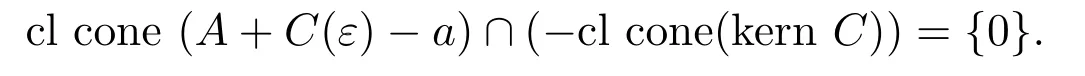
則稱a∈A是C（ε）-真有效點.C（ε）-真有效點的全體記為PE（A，C，ε）.

注2.1（i）當C?K，cl cone（kern C）=K時與文獻［7］中的定義是一致的；

（ii）當cl cone（kern C）=K時，PE（A，C，0）就退化為經典的Benson真有效性；

（iii）本文的定義與文獻［6］中的定義不等價，以下例子可以說明這一點.

例2.1令

例2.2令

定理2.1 （i）PE（A，C，0）?PE（A，C，ε），?ε＞0；

（ii）PE（A，C，ε1）?PE（A，C，ε2），?ε2＞ε1＞0；

（iii）若x∈PE（A，C，ε），則x∈PE（A，C，aε），?a＞1，?ε＞0；

證明根據定義2.1及C（ε）的性質，容易得到定理2.1的結論成立.

3　C（ε）-真有效解的Kuhn-Tucker最優性條件

向量優化問題在各種解意義下的最優性條件是最優化理論及應用的重要組成部分，是建立現代算法的重要基礎.下面給出C（ε）-真有效解的Kuhn-Tucker型最優性必要條件和充分條件.

本文考慮集值優化問題：

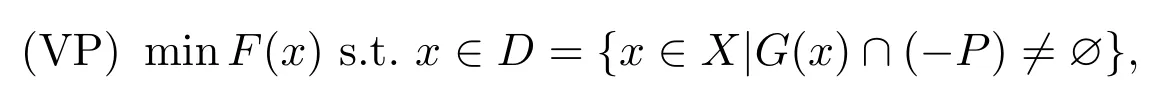
其中集值映射F：X?Y，G：X?Z具有非空值且D≠?.定義

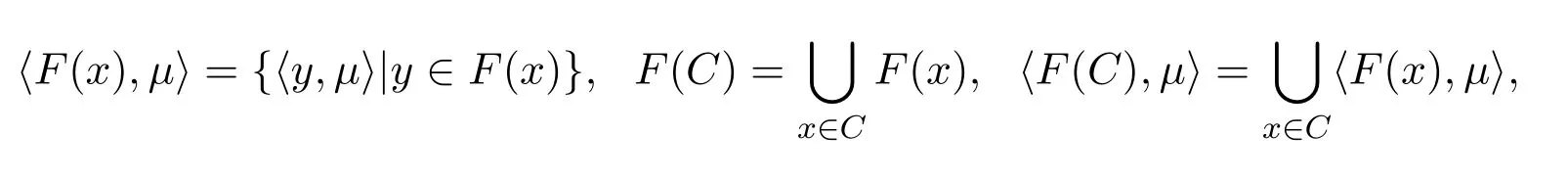
這里μ∈Y?，C?X.（F，G）表示從X到Y×Z的集值映射，記作（F，G）（x）=F（x）×G（x）.

設ε≥0，x0∈D稱為（VP）的C（ε）-真有效解，如果F（x0）∩PE（A，C，ε）≠?；（x0，y0）稱為（VP）的C（ε）-真有效點，如果x0∈D且y0∈F（x0）∩PE（A，C，ε）.

基于文獻［14］的思想，文獻［7］提出了如下的鄰近C（ε）-次似凸性概念，相似的廣義凸性概念也參見文獻［8-9］.

定義 3.1［7］設ε≥0，S?X.稱集值映射F：S?Y在S上是鄰近C（ε）-次似凸的，若cl cone（F（S）+C（ε））是凸集.

引理 3.1設C?Y為真星型co-radiant集滿足kern C≠?，則kern C是凸集.

引理 3.2設ε＞0，C?Y為真星型co-radiant集，int（kern C）≠?，則

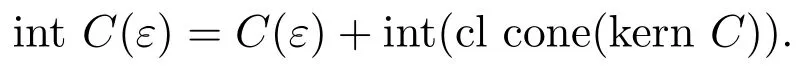
引理3.3設C?Y為真星型co-radiant集滿足int（kern C）≠?，μ∈（cl cone（kern C））+s，則μC也是真星型co-radiant集滿足int（kernμC）≠?且int（μC（ε））=μint C（ε）.

定理 3.1設 ε＞0，C?Y為真星型 co-radiant集且 int（kern C）≠?.如果 μ∈（cl cone（kern C））+s，（F，G）在X上是鄰近（C（ε）×P）-次似凸的，則（μF，G）在X上是鄰近（μC（ε）×P）-次似凸的.

證明由引理3.3易得定理3.1成立.

定理 3.2設 ε＞0，C?Y為真星型 co-radiant集，int（kern C）≠?.F：D? Y，y0∈F（D）.如果存在μ∈（cl cone（kern C））+s滿足則y0∈PE（F（D），C，ε）.

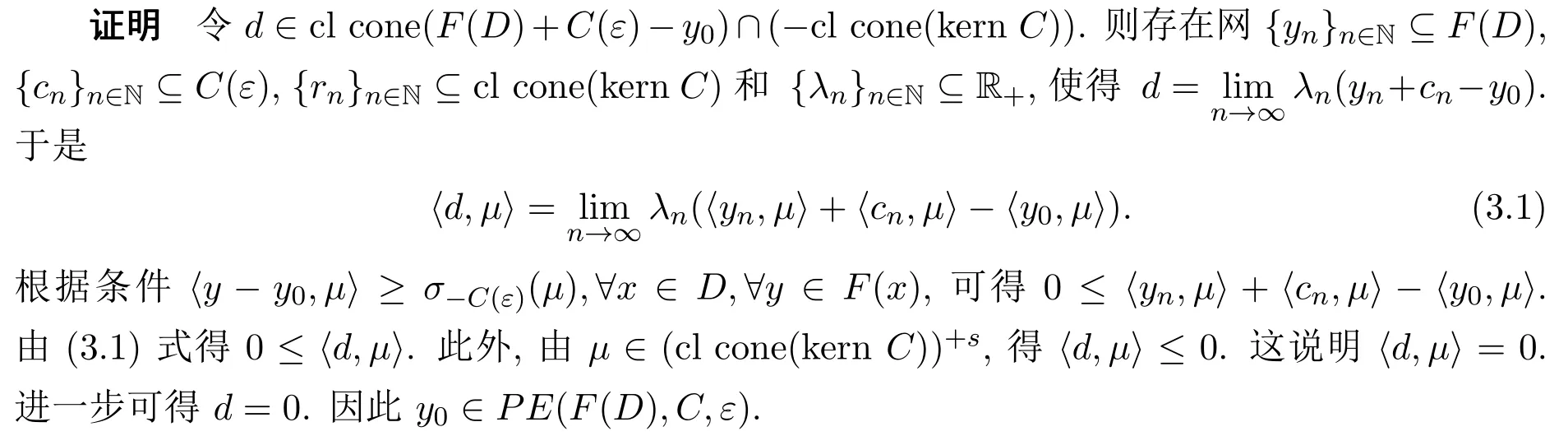
接下來，建立C（ε）-真有效解的Kuhn-Tucker型最優性必要條件和充分條件.

定理 3.3設ε＞0，C?Y為真星型co-radiant集，int（kern C）≠?.假設以下條件成立：

（i）（x0，y0）是（VP）問題的C（ε）-真有效點；

（ii）（F-y0，G）在X上是鄰近（C（ε）×P）-次似凸的；

（iii）cl cone（G（X）+P）=Z，

則存在μ∈（cl cone（kern C））+s和φ∈P+，使得

定理 3.4設ε＞0，C?Y為真星型co-radiant集滿足int（kern C）≠?.若x0∈D，且存在y0∈F（x0），μ∈（cl cone（kern C））+s和 φ∈P+滿足

則（x0，y0）是（VP）的C（ε）-真有效點.

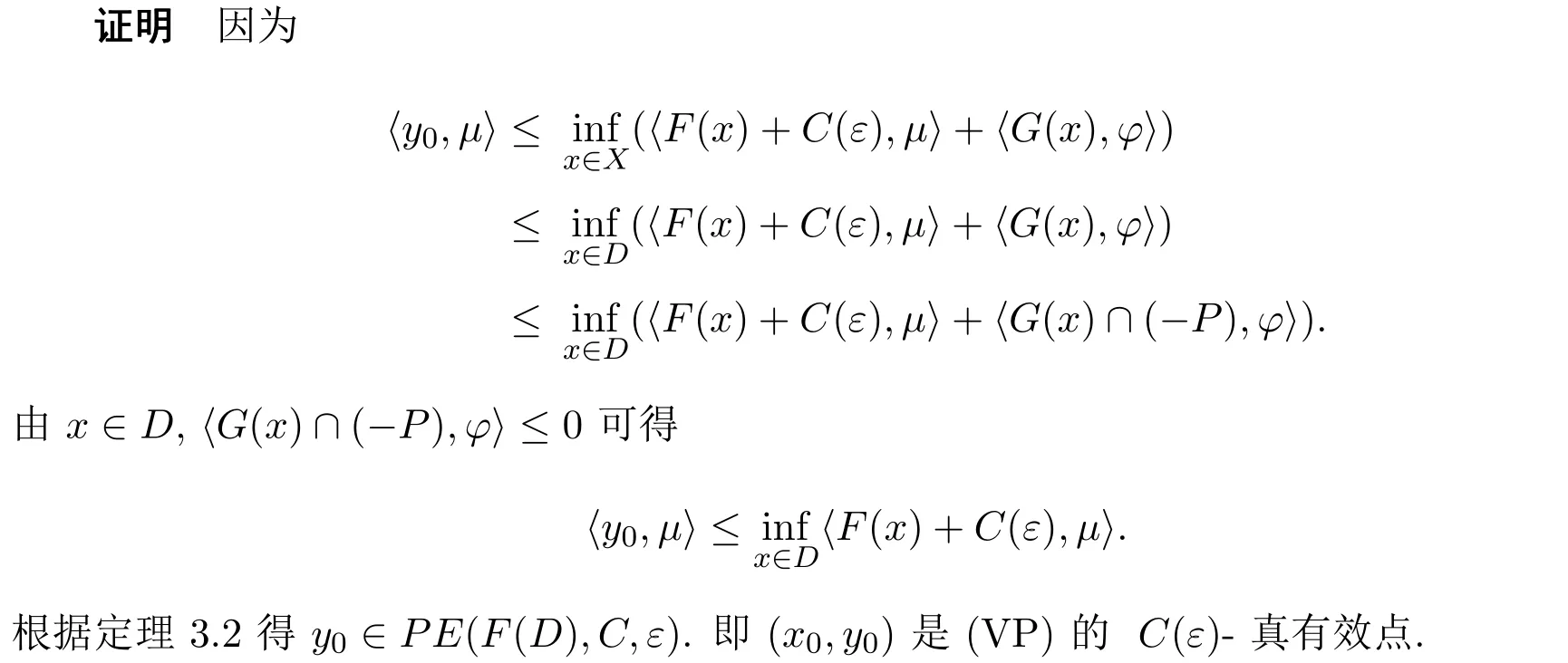
根據定理3.3和定理3.4下面的結論是顯然的.

推論 3.1設ε＞0，C?Y為真星型co-radiant集，且int（kern C）≠?.假設以下條件成立：

（i）（x0，y0）是（VP）的C（ε）-真有效點；

（ii）（F-y0，G）在X上是鄰近（C（ε）×P）-次似凸的；

（iii）cl cone（G（X）+P）=Z，

則（x0，y0）是（VP）的C（ε）-真有效點當且僅當存在μ∈（cl cone（kern C））+s和φ∈P+，使得

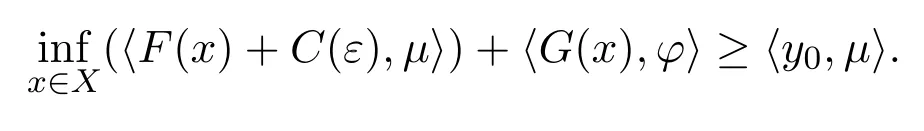
［1］Jahn J.Vector Optimization：Theory，Applications，and Extensions［M］.Berlin：Springer，2004.

［2］Chen G Y，Huang X X，Yang X Q.Vector Optimization［M］.Vol 541，Lecture Notes in Economics and Mathematical Sciences.Berlin：Springer，2005.

［3］Benson H P.An improved definition of proper efficiency for vector maximization with respect to cones［J］.Journal of Mathematical Analysis and Applications，1979，71（1）：232-241.

［4］Rong W D，Ma Y.ε-Properly efficient solutions of vector optimization problems with set-valued maps［J］.Operations Research Transactions，2000，4（4）：21-32.

［5］Gutiérrez C，Jiménez B，Novo V.A unified approach and optimality conditions for approximate solutions of vector optimization problems［J］.SIAM Journal on Optimization，2006，17（3）：688-710.

［6］Gao Y，Yang X M，Teo K L.Optimality conditions for approximate solutions of vector optimization problems［J］.Journal of Industrial and Management Optimization，2011，7（2）：483-496.

［7］Gutiérrez C，Huerga L，Novo V.Scalarization and saddle points of approximate proper solutions in nearly subconvexlike vector optimization problems［J］.Journal of Mathematical Analysis and Applications，2012，389（2）：1046-1058.

［8］Zhao K Q，Yang X M.E-Benson proper efficiency in vector optimization［J］.Optimization，2013，64（4）：1-4.

［9］Zhao K Q，Xia Y M.A kind of unified proper efficiency in vector optimization［J］.Abstract and Applied Analysis，2014（2014）：Article ID 636907，5 pages.

［10］Borwein J.Proper efficient points for maximizations with respect to cones［J］.SIAM Journal on Control and Optimization，1977，15（1）：57-63.

［11］Tiel J V.Convex Analysis［M］.New York：John Wiley and Sons，1984.

［12］Tanaka T，Kuroiwa D.The convexity of A and B assures int A+B=int（A+B）［J］.Applied mathematics letters，1993，6（1）：83-86.

［13］Tanaka T，Kuroiwa D.Another observation on conditions assuring int A+B=int（A+B）［J］.Applied Mathematics Letters，1994，7（1）：19-22.

［14］Yang X M，Li D，Wang S Y.Near-subconvexlikeness in vector optimization with set-valued functions［J］.Journal of Optimization Theory and Applications，2001，110（2）：413-427.

Kunh-Tucker optimality conditions for vector optimization problem in the sense of C（ε）-properly efficient solutions

Zhang Wanli，Zhao Kequan

（College of Mathematics Science，Chongqing Normal University，Chongqing401331，China）

In this paper，a kind of proper efficiency，named as C（ε）-proper efficiency，is proposed via co-radiant sets in a real locally convex Hausdorff topological linear spaces.By means of examples we illustrate that the C（ε）-proper efficiency is different from the proper ε-efficiency.and contains Benson proper efficiency as a special case.Furthermore，under the assumption of nearly C（ε）-subconvexlikeness，a Kuhn-Tucker necessary condition is derived，and by using scalarization theorem，a sufficient condition is also obtained.

vector optimization，C（ε）-proper efficiency，Kuhn-Tucker optimality condition

O221.6

A

1008-5513（2015）03-0323-08

10.3969/j.issn.1008-5513.2015.03.014

2014-11-18.

國家自然科學基金（11301574；11171363）；第二批重慶市高等學校青年骨干教師資助計劃；重慶市研究生科研創新項目（CYS14136）.

張萬里（1987-），碩士生，研究方向：最優化理論與方法.

2010 MSC：90C26，90C29，90C30