匹配組合網絡的寬直徑①

高珊

（湖北大學數學與統計學學院，湖北 武漢 430062）

圖的很多參數，如連通度和直徑，在圖論和組合數學本身十分重要，而且由于與通信網絡的容錯性和傳輸延遲密切關聯而被廣泛研究.當前，隨著超大規模集成電路技術和光纖材料科學的發展，針對大規模并行處理和圖論算法的需要，一些學者致力于研究圖的寬直徑，力求設計出稀疏、均勻且具有盡可能小的直徑和盡可能大的連通度的網絡，以提高互連網絡的可靠性、容錯性，減小網絡的通信延遲，并取得了一些較好的研究結果.筆者研究匹配組合網絡G(G0,G1;M)的寬直徑，并根據該網絡的結構性質，用點不交的最短路徑方法得到G(G0,G1;M)的寬直徑的上界估計式.

1 定義及預備定理

采用Bondy和Murty[1]中的術語和記號，并且只考慮簡單無向圖.我們用G=(V,E)表示一個圖，令u∈V(G)，NG(u)和dG(u)分別表示點u的鄰域和度.圖G中兩點u和v的距離dG(u,v)，定義為G的最短(u,v)-路的長度，如果沒有這樣的路存在，則令dG(u,v)=∞.圖G的直徑d(G)定義為G中任意兩點之間的最大距離.如果圖G不是完全圖Kn，那么G的連通度κ(G)定義為G中所有點分離集的最小頂點數，否則κ(Kn)=n-1.如果κ(G)≥k，那么G稱為k-連通的.

若一個圖G是k-連通的，則由Menger定理可知，對G中任何不同兩頂點u和v，G中存在k條點不交的(u，v)-路.

令G為ω-連通的，且0＜k≤ω.圖G的寬直徑及相關的概念定義如下：

定義1[2]對G中任何不同兩頂點u和v，圖G中從u到v的寬度為k的距離，簡稱k-距離，記為dk(G;u,v)，定義為最小整數d.換句話說，dk(G;u,v)是一個最小正整數d使得G中至少存在k條內點不交且長不超過d的(u,v)路.

定義2[2]圖G的寬度為k的直徑，簡稱k-直徑，記為dk(G)，定義為dk(G)=max{dk(G;u,v):?u,v∈V(G)},

顯然，d1(G)就是G的直徑d(G)，而且有d(G)=d1(G)≤d2(G)≤…≤dω-1(G)≤dω(G).

寬直徑的概念最先是由Hsu[3]，Hsu和Lyuu[4]，Hsu和Luczak[5]，Flandrin和Li[6]提出的.寬直徑是度量互聯網絡容錯性的重要參數，也是圖論的重要研究方向.一些圖的寬直徑，例如笛卡爾乘積圖等已被研究[1，3，6-9].

對一般圖G，給出dk(G)的值是困難的，因為這是NP完備問題.目前，只得到了一些dk(G)的上下界的估計式和一些著名的圖（結構簡單）的寬直徑.

下面我們也需要給出網絡傳輸延遲和容錯性的另一種類型的度量參數——Rabin數.

定義3設G是ω(≥ 1)連通圖，圖G的ω-Rabin數，記為rω(G)，定義為最小數r，使得對G的任何ω+1個頂點x,y1,…,yω，G中存在ω條內點不交且長度不超過r的(x,yi)路，i=1,2,…,ω.即G中存在扇Fω(x,Y)，使得每條路的長度至多為r，其中Y={y1,…,yω} .

顯然，如果1≤ω≤κ(G)，則rω(G)有確定的值，且d(G)=r1(G)≤r2(G)≤…≤rω-1(G)≤rω(G).

2 匹配組合網絡G(G0,G1;M )

令r和n都是正整數，且r≥3.令G0和G1是兩個圖，且|V(G0)|=|V(G1)|=n.圖G(G0,G1;M)的 頂 點 集 定 義 為V(G0)?V(G1)，邊集為E(G0)?E(G1)?M，其中M是G0和G1頂點間的一個任意完美匹配（見圖1）.則G(G0,G1;M)是一個頂點數為2n，邊數為|E(G0)|+|E(G1)|+n，具有完美匹配的圖.例如，若G0=G1=Qk，則存在M使得G(G0,G1;M)=Qk+1；或者若G0=G1=CQk，則存在M使得G(G0,G1;M)=CQk+1，這里Qk表示k-維超立方體(hypercube)，CQk表示k-維交叉超立方體(crossed hypercube).

圖1 G0和G1頂點間的匹配圖

許多著名的網絡，例如超立方體、螺旋立方體、星圖等等，能通過連接兩個低維的網絡擴展為高維的網絡，下面的匹配組合網絡就是這樣的擴展例子[7-8].

圖G的一個完美匹配就是邊的集合M，滿足沒有兩條邊是有公共頂點的，并且G中的每個頂點都在M中.顯然，如果圖G有完美匹配，那么圖G的階一定是偶數.

本文中將討論分析匹配組合網絡G(G0,G1;M)的寬直徑.為了方便，下面用u→Pk v表示從u到v的路Pk，u→v表示邊uv.

3 網絡G(G 0,G1;M )的寬直徑

為了簡單起見，下面我們把G(G0,G1;M)，V(G0)，V(G1)分別簡記為G,V0,V1.對任意的點u∈V(G)=V0?V1，即u∈Vi(i=0,1) ，用uˉ∈V1-i表示與u相鄰的頂點.顯然，有uuˉ∈M.

定理3.1令G0和G1是兩個頂點數相同的連通圖，且κ(G0)=κ(G1)=ω，那么κ(G)≥ω+1.

定理3.1的證明由Menger-Whitney判定準則，我們只需在G中構造ω+1條內點不交的(u,v)-路R1,…,Rω,Rω+1.對于圖G的任意兩點u和v，不妨假設u∈V0.我們考慮兩種情形.情形1v∈V0.

因為G0是ω-連通的，故由Menger定理可知，G0中存在ω條內點不交的( )u,v- 路P1,P2,…,Pω.另一方面，G1中存在一條(),ˉ- 路 Q.令

則R1,…,Rω,Rω+1是G中內點不交的路.

情形2v∈V1.

令U?Vi{u} ，V?V1-i{v}，其中U={u1,u2,…,uω} ，V={v1,v2,…,vω} .因為G0和G1是ω- 連通的，Gi中存在(U,u)- 扇Fω(U,u)={W1,W2,…,Wω} ，其中Wk的長度最多為rω(Gi)；G1-i中存在 (V,v)-扇Fω(V,v)={T1,T2,…,Tω} ，其中Tk的長度最多為rω(G1-i).

如果v=ˉ，那么我們選擇U，V使得vvk∈E(G1-i) ，vk=，其中k=1,2,…,ω.令

否則，我們選擇U，V使得其中k=1,2,…,ω-1.令

易驗證，上述情形中構造的路R1,…,Rω,Rω+1是G中內點不交的路.證畢.

推論3.2令G0和G1是頂點數相同的兩個圖，G=G(G0,G1;M).如果κ(G0)=κ(G1)=δ(G0)=δ(G1)=ω，那么

推論3.2的證明由定理3.1，有κ(G)≥ω+1.由Whitney不等式，可以得到

因此，κ(G)=ω+1.證畢.

定理3.3令G0和G1是頂點數相同的兩個圖，G=G(G0,G1;M).如果κ(G0)=κ(G1)=δ(G0)=δ(G1)=ω，其中i=0,1，那么dω+1(G)≤max{2 +rω(G0),2+rω(G1),dω(G0),dω(G1) }.

定 理3.3的 證 明由 推 論3.2，G是(ω+1)- 連 通 的.因 此dω+1(G)有 確 定 的 值.令d=和v是G中不同兩個頂點.下面，我們只需在G中構造(ω+1)條長度不超過d的內點不交的(u,v)-路.

情形1u,v∈Vi(i∈{0 ,1}).

圖2 G0，G1關系示意圖

因為Gi是ω-連通的，由Menger定理，Gi中存在ω條內點不交的(u,v)-路P1,P2,…,Pω，使得Pk(1 ≤k≤ω)的最大長度為dω(Gi).令Q是G1-i中最短(uˉ ,vˉ)- 路(參見圖 2)，

則由rω(Gi)≥d(Gi)可知，

情形2u∈Vi，v∈V1-i.

令

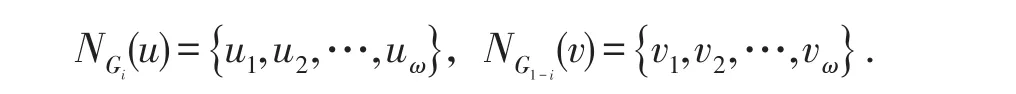
則

如果v≠uˉ，那么G1-i中存在一條最短路假設v1在Q上.令則因為Gi是ω- 連通的，Gi中存在 (U,u)-扇Fω(U,u)=其中Wk的長度最多為rω(Gi) ，參數關系見圖3（b）.

則由rω(Gi)≥d(Gi)可知，

證畢.

本文中主要討論了匹配組合網絡的寬直徑.匹配組合網絡是著名的互連網絡，給出了組合匹配網絡G( )G0,G1;M的寬直徑的上界，為度量該網絡的性能提供了重要的依據.

圖3 G0，G1匹配組合網絡圖

[1]Bondy JA，Murty USR.Graph theorywith applications[M].London:Macmillan，1976.

[2]徐俊明.組合網絡理論[M].北京：科學出版社，2007：241.

[3]Hsu DH.On container width and length in graphs，groups，and networks[J].IEICE Trans Fundam，1994，E77A:668-680.

[4]Hsu D H，Lyuu Y D.A graph-theotetical study of transmission delay and fault tolerance[C].In Proc of 4thISMM International Confrenceon Paralleland Distributed Computingand systems，1994.

[5]Hsu DH，Luczak T.Noteon thek-diameterofk-regulark-connected graphs[J].DiscreteMath，1994，132:291-296.

[6]Flandrin E，LiH.Mengerian properties，Hamiltonicity and claw-free graph[J].Networks，1994，24:660-678.

[7]Chen Y，Jimmy JM.Tan Restricted connectivity for three familiesof interconnection networks[J].Appl Math Comput，2007，188:1848-1855.

[8]Chen Y，Jimmy J，Tan M，etal.Super-connectivity and super-edge-connectivity for some interconnection networks[J].Appl Math Comput，2003，140:245-254.

[9]BanicˇI，?erovnik J.Wide diameter of Cartesian graph bundles[J].Discrete Math，2010，310:1697-1701.