點焊機器人路徑規劃及應用

蘭斌

摘要：針對目前白車身焊接機器人路徑規劃不合理的問題，總結歸納了不同算法的優點和不足，改進了貪婪算法容易進入局部最優的缺陷，并提出一種基于刪除最大的距離的路徑規劃新算法。結合實際生產線車身側圍焊點布局，用兩種算法作了對比分析，最后用DELMIA軟件進行了實例驗證。

關鍵詞：白車身；路徑規劃；TSP問題；貪婪算法

前言

隨著社會經濟和科學技術的快速發展，焊接機器人技術不管是在研究領域還是工程實踐領域都有了很大的提高。焊接機器人在白車身焊接上的運用，很大程度上提高了焊接質量，改善了工人的勞動條件，提高了生產效率。而點焊以其獨特的成本優勢使得它成為了目前國內的各大汽車組裝廠的主要焊接方式。然而在實際生產過程中，傳統的點焊機器人一般采用路采用在線示教方法對機器人的路徑進行規劃和仿真，由于工作任務和工作環境的復雜性，并且多臺機器人還需避免相互干涉和碰撞，因此，實際工作中需對機器人反復調試，從而會導致機器人路徑的設計工作量大、效率低，且不便于優化、無法并行工作[1]。本文在對點焊機器人和車身進行虛擬建模的基礎上，提出基于刪除最大距離的新型算法，并編寫算法實現程序，在DELMIA軟件仿真中實現點焊機器人路徑自動規劃，在很大程度上提高點焊機器人的路徑規劃設計效率，提高了點焊機器人的工作效率。

1.白車身焊接特點

焊接工藝是整車制造廠四個工藝之一，是白車身加工制造的重要環節，白車身焊接包括對發動機倉，前底板，后地板，側圍，頂棚和五門一蓋等零部件或零部件總成的裝配焊接。本文就側圍工位機器人點焊具有如下特點：

1.1工作環境復雜。側圍工位主要運用點焊機器人進行自動化焊接，焊接工位包括機器人群組，工裝夾具，車身工件，傳輸裝置等。機器人的活動范圍是有限的，特別是在多臺機器人在同一工位上執行操作的時候，往往會對機器人的路徑規劃造成很大的困難。

1.2焊點數量多。每個焊接工位上面有多臺機器人，每臺機器人負責的焊點一般二十個左右。

1.3使用的焊接方法多。包括電阻點焊、激光焊、CO2氣體保護焊等等。其中電阻點焊因其獨特的成本優勢，良好的焊接性能，是目前國內整車廠中應用最廣泛的焊接方式。

1.4對焊接技術要求高。對焊接產品有高的尺寸精度要求，對焊縫接頭有高的性能要求，對批量化焊接生產有高品質的要求，對焊接過程有高節拍、高效率的要求[2]。

一臺整車的焊點數有4000～5000個，每個人或是每臺機器人負責的焊點一般二十多個，因此對車身焊點的路徑規劃顯得很重要，一個好的路徑不僅能節省人力、物力、財力，更重要的是能節省時間，提高效率和生產效益。

2.路徑優化數學模型及優化算法

2.1.TSP旅行商問題基本思想和數學模型

旅行商問題（TSP）是組合優問題中典型的NP-完全問題，是許多領域內復雜工程優化問題的抽象形式。TSP問題是這樣描述的：設有n個城市，一個旅行商從其中一個城市出發，最后回到出發的城市，其余n-1個城市，有且只能經過一次，目標是所經過的路徑距離最短，這就是著名的旅行商問題（TSP）。用圖論的語言來描述，正權圖G=（V，E，W）中，包含圖G中每個點至少一次的一條環路稱為旅行商環路，一條具有最小權和的旅行商環路稱為最佳旅行商環路，求最佳旅行商回路的問題稱為旅行商問題（TSP）。而具有最小權和的哈密頓回路稱為最佳哈密頓回路問題[3]。

旅行商問題（TSP）的數學模型描述如下：

設G=< V，E> 為賦權圖，V={1，2，...，n}為頂點的集合，E為邊的集合。各頂點間距離 已知（ >0， ，i，j V），并設

這里，S是V頂點集合的任意的一個子集，第一個約束意味著對每個頂點而言，僅有一條邊進和一條邊出，后一約束則保證了沒有任何子回路解的產生。于是，滿足上述約束的解構成了一條哈密頓回路。

2.2.改進貪婪算法及實現

求解TSP旅行商問題的解法很多，主要分為精確解法和近似解法兩大類。精確算法能得到TSP的精確解，對于TSP的一些特殊情況，業已研究出一系列非常優美的結果，如：機器排序問題（Gilmore等，1964）、二分圖情形（Lawler，1971）、平面TSP中的一些特例（Burkard，1989），等等。可解情形的結果都已經成為了成熟的定理。還有一些其他的精確算法如：線性規劃算法、動態規劃法、分之界定算法等。近似算法包括插入算法，最近鄰算法，Clark&Wright算法，雙生成樹算法等。到了八十年代往后，出現了很多智能算法，如：神經網絡算法，模擬退火算法，遺傳算法，蟻群算法等[4]。上述算法各有各的特點和應用范圍，精確算法能得到TSP的精確解，但是當維數n增大時，運算所用的時間成指數級增長，近似算法能較好的解決時間復雜度的問題，但是要犧牲一定的精度，智能算法則能在大型復雜工程問題時表現出其獨特的優勢，得到滿足精度要求的解。

貪婪算法又叫貪心算法。貪婪算法（greedy algorithm）是一種解決最優化問題的近似方法[5]。它是一種逐步構建最優解的方法，在對問題求解時，總是做出當前看來最好的選擇。，貪婪算法并不要求對所有問題都能得到整體最優解，而是某種意義上的局部最優解，在大量實際應用中，能得到問題的整體最優解或者是整體最優解的近似解[6]。

貪婪算法在每個決策階段作出的決策不可更改，作出貪婪決策的依據稱為貪婪準則（greedy criterion），也稱貪婪因子。在路徑規劃中，路徑的最小值即為貪婪因子。具體的算法流程如下：

Step1：輸入n*n維距離矩陣D（對角元素為0的對稱矩陣）和解矩陣X（和D矩陣同維數的0矩陣）。

Step2：選擇任一頂點作為出發點，比較其他頂點與當前點的距離，選擇最小距離的頂點相連。解矩陣X中對應連接的邊賦值為1.

Step3：若最小距離的頂點已經在已連接的路徑中，則賦值這個距離為無窮大，循環Step2.最終得到解矩陣X。

3.基于刪除最大距離算法技術方案研究

總結以上算法，本文作者提出了一種基于刪除最大距離的焊接機器人路徑優化的近似算法。應用于較小維數的路徑優化，新算法的時間復雜度為O（ ），能較快的收斂，并且思路簡單，操作方便。基于刪除最大距離算法與貪婪算法有相似之處，也容易產生局部解，經過改進，較小維數上能避免局部最優解的產生。在某種程度上，解要比貪婪算法更優。具有一定的應用價值。

基于刪除最大距離算法流程如下：

Step1.構造一個n*n維距離矩陣D（對角線元素為0的對稱矩陣）和解矩陣X（和D矩陣同維數的全1矩陣）。并對距離矩陣中元素從小到大進行排序。

Step2.選出最長距離，即最長邊，兩個頂點如果各連接的邊數多于兩條，則刪除當前最長邊，并把解矩陣中的當前位置元素賦值為0.循環直至所有滿足要求的邊都刪除完為止。

Step3.在執行完Step2之后會出現兩種情況：

3.1所有頂點都連接兩條邊，滿足哈密頓回路，刪除最長邊，形成開環，得到需要的解矩陣。

3.2某一個或多個頂點連接邊數多余兩條或者形成局部環，形成局部最優解。

①某一個頂點或多個頂點連接邊數多余兩條處理如下。

找出當前頂點所連接邊中最長的一條，在保證當前頂點連接邊的另一頂點所連接邊數大于一條時，刪除當前邊，直到當前頂點所連邊數等于1為止。

②形成局部環處理。刪除局部環中最長邊。

③至此形成了兩條以上的由數個頂點連接的開環。找出每條開環的端點，計算不在同一條環的各個端點之間的距離，選擇最短的連接，直至所剩端點為2為止，形成一條開環鏈。得到需要的解矩陣。

基于刪除最大距離算法流程圖如下：

4.仿真實例驗證

DELMIA數字制造解決方案可以使制造部門設計數字化產品的全部生產流程，在部署任何實際材料和機器之前進行虛擬演示。DELMIA軟件由兩個相互關聯的獨立軟件DPE（Digital Process Engineer ）和DPM（Digital Process Manufacture）組成。

Robotics模塊是一個基于物理的、可伸縮的三維機器人仿真解決方案。可用于對復雜的，多設備機器人工作單元進行建模和離線編程。利用Robotics可快速和圖形化的構造各種應用工作單元作業，如焊接、噴涂、搬運、打磨和裝配等。下圖表示利用DELMIA/Robotics對車身焊接側圍某工位的路徑仿真畫面。

本文的焊點分布來自某整車制造企業焊裝生產線側圍總成工位SJ12機器人焊接焊點布局。焊接方式為點焊，生產節拍為70S。其中兩層焊焊點10個，三層焊焊點7個。本文采用基于刪除最大距離算法所求路徑與改進貪婪算法和某整車制造企業生產線生產的路徑進行對比，對比的標準是路徑總和最短。

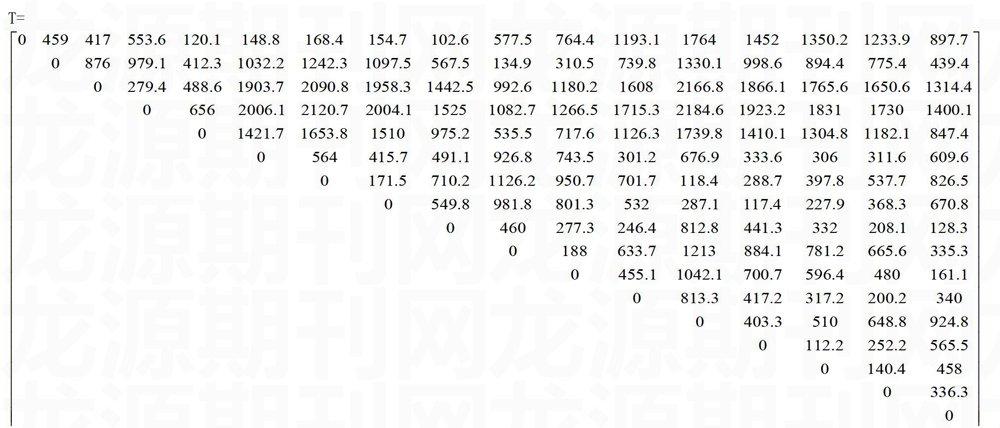
距離矩陣D是通過焊點坐標計算出來的，取D的上三角T矩陣如下：

基于刪除最大距離算法的距離總長和貪婪算法距離總長對比，從表1中可看出，貪婪算法從1～17作為起始點，刪除最大距離算法較貪婪算法更優。

5.結論

路徑規劃的算法有很多，針對不同的具體情況，各有各的優勢和不足。本文解決了貪婪算法容易陷入局部最優的問題，并提出了一種基于刪除最大距離的新算法。使用matlab編程實現，調用DELMIA/Robotics模塊對汽車車身側圍某一工位點焊機器人路徑進行了仿真，兩種算法進行對比分析。分析結果表明，基于刪除最大距離的算法能比較好的優化路徑，滿足路徑規劃的要求。

參考文獻：

[1]張勇智，韓贊東.白車身裝焊單元點焊機器人路徑規劃研究.機械設計與制造，2006.

[2]海江，羅生斌.白車身側圍工位焊接機器人路徑優化研究[J].制造業自動化，2005，27（7）：35-38.

[3]管琳，白艷萍.用分支定界法求解旅行商問題.中北大學學報，2007，28（2）：104-107.

[4]馬良.旅行推銷員問題的算法綜述.數學的實踐與認識，2000，30（2）：156-165.

[5]Jean-claude Agnese，Pascal Brousse.Sch- eduling Techniques for a Constellation Visibil-ities[R].ASS98-303，1998.

[6]http：//baike.baidu.com/view/298415.htm？fromId=1628576.