基于Stochastic Kriging的柔性機翼穩健性優化設計

劉艷，白俊強，華俊，2，劉南，王波

1.西北工業大學航空學院，陜西西安 710072；2.中國航空研究院，北京 100012 3.中國航天空氣動力技術研究院，北京 100074

基于Stochastic Kriging的柔性機翼穩健性優化設計

劉艷1，白俊強1，華俊1，2，劉南1，王波3

1.西北工業大學航空學院，陜西西安 710072；2.中國航空研究院，北京 100012 3.中國航天空氣動力技術研究院，北京 100074

采用隨機代理模型方法對柔性機翼氣動外形進行穩健性優化設計。相比確定性優化設計，穩健性設計能夠考慮設計變量和參數的擾動，保持設計結果在不確定性影響下的性能穩定。采用高精度的氣動/結構耦合求解器（耦合Navier-Stokes方程和結構靜力學方程）分析柔性機翼的變形情況和氣動效率。為了提高優化效率，建立隨機Kriging（Stochastic Kriging，SK）代理模型，將確定性的Kriging代理模型發展到隨機空間，通過有限次輸入得到數據的固有不確定性。對柔性M6機翼的氣動外形進行穩健性優化設計，結果表明：相比確定性代理模型的穩健性優化結果，應用隨機代理模型的優化結果的設計點阻力系數減小2.8 counts，在可變馬赫數范圍內阻力系數均值減小3.2 counts，優化結果具有較高的設計點氣動效率和阻力發散特性，并且優化后構型的翼根彎矩有明顯減小，體現隨機代理模型在穩健性優化設計系統中的優勢，同時也說明建立的SK代理模型具有較高的預測精度。

柔性機翼；穩健性優化；靜氣動彈性力學；隨機Kriging代理模型；Navier-Stokes方程

目前工程中常用的優化設計方法是確定性優化設計，但該方法中設計變量、目標函數和約束函數均為確定性問題，因此不能夠反應工程設計、產品制造以及服役環境對設計結果的影響，其中客觀存在大量不確定性因素會對設計方案產生影響，而傳統優化設計的最優解對于這些不確定性因素非常敏感［1-4］。與傳統的確定性優化［5］相比，穩健性優化［6-7］的一個顯著特點就是在優化過程中考慮不確定性因素的存在，減小設計目標對不確定性因素的靈敏度，保持設計結果在不確定性影響下性能穩定。穩健性設計的求解方法可以分為確定性方法和隨機化方法兩類。確定性方法［8］是將不確定性問題通過一定的分析轉化為確定性問題，然后利用相關優化算法求解。而通過直接優化擾動量和約束的方法來處理不確定性問題，因此也有時被稱為數值優化方法。隨機化方法［9-10］通常都是基于直接搜索法開展的研究，不需要顯式的一階或二階導數，而只需得到下一個位置處的目標函數響應，有效減少了對問題的依賴性。

由于問題規模爆炸式增加，考慮不確定性的穩健性設計計算量很大。為了提高效率，可以將隨機化方法與各種代理模型相結合以處理穩健性設計問題。主要是根據一定數量的離散樣本數據，通過構造響應的代理模型進行目標特性分析，在保證一定分析精度的基礎上大幅縮減計算量，進而加快整個設計系統的效率。這種方法由于相比傳統的蒙特卡羅模擬法（Monte Carlo Simulation，MCS）計算量小，可以得到可靠的低階矩信息等優點，在不確定性領域得到了眾多關注。

綜上，本文針對柔性機翼在飛行狀態不確定性情況，以應用較多的Kriging代理模型為原型建立隨機Kriging（Stochastic Kriging，SK）代理模型［11］，構建基礎問題，進行統計學推導以及確立相關參數求解方案，得到可靠的估計均值和方差，并通過基礎算例驗證這一方法在不確定性問題中較強的實用性。通過與基于確定性Kriging（deterministic Kriging，DK）代理模型的穩健性優化結果進行研究對比，驗證隨機代理模型在穩健性優化設計中的優勢。

1　理論基礎

1.1氣動/結構耦合理論基礎

由于要研究考慮飛行狀態不確定性影響的柔性機翼設計，需要機翼的靜彈性分析方法能夠捕捉不同飛行狀態下對流場造成的影響。因此建立耦合雷諾平均Navier-Stokes（RANS）方程和結構靜力學方程的高精度靜氣動彈性分析方法。氣動模型與結構模型之間載荷傳遞、彈性變形插值采用RBF插值方法進行，參考文獻［11-12］中有詳細介紹，此處僅給出靜氣彈分析流程如圖1所示，圖中CFD求解器為求解RANS方程，CSD求解器采用柔度影響系數矩陣方法，收斂條件為兩次彈性變形差小于給定誤差值，動網格采用四元數方法，載荷傳遞與位移插值均采用徑向基函數插值方法。

圖1　靜氣彈分析流程圖

1.2有限樣本的Stochastic Kriging建模

考慮不確定性的重復樣本點的情況下，將DK代理模型從確定性空間轉化到隨機空間中去［10］。為了解決包含各處非均等的不確定性和有限采樣點的問題，對空間中的隨機樣本將通過如下形式表示：

式中，ε（x）被定義為固有不確定性，用來表示擾動項，并被假設為正態分布，εj（x）是固有不確定性的一個實現，表示的是在x處重復樣本的擾動，并且被假設為與其他重復樣本的固有和非固有不確定性M（x）之間相互獨立，η（x）代表的是固有不確定性的方差。這里的輸入變量為若干組（xi，Yj（xi），Ni；i =1，2，…，n），其中Ni表示在位置xi處的重復樣本的個數，這里的Ni是有限值，各個位置處樣本的均值可以相應的表示為

此方法也可采用最優線性估計的形式進行預測，以得到未知位置的均值：

式中，wi（t）表示的是賦予各已知位置均值的權值量，也就是通過已知均值的權重來估計未采樣位置處的均值。對于不確定性的Stochastic Kriging模型［10］均方差的構建形式可表示為

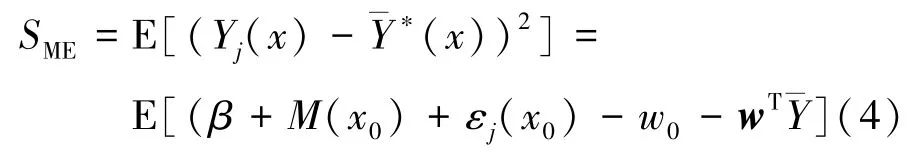
在對均方差的構建中，很明顯，重復樣本的固有不確定性信息被考慮進模型的構建過程中，以表示假設的真值和估計的形式。通過對公式（4）進行展開：

顯然，公式（5）中平方和展開的最后一項為零。根據上述獨立性假設，公式（5）即可寫為

對公式（6）的推導中，比較有代表性的一項可以展開為

式中，p、q表示的是輸入變量的某一位置，1≤p、q≤n。而后利用各重復樣本之間相互獨立的假設，公式（7）可以展開為

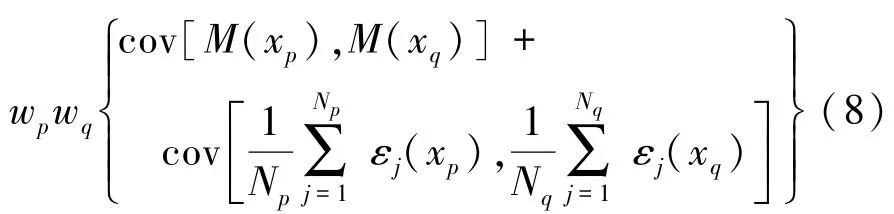
為了簡化公式中的符號，基于二階平穩假設［14］的假設，這里先將（8）式簡寫為如下的形式

2　基于穩健性設計的柔性機翼設計方法

建立的SK代理模型通過對基礎問題的構建、統計學推導以及相關參數求解方案的確立，得到了可靠的估計均值和方差，下面通過算例驗證了這一方法在不確定性問題中較強的適用性。柔性機翼穩健性優化設計流程如圖2所示。

圖2　穩健性優化設計流程圖

3　算例分析

本節用設計實例論述SK代理模型的可行性和魯棒性。以M6機翼為初始構型，設計點狀態為：Ma =0.84，Cl=0.271 54，Re=1.172×107，考慮來流馬赫數不確定性變化范圍Ma∈［0.82，0.83，0.84，0.85，0.86］。3.1節采用基于DK代理模型進行穩健性優化得到優化解。在3.2節應用SK代理模型進行柔性機翼的穩健性設計得到優化解。3.3節對3.1、3.2節的最優結果進行對比，并對結果進行分析。所有優化設計在滿足機翼體積不減小的約束條件下進行。

采用改進的FFD參數化方法［14］，該方法克服了原始FFD方法的設計變量相關性強的缺點，適用于精細化外形參數化，FFD控制框及控制點如圖3所示，共有3個控制截面，每個剖面有12個控制點控制z坐標，共36個控制點。再加外側2個剖面的扭轉角以及機翼后掠角，因此共有39個設計變量（xi，i=1，2，…，39）。設計變量范圍見表1，表中ID代表設計變量序號，lb代表設計變量變化的下限，ub代表設計變量變化的上限。

表1　39個設計變量范圍

圖3　FFD控制框及控制點

3.1基于確定性代理模型的穩健性優化

應用DK代理模型對柔性M6機翼在滿足容積約束條件下，考慮馬赫數不確定變化范圍Ma∈［0.82，0.83，0.84，0.85，0.86］時，進行穩健性優化設計，提高設計點的氣動特性，同時改善優化后機翼的阻力發散特性。

優化模型可表述為：

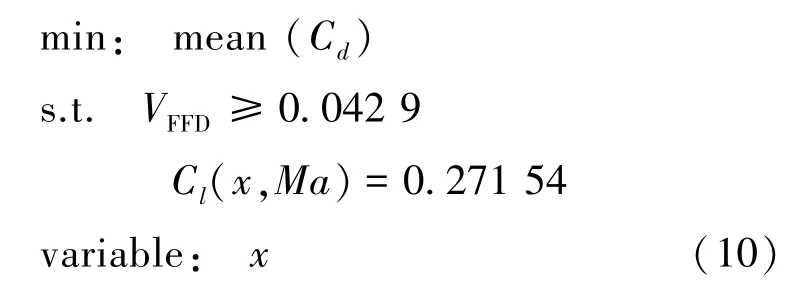
在設計空間內生成869個樣本點，選取19個為測試樣本點，其余850個構建改進的Kriging代理模型。應用改進的遺傳算法每代種群數為300個，進化代數為30代，在保證機翼體積不減小的情況下進機翼的穩健性優化設計。優化結果在3.3節中進行詳細討論。

3.2基于隨機代理模型的穩健性優化

基于構建的SK代理模型對M6機翼進行保證容積約束的穩健性優化設計，利用構建的優化系統在給定的約束條件下改善阻力發散特性。設計狀態為馬赫數范圍Ma［0.82，0.83，0.84，0.85，0.86］，優化的目標為降低阻力系數在擾動范圍內的均值和方差。優化模型可表述為：

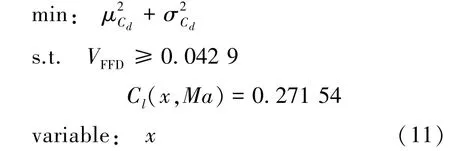
式中

為保證與使用確定性代理模型進行優化設計的采樣個數相同，將選用3.1節相同樣本點和優化算法。與運用確定性代理模型不同的是，在不同設計變量處進行馬赫數變化區間內5次均勻分布重復采樣建立隨機代理模型，通過在不同設計變量處的均值和方差作為SK模型的輸入變量，得到設計變量在未知位置處的響應均值和方差。

選取869個樣本點中19個作為測試樣本點，用于驗證SK代理模型是否合理。圖4給出SK代理模型預測的均值、方差與實際計算結果的對比曲線，結果吻合得很好，證明建立的SK代理模型的精度可以滿足之后的穩健性優化設計的需求。

圖4　SK代理模型預測的阻力均值與方差

3.3結果分析

圖5為優化前后幾何模型對比圖。

圖5　優化前后幾何模型對比

可以得出優化后構型的后掠角均增大，而SK模型優化結果的后掠角最大。

圖6為阻力發散特性曲線對比可得，2種優化結果在設計點處的阻力特性均得到改善，并且優化后阻力發散特性均得到明顯提高。通過DK代理模型和SK代理模型的優化結果對比曲線可得，SK代理模型的結果明顯優于DK代理模型，SK模型對隨機問題表現出了更強的預測能力。

圖6　阻力發散特性曲線對比

表2給出DK代理模型優化解在設計點位置阻力降低21.56%。在5個馬赫數阻力系數均值降低21.33%，方差降至2.149×10-8。SK模型優化解在設計點位置阻力降低23.30%，在可變馬赫數范圍為阻力系數均值降低23.23%，方差降至5.543 ×10-9。

表2　DK、SK代理模型穩健性優化結果對比

圖7為0.84馬赫數下運用DK代理模型和SK代理模型進行的穩健性優化設計結果在2個典型剖面的壓力分布對比，優化構型消除了機翼上表面激波，壓力分布恢復平緩。優化后機翼前緣峰值有所降低，有利于阻力發散特性改善有利，應用SK代理模型優化結果的峰值比DK代理模型優化的結果要低。

圖8為優化前后機翼考慮柔性變形后無量綱翼根彎矩的對比曲線。由圖中可得：采用DK代理模型優化解的翼根彎矩較原始構型有所增加，而采用SK代理模型優化解則明顯減小。可以得出，SK代理模型優化后構型沒有增加結構的要求下，明顯降低了翼根剖面的彎矩。

圖7　典型剖面壓力系數曲線對比圖

圖8　無量綱翼根彎矩對比曲線

4　結 論

通過研究柔性機翼的基于DK與SK穩健性優化設計結果的對比，可看出基于SK代理模型的穩健性優化設計更能有效提高柔性機翼的阻力特性及阻力發散特性。應用SK代理模型在優化過程中考慮不確定因素的存在，可以有效解決穩健性優化設計問題。SK代理模型優化結果較DK代理模型優化結果在設計點處阻力系數減小2.8 counts，在可變馬赫數范圍內阻力系數均值減小3.2 counts。同時SK代理模型穩健型優化后機翼對翼根彎矩有明顯減小。顯示出所構建SK代理模型在不確定性問題的研究中較DK代理模型有優勢。

［1］ Zang T，Hemsch M J，Hilburger M W，et al.Needs and Opportunities for Uncertainty-Based Multi Disciplinary Design Methods for Aerrospace Vehicles［R］.NASA TM-2002-211462

［2］ Zeeshan Q，Yunfeng D，Rafque A F，et al.Multidisciplinary Robust Design and Optimization of Multistage Boost Phase Interceptor［R］.AIAA-2010-2920

［3］ Yu X，Du X.Reliability-Based Multidisciplinary Optimization for Aircraft Wing Design［J］.Structure and Infrastructure Engineering 2006，2（3/4）：277-289

［4］ Sues R H，Oakley D R，Rhodes G S.MDO of Aeropropulsion Components Considering Uncertainty［R］.AIAA-1996-4062

［5］ Queipo N V，Haftka R T，Shyy W，et al.Tucker Surrogate-Based Analysis and Optimization［J］.Progress in Aerospace Sciences，2005，41：1-28

［6］ Schuelera G I，Jensen H A.Computational Methods in Optimization Considering Uncertainties—An Overview［J］.Computer Methods in Applied Mechanics and Engineering，2008，198（1）：2-13

［7］ Andradottir S.A Review of Simulation Optimization Techniques［C］∥Proceedings of the 1998 Winter Simulation Conference，IEEE，Piscataway，NJ，1998：151-158

［8］ Jin R，Du X，Chen W.The Use of Metamodeling Techniques for Optimization Under Uncertainty［J］.J Struct Multidisciplinary Optim，2003，25（2）：99-116

［9］ Hans Georg Beyer，Bernhard Sendhoff，Robust Optimization—A Comprehensive Survey［J］.Computer Methods in Applied Mechanics and Engineering，2007，196（33/34）：3190-3218

［10］Wang B，Bai Junqiang，Hae Chang Gea.Stochastic Kriging for Random Simulation Metamodeling with Finite Sampling［C］∥39th Design Automation Conference（DAC），Portland，Oregon，2013

［11］Liu Y，Bai J Q，Hua J.Static Aeroelasticity Analysis of High Aspect Ratio wing and the Jig-Shape Design Based on Multi-Block Structural Grid［J］.Advanced Engineering and Materials，2013，302：377-383

［12］劉艷，白俊強，華俊，等.非線性流固耦合分析方法研究［C］∥中國力學大會，2013

Liu Y，Bai J Q，Hua J，et al.An Approach to the Nonlinear Fluid-Structure Coupling Technical［C］∥CCTAM2013，2013（in Chinese）

［13］Journel A G，Huijbregts CJ.Mining Geostatistics［M］.London，Academic Proess，UK，1978

［14］Lamousin H J，Waggenspack W N.NURBS-Based Free-Form Deformations［J］.IEEE Computer Graphics and Applications，1994，11：59-65

Robust Optimization of Flexible Wing Using Stochastic Kriging Surrogate Model

Liu Yan1，Bai Junqiang1，Hua Jun1，2，Liu Nan1，Wang Bo3

1.College of Aeronautics，Northwestern Polytechnical University，Xi′an 710072，China 2.Chinese Aeronautics Establishment，Beijing 100012，China 3.China Academy of Aerospace Aerodynamics，Beijing 100074，China

The stochastic surrogate model method is applied in the robust optimization design of flexible wing.Comparing with deterministic optimization design，robust design can take into consideration the disturbances of design variables and parameters.Therefore，the performance of design results can be kept stable under uncertainties.A High-fidelity fluid-structure coupling solver（coupled Navier-Stokes equations and static structure equations）is used to analyze the deformation and aerodynamic characteristics of flexible wing.In order to enhance optimization efficiency，Stochastic Kriging（SK）surrogate model，which extends deterministic Kriging（DK）surrogate model into stochastic space，is built.The intrinsic uncertainties of data is acquired by finite number of inputs.The robust optimization of flexible M6 wing illustrates that comparied with robust optimization results of DK，the drag coefficient of optimal result of SK has reduced 2.8 counts and the mean values in variable MachNumberrange have reduced 3.2 counts.The optimal result of SK has higher aerodynamic efficiency in design point and better drag divergence characteristics.It is manifested that stochastic surrogate model is favorable in robust optimizationand the SK surrogate model possesses high prediction accuracy.

aeroelasticity，computational fluid dynamics，deformation，design，drag coefficient，elastic deformation，finite element method，flexible wings，flow fields，flow charting，forecasting，genetic algorithms，geometry，Mach number，mean square error，Navier Stokes equations，optimization，pressure distributions，Reynolds numbers，statistics，stochastic models，structural dynamics，robust optimization static aeroelasticity；stochastic Kriging（SK）surrogate model

V211.3 V214.3+2

A

1000-2758（2015）06-0906-07

2015-03-31

國家“973”計劃（2014CB744804）資助

劉艷（1988—），西北工業大學博士研究生，主要從事氣動彈性分析與多學科優化設計研究。