基于狼爬山快速多智能體學習策略的電力系統智能發電控制方法

席磊余濤張孝順張澤宇譚敏

（華南理工大學電力學院廣州510641）

基于狼爬山快速多智能體學習策略的電力系統智能發電控制方法

席磊余濤張孝順張澤宇譚敏

（華南理工大學電力學院廣州510641）

為了解決互聯復雜電力系統環境下自動發電協調控制問題，提出了一種多智能體智能發電控制策略。提出了一種具有多步回溯及變學習率的多智能體新算法——“狼爬山”算法。該算法可根據據CPS標準求解各種復雜運行環境下的平均策略。基于混合策略及平均策略，此算法不僅在非馬爾可夫環境及大時延系統中具有高度適應性，而且能解決新能源電源接入所帶來的互聯復雜電力系統環境下自動發電協調控制問題。對標準兩區域負荷頻率控制電力系統模型及南網模型進行仿真，結果顯示該算法能獲得最優平均策略，閉環系統性能優異，與已有智能算法相比具有更高的學習能力及快速收斂速率。

智能發電控制狼爬山變學習率平均策略

3　引言

互聯電網自動發電控制（Automatic Generation Control，AGC）是電網能量管理系統的基本功能之一，是保證電力系統有功功率平衡和頻率穩定的基本手段［1-3］。研究模型一般是以經典的兩區域IEEE負荷頻率控制（Load-Frequency Control，LFC）為基礎的頻域線性模型，電力系統LFC問題同時也是控制理論界研究的一個經典問題，控制理論新方法也常會被引入到LFC問題中來，文獻［4］對半個世紀以來LFC在理論與技術研究中的進展進行了全面的回顧。為了計算區域發電速率，近兩年，歐美電力系統開始采用區域控制誤差（Area Control Error，ACE）差異互換（ACE Diversity Interchange，ADI）方法［5］。2000年以來，國內兩大電網公司開始采用北美電力可靠性委員會建議的CPS標準，以對所有控制區域進行協調。在智能電網發展的大背景下，開發具有自主學習能力和廠網協調能力的智能發電控制（Smart Generation Control，SGC）逐漸成為一種趨勢［6-8］。

近幾年來，多智能體強化學習算法已成為機器學習領域研究的熱點，特別是基于經典Q學習的算法框架體系得到了不斷充實和發展。文獻［9，10］已經用多個應用實例證明了多智能強化學習中的每個智能體能追蹤其他智能體的決策以動態協調自身動作。數種以博弈論為基礎，并用Q學習方法來實現的分布式強化學習方法被陸續提出，如Minimax-Q［11］、Nash-Q［12］和Friend-or-Foe Q［13］。然而由于Minimax_Q是零和博弈、Nash-Q占用空間大、FF-Q的Agent必須知道其他Agent是敵是友使得FF-Q只具有個體理性等缺陷，限制了這些算法的應用。文獻［14］提出了一種基于相關均衡的分布式多智能體學習算法——DCE Q（λ）算法，以解決互聯電網AGC協調控制問題，取得了較為滿意的控制效果。然而，當智能體數量增加時，DCE Q（λ）算法在搜索多智能體均衡解時間呈幾何數增加，限制了其方法在更大規模的電網系統中廣泛應用。文獻［15］于2002年開發了“贏”或“快速學習”的爬山策略算法（Win or Learn Fast Policy Hill-Climbing，WoLFPHC）。學習中，每個Agent采用混合策略，且只保存自身的Q值表。所以，一方面，它避免了一般Q學習中需要解決的探索和利用這一矛盾問題；另一方面，它可解決多Agent系統的異步決策問題。

本文融合了WoLF-PHC算法、資格跡［16］和SARSA算法［17］，提出了分布式WoLF-PHC（λ）算法，即Distributed WoLF-PHC（λ）（稱為“狼爬山”算法），并將該方法應用于求解多智能體SGC中的均衡解。標準兩區域負荷頻率控制的電力系統模型及南網模型的兩個實例研究證明了此算法的有效性。由于WoLF學習率隨環境適應性地變化，與其他SGC方法相比，狼爬山算法具有更高的快速收斂速率。

3　狼爬山算法

1.1Q（λ）學習

狼爬山算法可以基于Q學習和TD等強化學習算法。所提出的方法也是基于經典Q學習算法框架體系。Q學習算法是由文獻［18］提出的具有普遍性的強化學習算法，其中狀態動作對由值函數Q（s，a）進行評估。最優目標值函數Vπ*（s）及策略π*（s）為

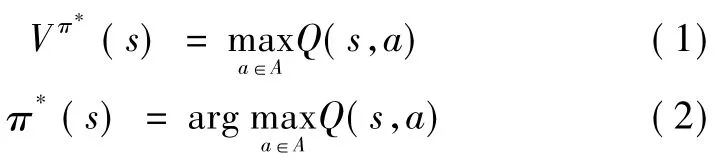
式中A為動作集。

資格跡（Eligibility Trace）詳細記錄各聯合動作策略發生的頻率，并依此對各動作策略的迭代Q值進行更新。在每次迭代過程中，聯合狀態與動作會被記錄到資格跡中，對于學習過程中多步歷史決策給予獎勵和懲罰。Q函數與資格跡以二維狀態動作對的形式被記錄下來。資格跡將歷史決策過程的頻度及漸新度聯系在一起，以獲得AGC控制器的最優Q函數。Q函數的多步信息更新機制是通過資格跡的后向評估來獲得。常用的資格跡算法有4種：TD（λ）［19］、SARSA（λ）［17］、Watkin's Q（λ）［18］和Peng's Q（λ）［16］。由于計算量的限制，選擇基于SARSA（λ）的資格跡

式中：ek（s，a）為在狀態s動作a下第k步迭代的資格跡；γ為折扣因子；λ為跡衰減因子。Q（λ）值函數的回溯更新規則利用資格跡來獲取控制器行為的頻度和漸新度兩種啟發信息。當前值函數誤差的評估分別由式（4）和式（5）計算。

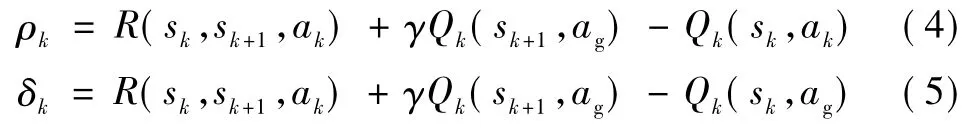
式中：R（sk，sk+1，ak）為在選定的動作ak下，狀態從sk到sk+1的智能體獎勵函數；ag為貪婪動作策略；ρk為智能體在第k步迭代過程中的Q函數誤差；δk為Q函數誤差的評估。Q函數更新為

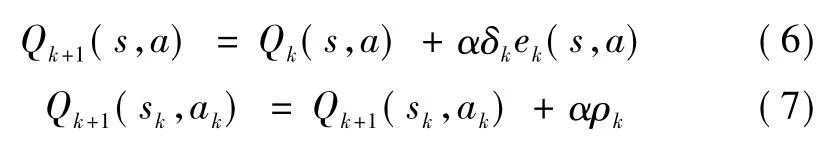
式中α為Q學習率。隨著充分的試錯迭代，狀態值函數Qk（s，a）能收斂到由具有概率1的Q*矩陣表示的最優聯合動作策略。

1.2狼爬山算法原理

1.2.1WoLF原理

學者們已經對具有啟發式方法的WoLF原理在對手問題上的應用進行了深入研究，失敗時加快學習速度，贏時降低學習速度［15］。和其他智能體當前策略相反的平均策略相比，如果一個游戲者更喜歡當前策略，或當前的期望獎勵比博弈的均衡值大，那么游戲者便贏了。然而文獻［15］對WoLF原理的游戲者所需要的知識給出了嚴格要求，這也限制了WoLF原理的普適性。

1.2.2PHC

爬山策略（Policy Hill-Climbing，PHC）算法是WoLF原理的擴展，以使其更具普適性，根據爬山策略算法，Q學習能獲得混合策略以及保存Q值。由于PHC具有理性及收斂特性，當其他智能體選擇固定策略時，它能獲得最優解。文獻［15］已經證明通過合適的探索策略，Q值會收斂到最優值Q*，并且通過貪婪策略Q*，U能獲得最優解。雖然此方法是理性且能獲得混合策略，但其收斂特性不明顯。

1.2.3WoLF-PHC

文獻［15］于2002年提出了具有變學習率φ的WoLF-PHC算法，與此同時滿足理性和收斂特性。兩個學習參數φlose和φwin用來表明智能體的贏與輸。WoLF-PHC是基于虛擬博弈，它能通過近似均衡的平均貪婪策略取代未知的均衡策略。

對于一個已知的智能體，基于混合策略集U（sk，ak），它會在狀態sk過渡到sk+1，且具有獎勵函數R的情況下執行探索動作ak，Q函數將根據式（6）和式（7）進行更新，U（sk，ak）的更新律為

式中φi為變學習率，且φlose＞φwin。如果平均混合策略值比當前的策略值低，則智能體贏了，選擇φwin，否則選擇φlose。它的更新律為

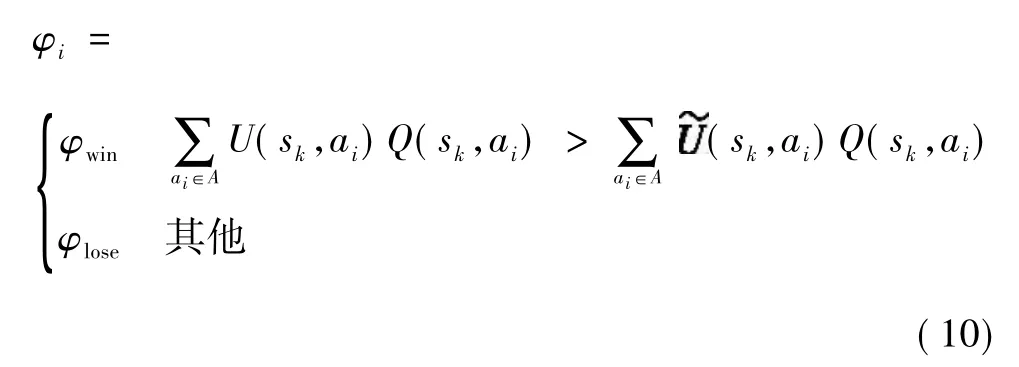
執行動作ak后，對sk狀態下所有動作的混合策略表進行更新

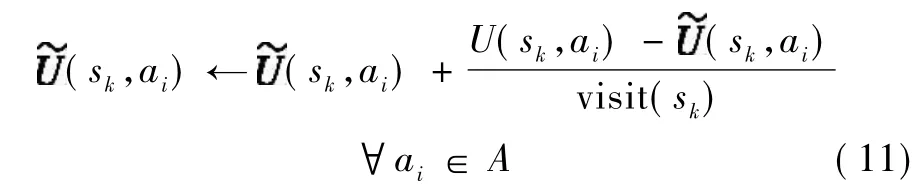
式中visit（sk）為從初始狀態到當前狀態所經歷的sk次數。

3　基于多智能強化學習的SGC設計

設計一種新穎的基于多智能強化學習的狼爬山算法，以尋求自適應協調的SGC。在每個迭代步，每個控制區域的狼爬山都將在線觀察當前的運行狀態以更新值函數和Q函數，然后執行一個基于平均混合策略的動作。設計包括獎勵函數的選擇、動作間隔的模糊化和參數設置等。

2.1獎勵函數的選擇

本文中智能控制器所追求的是CPS控制長期收益最大和盡可能避免頻繁大幅度升降調節功率兩個目標，獎勵函數中需綜合考慮這兩種指標的線性加權和。某i區域電網的評價獎勵函數Ri詳見文獻［14］。

2.2動作間隔的模糊化

動作區間模糊化能加快狼爬山算法收斂速度，避免不必要的學習。動作模糊化規則參見表1，表中各符號表示為負大（NB）、負中（NM）、負小（NS）、零（Z）、正小（PS）、正中（PM）和正大（PB）。

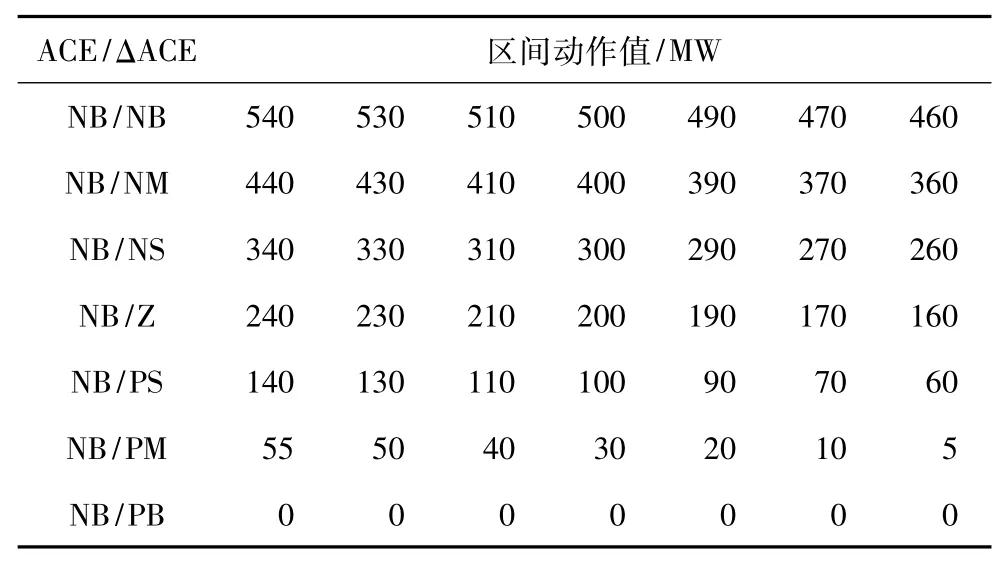
表1　動作模糊化部分具體規則Tab.1 Specific rule for the action fuzzification

實際應用中，需要規定各區域各自狀態、動作所代表符號的含義，并根據動作上下限確定區間動作數和各動作值。南網模型仿真實例中，動作區間模糊化共有49條規則，每條規則規定有7個離散動作，僅列取7條規則，如表1所示。表1中，最后一條規則NB/PB不需要學習即可判斷最優動作為0，因此動作空間均為0，NB、NM等輸入狀態符號的定義見表2。

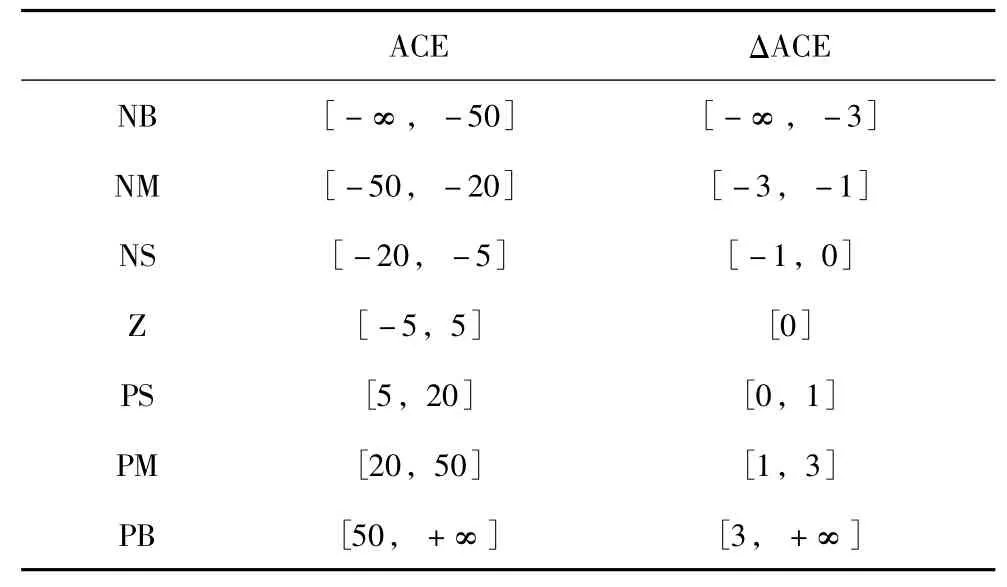
表2　動作模糊化ACE狀態劃分Tab.2 The fuzzy rules of the state division of ACE

2.3參數設置

如前文所述，控制系統的設計需要對4個參數λ、γ、α、和φ進行合理設置［15-17，20］。

資格跡衰減因子λ設置為0＜λ＜1，其作用是在狀態動作對間分配信譽。對于長時延系統，它影響收斂速度及非馬爾可夫效果。一般來說，回溯法中λ能被看作為時間標度因素。對于Q函數誤差來說，小的λ意味著很少的信譽被賦予到歷史狀態動作對，而大的λ表明分配到了更多的信譽。

折扣因子γ設置為0＜γ＜1，為Q函數將來的獎勵提供折扣。在以熱電廠為主導的LFC控制過程中，由于最新的獎勵最重要，所以應該選取近似1的值［20］。實驗證明0.6＜γ＜0.95具有更好的效果，選取γ=0.9。

Q學習率α設置為0＜α＜1，對Q函數的收斂速率即算法穩定性進行權衡。更大的α可以加快學習速度，而更小的α能提高系統的穩定性。在預學習過程中，我們選擇α的初始值為0.1，以獲得總體的探索［17］，然后為了逐漸提高系統的穩定性，它將以線性方式減少。

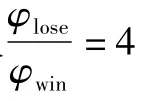
2.4狼爬山算法流程

狼爬山算法流程如圖1所示，嵌入了狼爬山算法的SGC控制器具有如下特性：①某一區域的控制策略僅在本區域有效；②在所有區域不能與此同時更新值函數Qk+1（s，a），因此對于所獲得的最優策略不可避免地產生了時延。

圖1　基于狼爬山的第i個智能體的SGC執行流程Fig.1 Execution steps of the DWoLF-PHC（λ）-based SGC for agent i

3　算例研究

3.1兩區域LFC電力系統

所提出的多智能體SGC策略已在兩區域LFC電力系統中進行了測試［20］，系統參數設置可參見文獻［21］。SCG的運行周期是3 s，且在二次調頻中具有20 s時延Ts。對于狼爬山來說，在最終的在線運行之前通過離線試錯而進行充分的預學習是必要的，包括在CPS狀態空間中的大量探索以優化Q函數和狀態值函數［22］。圖2為由一個連續10 min正弦擾動而產生的每個區域的預學習。由圖可發現狼爬山收斂到兩個區域都具有合格CPS1（CPS1的10 min平均值）和EAVE-10-min（ACE的10 min平均值）的最優策略。

然而使用一個2范數的Q矩陣‖Qik（s，a）-Qi（k-1）（s，a）‖2≤ζ（ζ為已知常量）作為最優策略預學習的終止標準［20］。圖3為預學習期間A區域Q函數差分的收斂結果。與DCE Q（λ）相比收斂速度提高了40%。

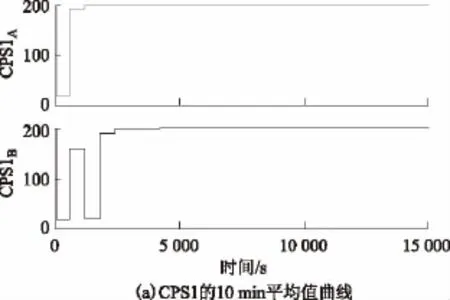
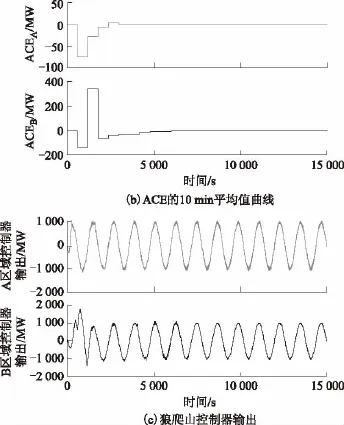
圖2　兩區域所獲得的狼爬山的預學習Fig.2 The pre-learning of DWoLF-PHC（λ）obtained in two area

圖3　預學習期間A區域Q函數差分的收斂結果Fig.3 Q-function differences convergence result obtained in area A during the pre-learning

為了評估算法的魯棒性，A區域在階躍負荷擾動下，對Q學習、Q（λ）學習、DCE Q（λ）和WoLF-PHC與狼爬山進行對比分析。對于狼爬山算法，在兩個區域中根據式（11）選擇相同的獎勵函數，權重因子選取為η1=1，η2=10，μ1=μ2=10。圖4a顯示它們的超調量分別為22.5%、18%、6%、2.5%和0%，并且它們的穩態時間分別為450 s、350 s、320 s、150 s和100 s，與DCE Q（λ）相比，狼爬山的收斂速度提高68%。圖4b和圖4c顯示CPS1和ACE的最小值也是狼爬山算法表現最佳。

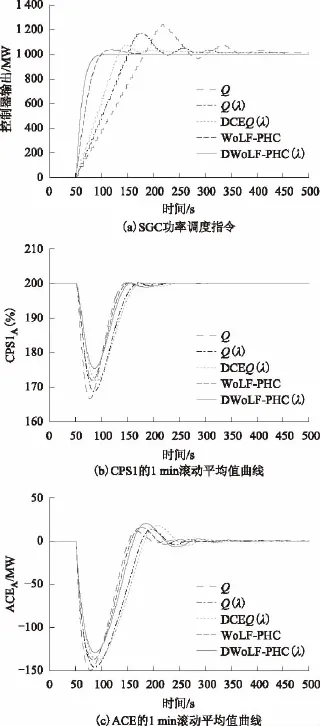
圖4　5種SGC控制器的控制性能對比圖Fig.4 Control performance obtained by five SGC controllers

表3列出了A、B區域不同的非馬爾可夫環境下每個算法的控制性能，選取具有不同二次調頻時延Ts及不同爬坡速率（Generation Rate Constraint，GRC）的8個火電機組進行測試。表中，Tc為預學習的平均收斂時間，ΔF和CPS1取預學習之后24 h的平均值，（CPS2）表示1 min ACE絕對值的平均值。由表3可看出，隨著Ts的變大Tc明顯增長，因此需要更多的迭代次數以獲得最優策略。然而，當Ts增加或GRC較少時，CPS指標僅輕微地弱化，因此火電占優的非馬爾可夫LFC問題可有效得到解決。

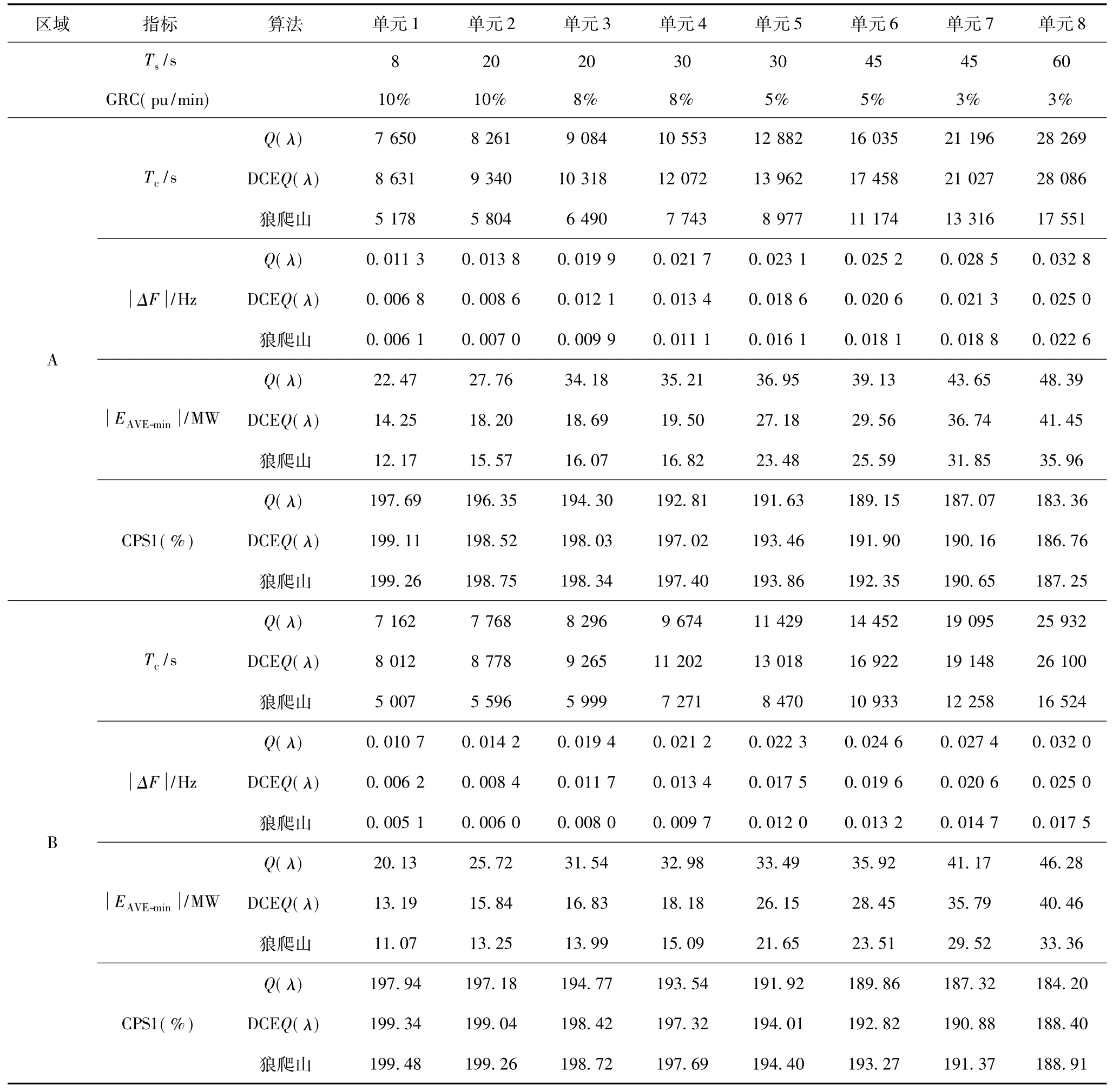
表3　不同時延所獲得的統計特性Tab.3 Statistic performances obtained under different time-delays

3.2南方電網模型

采用的南方電網四省區互聯負荷頻率響應模型可參見文獻［14，20，23，24］。通過超過30天的擾動統計實驗對多智能體SGC的長期性能進行評估。分別對4種控制器，即Q（λ）學習、R（λ）［22］學習、DCE Q（λ）和狼爬山進行測試。表4和表5分別列出了在標稱參數和擾動參數下所獲得的統計結果。

為了設計變學習率以獲得SGC協調，多智能體SGC提供了平均策略值。根據Tc、CPS值、順調次數、反調次數，從表4和表5可發現，狼爬山與其他算法相比具有更優的控制性能。

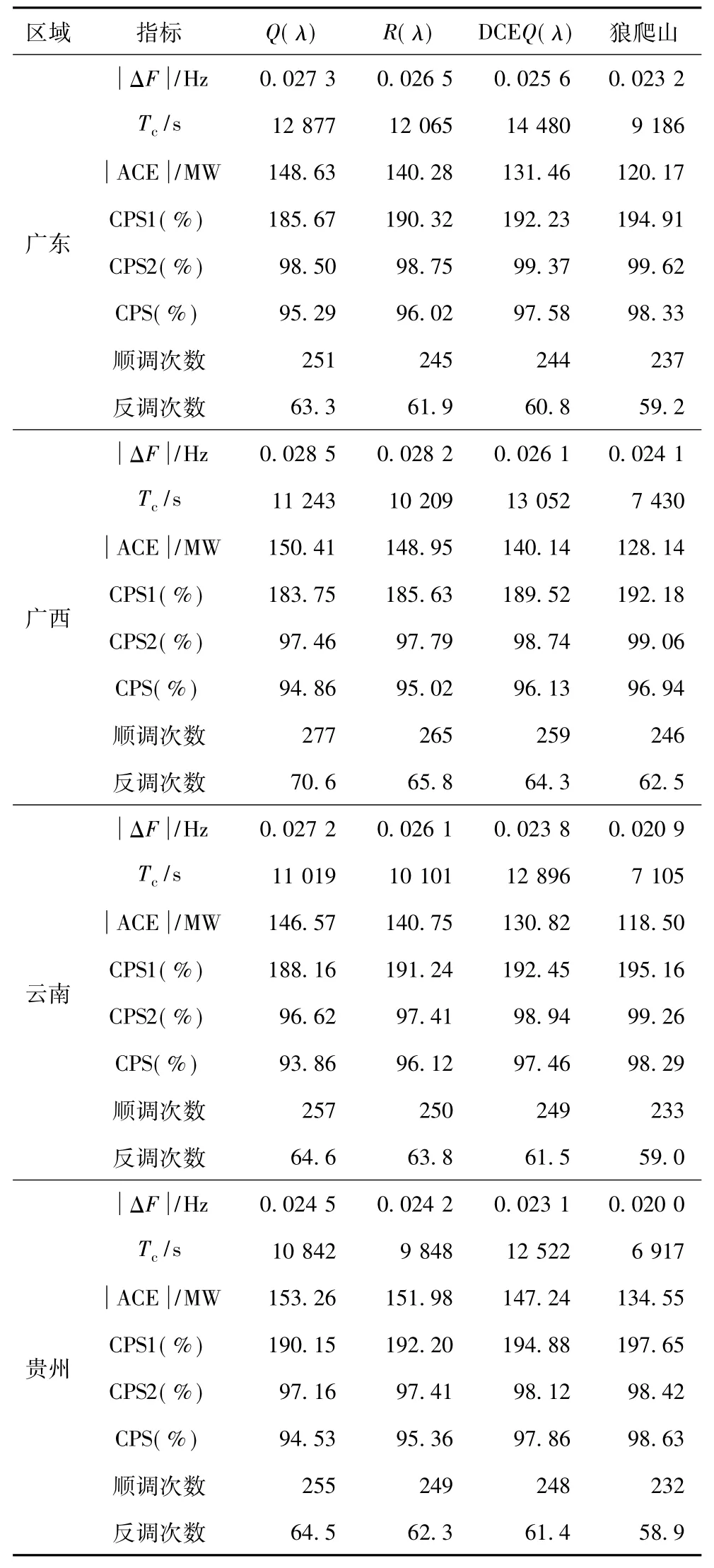
表4　南網模型在標稱參數下所獲得的統計性能Tab.4 Statistic experiment results obtained under the nominal parameter in the CSGmodel

3　結論

對于狼爬山算法，每個區域智能體不會減少與其他智能體之間的信息交換，而是時刻感知到其他智能體的動作引起的狀態變化。控制系統是多智能體系統，每個區域都嵌入了狼爬山算法，與DCE Q算法相比，看似Q學習一樣的單智能體算法，每個算法中都只有一個智能體，其他智能體動作會對當前的狀態及下一時刻狀態產生影響，這也就是所謂的智能體聯合動作，而智能體會隨狀態的變化而隨時變化學習率，這是狼爬山比Q學習優越的地方。事實上，如前言中所列舉的Minimax-Q、Nash-Q、Friend-or-Foe Q和DCE Q等多智能體學習算法本質上都是屬于多智能體之間的博弈，都可以歸納為納什均衡博弈。但不同于靜態博弈場景，對于屬于動態博弈的控制過程，納什均衡解在每個控制時間間隔的搜索速度并不一定都能滿足控制的實時性要求。所提出的狼爬山方法是通過平均策略取代多智能體動態博弈的均衡點求解，因此從博弈論的觀點來看，狼爬山方法可以看作是一種高效、獨立的自我博弈，降低了與其他智能體之間實時信息交換和聯合控制策略的求解難度。總的來說，主要貢獻如下：

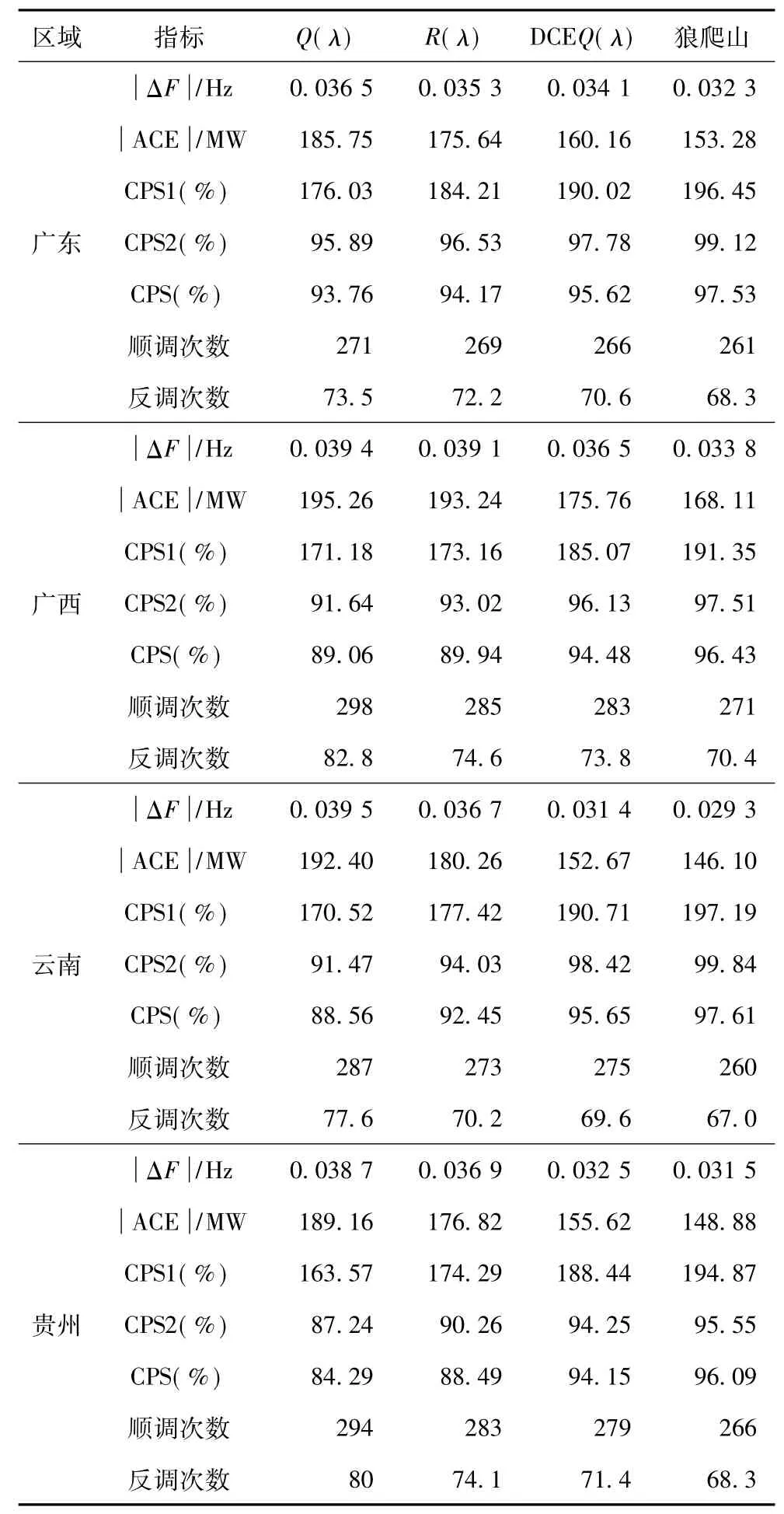
表5　南網模型在10%白噪聲參數下所獲得的統計性能Tab.5 Statistic experiment results obtained under a 10%white noise parameter perturbation in the CSGmodel

1）基于WoLF-PHC，融合SARSA（λ）和資格跡開發了一種新穎的狼爬山算法，能有效解決隨機博弈求解和在非馬爾可夫環境的應用問題。

2）通過隨機動態博弈的一種合適的贏輸標準，引入變學習率及平均策略以提高狼爬山動態性能。

3）基于標準兩區域負荷頻率控制電力系統模型及南網模型，對多種智能算法進行了SGC協調的仿真實例研究。仿真結果表明，與其他智能算法相比，狼爬山能夠獲得快速的收斂特性及學習效率，在多區域強隨機互聯復雜電網環境下具有高度適應性和魯棒性。

［1］溫步瀛.計及調速器死區影響的兩區域互聯電力系統AGC研究［J］.電工技術學報，2010，25（9）：176-182.

Wen Buying.Research on AGC of two-area interconnected power system considering the effect of the governor dead band［J］.Transactions of China Electrotechnical Society，2010，25（9）：176-182.

［2］付鵬武，周念成，王強鋼，等.基于時滯模型預測控制算法的網絡化AGC研究［J］.電工技術學報，2014，29（4）：188-195.

Fu Pengwu，Zhou Niancheng，Wang Qianggang，et al. Research on networked AGC system based on delay model predictive control algorithm［J］.Transactions of China Electrotechnical Society，2014，29（4）：188-195.

［3］趙旋宇.南方電網直調機組AGC研究［J］.電力系統保護與控制，2008，36（7）：54-58.

Zhao Xuanyu.Research on AGC for generations directly controlled by CSG［J］.Power System Protection and Control，2008，36（7）：54-58.

［4］Pandey S K，Mohanty S R，Kishor N.A literature survey on load-frequency control for conventional and distribution generation power systems［J］.Renewable and Sustainable Energy Reviews，2013，25（5）：318-334.

［5］Oneal A R.A simplemethod for improving control area performance：area control error（ACE）diversity interchange［J］.IEEE Transactions on Power Systems，1995，10（2）：1071-1076.

［6］杜貴和，王正風.智能電網調度一體化設計與研究［J］.電力系統保護與控制，2010，38（15）：127-131.

Du Guihe，Wang Zhengfeng.Design and research on power network dispatching integration of smart grid［J］. Power System Protection and Control，2010，38（15）：127-131.

［7］吳國沛，劉育權.智能配電網技術支持系統的研究與應用［J］.電力系統保護與控制，2010，38（21）：162-166，172.

Wu Guopei，Liu Yuquan.Research and application of technology support system for smart distribute grid［J］. Power System Protection and Control，2010，38（21）：162-166，172.

［8］尹明，王成山，葛旭波，等.中德風電發展的比較與分析［J］.電工技術學報，2010，25（9）：157-163.

Yin Ming，Wang Chengshan，Ge Xubo，et al. Comparison and analysis of wind power development between China and Germany［J］.Transactions of China Electrotechnical Society，2010，25（9）：157-163.

［9］Daneshfar F，Bevrani H.Load-frequency control：a GA-based multi-agent reinforcement learning［J］.IET Generation Transmission&Distribution，2010，4（1）：13-26.

［10］Bevrani H，Daneshfar F，Hiyama T.A new intelligent agent-based AGC design with real-time application［J］. IEEE Transactions on Systems，Man，and Cybernetics，Part C：Applications and Reviews，2012，42（6）：994-1002.

［11］Littman M.A generalized reinforcement-learningmodel：convergence and applications［C］.Proceedings of the 13th International Conference on Machine Learning，Bari，Italy，1996：310-318.

［12］Hu J，Wellman M P.Multiagent reinforcement learning：Theoretical framework and an algorithm［C］.Proceedings of 15th International Conference on Machine Learning，Madison，1999：242-250.

［13］Littman M L.Friend or foe Q-learning in general-sum Markov games［C］.Proceedings of the 18th International Conference on Machine Learning，Williamstown，Massachusetts，2001：322-328.

［14］Yu Tao，Xi Lei，Yang Bo，et al.Multi-agent stochastic dynamic game for smart generation control［J］.Journal of Energy Engineering，2015，DOI：10.1061/（ASCE）EY.1943-7897.0000275：04015012.

［15］Bowling M，Veloso M.Multiagent learning using a variable learning rate［J］.Artificial Intelligence，2002，136（2）：215-250.

［16］Peng Jing，Williams R J.Incremental multi-step Q-learning［J］.Machine Learning，1996，22（1-3）：283-290.

［17］Sutton R S，Barto A G.Reinforcement Learning：An Introduction［M］.Cambridge：MIT Press，1998.

［18］Watkins C J H，Dayan P.Q-learning［J］.Machine Learning，1992，8（3/4）：279-292.

［19］Sutton R S.Learning to predict by the methods of temporal differences［J］.Machine Learning，1988，3（1）：9-44.

［20］Yu T，Zhou B，Chan K W，et al.Stochastic optimal relaxed automatic generation control in Non-Markov environment based on multi-step Q（λ）learning［J］. IEEE Transactions on Power Systems，2011，26（3）：1272-1282.

［21］Elgerd O I.Electric Energy System Theory-An Introduction［M］.2nd ed.New York：McGraw-Hill，1982.

［22］Ernst D，Glavic M，Wehenkel L.Power systems stability control：reinforcement learning framework［J］. IEEE Transactions on Power Systems，2004，19（1）：427-435.

［23］Yu T，Zhou B，Chan K W，et al.R（λ）imitation learning for automatic generation control of interconnected power grids［J］.Automatica，2012，48（9）：2130-2136.

［24］Xi Lei，Yu Tao，Yang Bo，et al.A novelmulti-agent decentralized win or learn fast policy hill-climbing with eligibility trace algorithm for smart generation control of interconnected complex power grids［J］.Energy Conversion and Management，2015，103（10）：82-93.

A Fast M ulti-agent Learning Strategy Base on DW oLF-PHC（λ）for Smart Generation Control of Power System s

Xi Lei Yu Tao Zhang Xiaoshun Zhang Zeyu Tan Min
（School of Electric Power South China University of Technology Guangzhou 510641 China）

This paper proposes amulti-agent（MA）smart generation control scheme for the coordination of automatic generation control（AGC）in the power grid with system uncertainties.A novel MA new algorithm，i.e.DWoLF-PHC（λ）with a multi-step backtracking and a variable learning rate，is developed，which can effectively identify the optimal average policies under various operating conditions by the control performance standard（CPS）.Based on the mixed strategy and the average policy，the algorithm is highly adaptive in stochastic Non-Markov environments and large time-delay systems and can also achieve AGC coordination in interconnected complex power systems in the presence of increasing penetration of renewable energies.Simulation studies on both a two-area load-frequency control（LFC）power system and the China Southern Power Grid model have been done respectively.The results show that the algorithm can achieve the optimal average policies，the closed-loop system has excellent properties，and the algorithm has a fast convergence rate and a higher learning ability compared with other existing intelligentmethods.

Smart generation control，DWoLF-PHC（λ），variable learning rate，average policy

TM732

席磊男，1982年生，博士研究生，研究方向為電力系統優化運行與控制。（通信作者）

余濤男，1974年生，教授，博士生導師，研究方向為復雜電力系統的非線性控制理論和仿真。

國家自然科學基金（51177051、51477055）、國家重點基礎研究發展（973）計劃項目（2013CB228205）和廣東省綠色能源技術重點實驗室項目（2008A060301002）資助。

2015-01-05改稿日期2015-08-24