數字圖像處理課程中數學函數的形象化教學改革方法研究*

☆ 陳霄 陳玉忠鄧蕾蕾劉妍

（1.吉林農業大學信息技術學院，吉林長春 130118；2.吉林大學實驗室與設備管理處，吉林長春 130000；3.吉林藝術學院動漫學院吉林長春 130000）

數字圖像處理課程中數學函數的形象化教學改革方法研究*

☆ 陳霄1陳玉忠2鄧蕾蕾1劉妍3

（1.吉林農業大學信息技術學院，吉林長春 130118；2.吉林大學實驗室與設備管理處，吉林長春 130000；3.吉林藝術學院動漫學院吉林長春 130000）

數字圖像處理是一門理論與實踐并重的課程，課程與數學模型緊密相關，對于本科學生的學習是一個難點。針對數學模型不易理解這一問題，本文提出一種將數學模型形象化，圖像處理實例特殊化，實踐課程興趣化的教學模型。讓學生在更有效地理解數學模型的同時，可以更有效地運用圖像處理方法。

數字圖像處理；數學模型；形象化教學

一、引言

“數字圖像處理”是高等院校信息類專業的重要專業課程，也是與計算機視覺、模式識別、認知計算等研究相關的熱門學科。該課程希望通過對數字圖像處理基本理論的學習，建立學生對數字圖像處理學科的有效認知與興趣，通過實驗課強化數字圖像處理的編程能力，為學生未來就業從事圖像相關領域的工作奠定基礎。數字圖像處理課程涉及范圍廣，難度大，要求學生具有良好的數學和信號處理等相關知識的基礎，并且掌握一種編程語言［1，2］。同時，隨著近幾年計算機視覺的發展，圖像處理的新方法新思路更新迅速，如何更好地開展該課程教學，如何讓學生理解數字圖像處理并自主研究相關領域知識一直是專業課教師思考的問題。

二、課程特點及教學現狀

“數字圖像處理”課程是一門理論與實踐并重的課程，所涉及到的內容很豐富，課程中涉及的每個章節或每種算法都可以作為一個研究內容；該課程涉及計算機技術、數學物理、通信技術等知識，要求學生在前期學習中具有較好的相關知識基礎。

傳統“數字圖像處理”課程的教學存在以下問題：（1）開課時間過晚，高年級學生對課程了解少，缺乏興趣，并且對該課程不夠重視。（2）以往經驗認為該課程注重實踐，因此加大了實驗課教學環節，增加實驗課實踐，雖然學生得到一定程度提高，但總體學習還不夠理想［3］。

根據對學生的調查，部分學生認為課程晦澀難理解，老師講解的數學模型枯燥，不知道圖像處理中理論知識部分的作用，希望能夠更直接或者更實例化地講授該門課程。而講授課程的教師也很為難，該課程與數學理論知識緊密相連，沒有這些理論知識，很難真正理解該課程精髓，如果改成完全實例化教學，那可能與本科教學的目的不相符，只有更深入地了解課程中數學模型才可以更有效地利用，因此，僅僅以工程化舉例是不夠的。根據這一問題，我們采用數學模型形象化，圖像處理實例特殊化，實踐課程興趣化的教學模型。讓學生更有效地理解數學模型的同時，可以更有效地運用圖像處理方［4］。

三、改革的教學內容

1.形象化數學模型講授方法

學生們普遍反映數學模型晦澀，公式復雜很難理解。如小波變換，傅里葉變換，Gabor變換等都是數字圖像處理課程中重要的內容，也是課程的難點，這些數學變換模型復雜，學生不易理解。我們將復雜的數學變換公式轉化為數學模型，以形象化的方法將數學公式展示給學生。比如：在講解Gabor變換時，Gabor變換實質上是傅里葉變換的加窗函數，Gabor變化的定義式如下。

單從公式角度看，公式中參數多且難于理解，我們可以用圖形化方式向學生解釋什么是傅里葉變化的加窗函數。假設傅里葉函數如圖1所示。

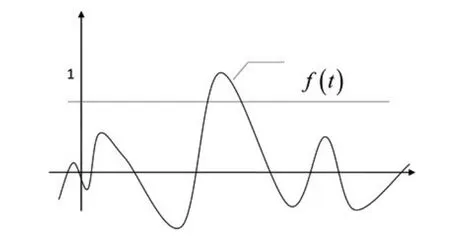
圖1 傅里葉變換

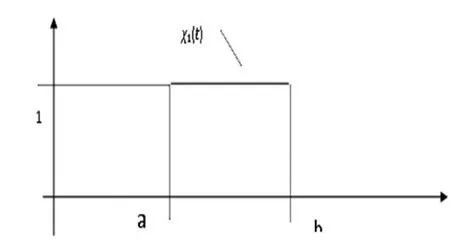
圖2 窗口函數

現在只想得到f（t）函數在區間［a.b］的部分，因此可以引入窗口，（如圖2）。有了傅里葉函數f（t）和窗口函數f（t），那么加窗的傅里葉函數就是兩個函數的乘積，表示為G（x）=x1（t）f（t），其形象化的數學表達形式如圖3所示。

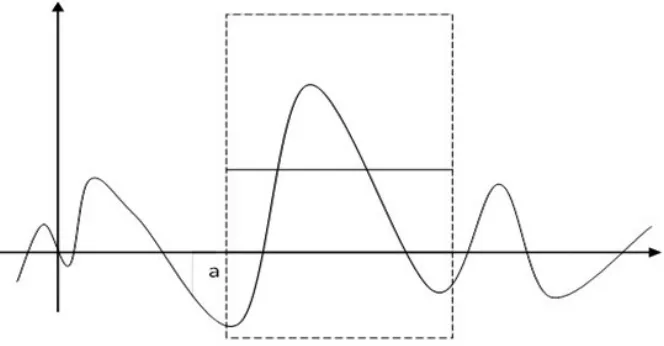
圖3 G（x）函數

其中，虛線框內得到的函數就是所說的傅里葉加窗函數，這樣再把窗口函數x1（t）換為高斯函數，就是我們通常所說的Gabor函數。這樣講解，學生在了解傅里葉變換和高斯變換的前提下，形象化地理解了Gabor變換。但是僅僅了解數學函數基本圖像還不夠，我們還要進一步讓學生理解函數。

2.多參函數變換的形象化教學

函數中必定存在著數學參數，而參數調節會對函數變化產生影響，因此，講解參數對函數變換的影響，可以進一步加深對函數的理解，同樣，利用2D-Gabor函數舉例。函數2D-Gabor的數學表達形式如下。

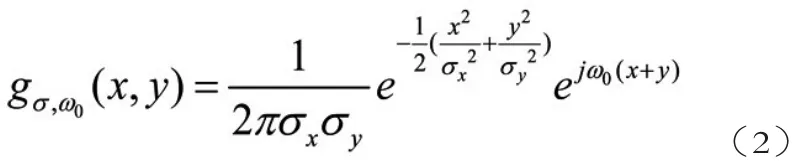
公式中參數較多，形式復雜，主要參數包括σx和σy，分別表示函數在x軸和y軸方向上的標準差，ω0表示空間頻率。這樣的講解較為晦澀。我們利用形象化的數學圖像解釋該函數與參數間的關系。

對于二維Gabor，參數變化引起圖像形狀的變化，不同參數的二維Gabor，在進行圖像特征提取時也會產生不同效果，針對該函數，通過調節某一參數，觀察二維Gabor圖像，以及特征提取結果的變化情況。二維Gabor核函數如下。

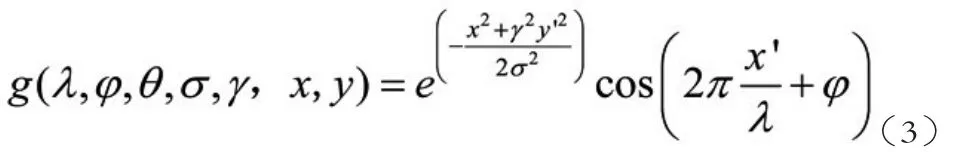
圖4 參數λ對圖像影響

如圖4所示，圖像中是波長分別為λ=5，λ=10的二維Gabor圖像，其他參數的值如下：方向0，相位偏移0，長寬比0.5。

除此以外，還有方向參數θ，相位參數φ，形狀參數γ，都采用通過調節參數，觀察數學函數相應的變化，最終對數學函數有一個較為深入的理解。

3.特殊實例的展示

本研究根據函數特點，選取特殊實例，實例可以選取極限狀態下的數字圖像，以突顯函數的作用，我們仍用二維Gabor函數為例，選取圖5中（a）等邊的八邊形進行實驗，此實例可以對檢驗二維Gabor對于紋理方向的敏感性（如圖5）。

圖5 2D-Gabor在不同方向的響應

圖5中（a）圖為實驗用的等邊8邊形，以下使用相同波長參數λ=8，不同方向的二維Gabor對圖5中（a）進行特征提取，從圖（b），（c），（d）和（e）中可以看出二維Gabor對紋理方向的響應敏感，圖5中（f）為θ=0°，θ=45°，θ=90°和θ=135°的四方向濾波圖像結果，可以看出基本上提取了六邊形的紋理，但是相對特征顯得有些粗糙；圖5中（g）是波長為λ=4，方向θ=0°，θ=30°，θ=60°，θ=90°，θ= 120°和θ=150°的6方向濾波特征提取結果。可以看出六邊形六方向濾波處理結果要比四方向效果要細致一些。

以此種方法，給予學生特殊實例圖像，啟發學生進一步思考：在調節相位參數φ后數字圖像處理效果會有什么變化，并作為實驗課內容讓學生完成，以更有效地讓學生理解數學模型中參數變化對圖像處理的影響。以上通過形象化的數學圖像解釋數學函數，通過參數調節進一步形象化理解函數本身，在選取特殊實例進一步說明數學函數的具體功能和函數對圖像變換產生的作用。這樣學生可以更深入理解數學函數。

4.相似數學模型的學習延伸性

在經過一輪詳細講解數學函數方法后，我們可以將此方法延伸到其他近似函數，如小波變換，K-L變換等。在學習數字圖像處理課程中關于數學函數的課程時，學生要知道這樣的學習思路：把復雜數學函數轉化為數學圖像，通過對參數調節理解數學函數，再例舉特殊實例了解數學變化在數字圖像處理過程中的功能作用。學生在了解此學習方法后，老師采取啟發驅動式的思想，讓學生主動學習。

5.以興趣和學校特點為導向教學和實踐方法

形象化的數學模型講解大大改善了數字圖像處理課程，但是興趣往往是學生重要的老師，因此我們在教學過程中注重興趣培養［5］。

（1）通過前沿性的圖像處理技術提高學生興趣。數字圖像處理是一門前沿科學，教材課程重點介紹常用算法，使學生掌握數字圖像處理原理。再結合國內外多種教材，精選本學科相關的中英文期刊，本區域特色相關的科研熱點項目等其他資料構建科學合理的教學內容和課程體系。教師將自己在科研中獲得的新理論、新技術、新方法、新成果及時引入到教學中，不斷充實和修正教學內容。通過一些發展中的、前沿性的算法著重介紹其思路和原理，教導學生注重思維培養而非局限于具體算法，培養學生的學習能力和創新思維。

（2）選取有效的實驗課內容：數字圖像的實用性很強，讓學生利用數字圖像處理方法解決一些與生活上相關的問題，例如：對植物葉子上的葉脈特征提取，多幅圖像拼接技術等來提高學生主動學習的積極性。同時，還要考慮學校科研大環境，吉林農業大學作為一個以農業為主的大學，在信息科學上也要結合農業，將數字圖像處理課程設計有效結合于農業科學，以農業為導向，完成數字圖像處理綜合應用。

四、結束語

數字圖像處理課程一直存在學生感覺難、聽課興趣不足，教師感覺累、教課不積極的問題。通過對數字圖像處理課程進行形象化教學方法，以貼近生活的實例為內容，通過前瞻性的科學知識吸引學生，并結合學校科研環境，有導向地設計課程實驗。促進科研的同時，更主要的是可以有效地提高學生對課程知識的掌握，促進學生對學習知識的綜合應用，使學生具有更好的創新能力。

［1］張書真，宋海龍.專題化教學模式在《數字圖像處理》課程中的實踐［J］.現代計算機，2011，（01）：54-56.

［2］李飛鵬，胡云峰.《數字圖像處理》實踐教學改革與效果分析［J］.中國科技信息，2010，（20）：258-259.

［3］賈永紅.數字圖像處理課程的建設與教學改革［D］.武漢：武漢大學，2007.

［4］饒俊慧.數字圖像處理課程教學改革探索［J］.中國科教創新導刊，2012，（10）：22-23.

［5］曹玉東，王冬霞，周軍.數字圖像處理課程教學改革與探索［J］.遼寧工業大學學報，2013，15（02）：129-134.

*吉林省教育科學“十二五”規劃課題（GB13180）。

G434

A

1671-7503（2015）05-0045-03

鄭方林］